一种相邻桩基水平动力相互作用分析方法及系统与流程

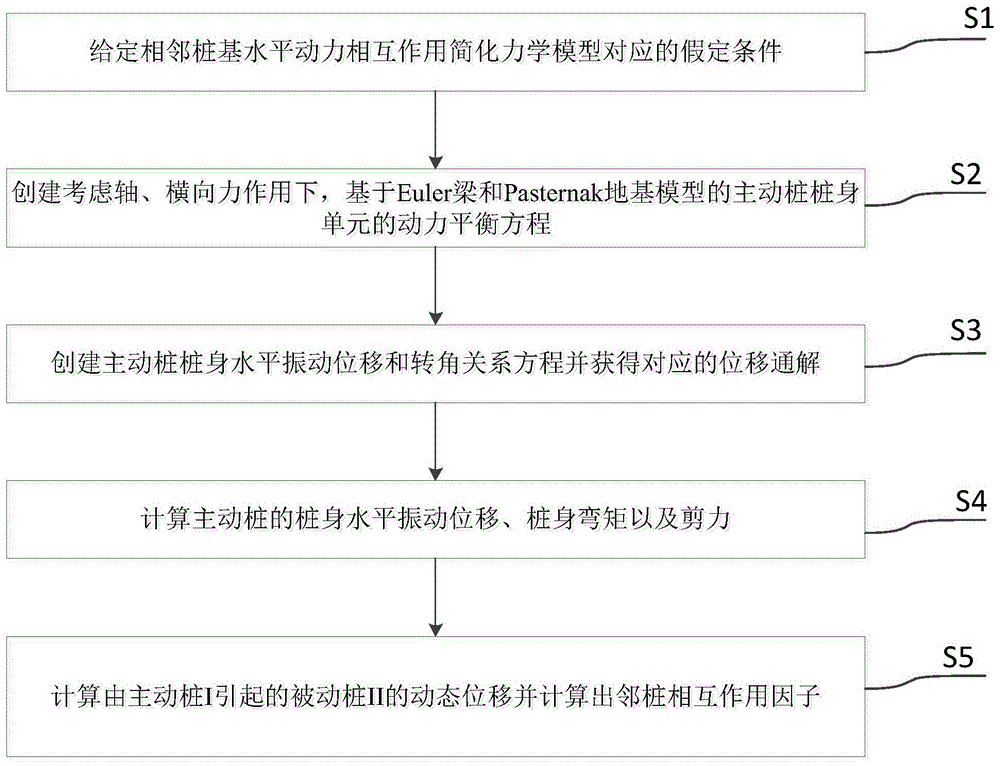
本发明涉及桩土水平振动技术领域，尤其涉及一种基于pasternak地基考虑轴向力作用下的相邻桩基水平动力相互作用分析方法及系统。

背景技术：

目前，在解决桩体水平振动动力响应问题时，为方便计算，桩周土体一般简化为winkler模型。但是winkler地基模型忽略了土的剪切效应，不能反映土体在纵向各层之间的连续性，使得计算结果在理论上不够严密。而pasternak地基模型在winkler模型的基础上考虑了地基土体剪切效应，使用pasternak地基模型使得桩土耦合系统能够更为合理的模拟实际工程工况。目前已有利用pasternak地基模型进行桩土水平振动的技术出现，但是该技术仅考虑单桩的桩体弯曲和剪切变形，虽然能够用于简谐激振力下桩体水平振动动力响应问题的求解，但是在实际工程中，桩基往往以群桩的形式出现。群桩在外界动荷载作用下会出现“群桩效应”，即某一桩受动荷载影响产生振动，其振动将使周围土体产生振动，振动波在土介质中传播进而对周围其他桩的振动产生影响，因此求解群桩动力问题时需考虑邻桩相互作用。且随着大型复杂建筑的兴起，基桩在复杂多向荷载同时作用下的受力分析也变得极为重要。

技术实现要素：

基于此，为解决现有所存在的不足，本发明专利基于pasternak地基提出一种考虑轴向力作用下的相邻桩基水平动力相互作用分析方法。

一种相邻桩基水平动力相互作用分析方法，其特征在于，包括如下步骤：

s1、给定相邻桩基水平动力相互作用简化力学模型对应的假定条件，所述假定条件至少包括：桩身被简化为圆形等截面、均质euler梁，设定桩周土体为均质土层，并将其简化为pasternak地基模型，设定所述模型各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；同时设定桩顶处仅发生水平位移，桩底处为固端约束；

s2、创建考虑轴、横向力作用下，基于euler梁和pasternak地基模型的主动桩桩身单元的动力平衡方程；

s3、创建主动桩桩身水平振动位移和转角关系方程并获得对应的位移通解；

s4、计算主动桩的桩身水平振动位移、桩身弯矩以及剪力；

s5、计算由主动桩i引起的被动桩ii的动态位移并计算出邻桩相互作用因子。

可选的，在其中一个实施例中，所述s2中的所述模型的创建过程包括：

建立主动桩的单桩水平振动模型桩身单元的动力平衡方程，所述动力平衡方程如下式：

式(1)中：为主动桩i桩身质点的水平位移；e^p、i^p、m^p分别为桩体弹性模量、截面惯性矩和单位长度质量，n0为作用在桩顶的轴向力；为桩周地基土剪切刚度；b0＝0.9(1.5d+0.5)为桩的计算宽度；

其中，和则按如下公式确定：

式中：为桩周土的剪切波速；e^s、ρ^s、β^s和υ^s分别为桩周土的弹性模量、密度、阻尼系数及泊松比；a0＝ωd/v^s为无量纲频率；t^s为地基土的剪切层厚度，t^s＝11d，d为桩径。

可选的，在其中一个实施例中，所述s3中的主动桩桩身水平振动位移和转角关系方程表示为：

u^p(z,t)＝u^p(z)e^iωt(5)

式中，u^p(z)为桩身质点水平位移幅值；

所述方程的通解的获取过程包括：

将式(5)分别代入式(1)，得到如下方程：

式中，w^p＝e^pi^p，j^p＝k'a^pg^p，

基于式(6)对应的4个特征根为则其方程位移通解为：

式(7)中，系数a11、b11、c11、d11的取值将由边界条件确定。

可选的，在其中一个实施例中，在所述s4中，基于euler梁理论，主动桩的桩身转角、弯矩、剪力与桩身水平位移相互关系为：

其中，式(9)、(10)和(11)中各个系数对应的表达式：

系数a12、a13、a14、b12、b13、b14、c12、c13、c14、d12、d13、d14由式(13)边界条件确定；

最后，基于上述主动桩的桩身转角、弯矩、剪力与桩身水平位移相互关系表达式计算主动桩的桩身水平振动位移、桩身弯矩以及剪力。

可选的，在其中一个实施例中，在所述s4中，系数a11、b11、c11、d11的求解过程包括如下步骤：

基于桩顶和桩底边界条件，具体边界条件如下式：

令f0(z)＝e^λzcosχz，f1(z)＝e^λzsinχz，f2(z)＝e^-λzcosχz，f3(z)＝e^-λzsinχz，f4＝λ³-3λχ²，f5＝3λ²χ-χ³并将上述表达式代入式(13)化简得：

式中：[x1]＝[a11b11c11d11]^t，l为桩长的变量形式；

对式(14)化简、整理得a11、b11、c11、d11的解析表达式如下：

式中：t＝χ(e^2λl-e^-2λl)+λ(2sin2χl)

同时，为便于后续分析，引入如下无量纲参数如下：

式中，umax(z)、mmax(z)、qmax(z)分别为桩基水平振动位移、弯矩和剪力最大值。

可选的，在其中一个实施例中，在所述s5中，计算由主动桩i引起的被动桩ii的动态位移的过程包括：

s51、假定主动桩i与被动桩ii中各桩的几何尺寸和材料性质均相同；

s52、基于土体水平位移的衰减函数，获取由主动桩i引起的场地振动位移，其中，土体水平位移的衰减函数为：

式(17)中：θ为两桩连线与振动方向x的夹角，s为两桩的间距；

对应的由主动桩i引起的场地振动位移为：

s53、考虑桩与土体之间的动力相互作用，被动桩ii的动力平衡方程为：

由于被动桩ii桩身内各单元水平位移和转角表示为

对式(19)进行化简进一步得到：

式中：式(20)方程的解由通解和特解两部分组成，其相应齐次方程的通解为：

式中：λ、χ的表达式a21、b21、c21、d21为待定系数；

式(20)的特解为：

式中：γ1＝λ+χi；γ2＝λ-χi

将式(22)代入式(20)分别求得：

则式(20)方程的解为：

s54、确定系数a21、b21、c21、d21，并计算被被动桩ii的位移，具体包括：

基于euler梁理论，被动桩ii桩身转角、弯矩、剪力与桩身水平位移相互关系为：

式中：

式(22)～式(24)中系数由边界条件确定，对应的表达式a22、b22、c22、d22、a23、b23、c23、d23、a24、b24、c24、d24为：

考虑边界条件桩顶约束转角，桩底固定端的情况，则所述边界条件为：

令f5＝f1+f3；f6＝f2+f4将被动桩ii桩身转角、弯矩、剪力与桩身水平位移相互关系表达式分别代入式(26)得：

式中：[x2]＝[a21b21c21d21]^t；

求解式(27)得未知变系数表达式a21、b21、c21、d21，并解得被动桩的位移。

可选的，在其中一个实施例中，在所述s5中，邻桩相互作用因子的计算公式为：

此外，为解决传统技术存在的不足，还提出了一种相邻桩基水平动力相互作用分析系统。

一种相邻桩基水平动力相互作用分析系统，其特征在于，包括：

第一数据获取单元，其用于给定相邻桩基水平动力相互作用简化力学模型对应的假定条件，所述假定条件至少包括：桩身被简化为圆形等截面、均质euler梁，设定桩周土体为均质土层，并将其简化为pasternak地基模型，设定所述模型各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；同时设定桩顶处仅发生水平位移，桩底处为固端约束；

第一模型创建单元，其用于创建考虑轴、横向力作用下，基于euler梁和pasternak地基模型的主动桩桩身单元的动力平衡方程；

第二模型创建单元，其用于创建主动桩桩身水平振动位移和转角关系方程并获得对应的位移通解；

第一数据获取单元，其用于计算主动桩的桩身水平振动位移、桩身弯矩以及剪力；

第二数据获取单元，其用于计算由主动桩i引起的被动桩ii的动态位移并计算出邻桩相互作用因子。

可选的，在其中一个实施例中，所述第一模型创建单元中的所述模型的创建过程包括：

建立主动桩的单桩水平振动模型桩身单元的动力平衡方程，所述动力平衡方程如下式：

式(1)中：为主动桩i桩身质点的水平位移；e^p、i^p、m^p分别为桩体弹性模量、截面惯性矩和单位长度质量，n0为作用在桩顶的轴向力；为桩周地基土剪切刚度；b0＝0.9(1.5d+0.5)为桩的计算宽度；

其中，和则按如下公式确定：

式中：为桩周土的剪切波速；e^s、ρ^s、β^s和υ^s分别为桩周土的弹性模量、密度、阻尼系数及泊松比；a0＝ωd/v^s为无量纲频率；t^s为地基土的剪切层厚度，t^s＝11d，d为桩径。

可选的，在其中一个实施例中，所述第二模型创建单元中的主动桩桩身水平振动位移和转角关系方程表示为：

u^p(z,t)＝u^p(z)e^iωt(5)

式中，u^p(z)为桩身质点水平位移幅值；

所述方程的通解的获取过程包括：

将式(5)分别代入式(1)，得到如下方程：

式中，w^p＝e^pi^p，

基于式(6)对应的4个特征根为则其方程位移通解为：

式(7)中，系数a11、b11、c11、d11的取值将由边界条件确定。

可选的，在其中一个实施例中，在所述s4中，基于euler梁理论，主动桩的桩身转角、弯矩、剪力与桩身水平位移相互关系为：

其中，式(9)、(10)和(11)中各个系数对应的表达式：

系数a12、a13、a14、b12、b13、b14、c12、c13、c14、d12、d13、d14由式(13)边界条件确定；

最后，基于上述主动桩的桩身转角、弯矩、剪力与桩身水平位移相互关系表达式计算主动桩的桩身水平振动位移、桩身弯矩以及剪力。

可选的，在其中一个实施例中，在所述第一数据获取单元中，系数a11、b11、c11、d11的求解过程包括如下步骤：

基于桩顶和桩底边界条件，具体边界条件如下式：

令f0(z)＝e^λzcosχz，f1(z)＝e^λzsinχz，f2(z)＝e^-λzcosχz，f3(z)＝e^-λzsinχz，f4＝λ³-3λχ²，f5＝3λ²χ-χ³并将上述表达式代入式(13)化简得：

式中：[x1]＝[a11b11c11d11]^t

对式(14)化简、整理得a11、b11、c11、d11的解析表达式如下：

式中：t＝χ(e^2λl-e^-2λl)+λ(2sin2χl)

同时，为便于后续分析，引入如下无量纲参数如下：

式中，umax(z)、mmax(z)、qmax(z)分别为桩基水平振动位移、弯矩和剪力最大值。

可选的，在其中一个实施例中，在所述第一数据获取单元中，计算由主动桩i引起的被动桩ii的动态位移的过程包括：

s51、假定主动桩i与被动桩ii中各桩的几何尺寸和材料性质均相同；

s52、基于土体水平位移的衰减函数，获取由主动桩i引起的场地振动位移，其中，土体水平位移的衰减函数为：

式(17)中：θ为两桩连线与振动方向x的夹角，s为两桩的间距；

对应的由主动桩i引起的场地振动位移为：

s53、考虑桩与土体之间的动力相互作用，被动桩ii的动力平衡方程为：

由于被动桩ii桩身内各单元水平位移和转角表示为

对式(19)进行化简进一步得到：

式中：式(20)方程的解由通解和特解两部分组成，其相应齐次方程的通解为：

式中：λ、χ的表达式a21、b21、c21、d21为待定系数；

式(20)的特解为：

式中：γ1＝λ+χi；γ2＝λ-χi

将式(22)代入式(20)分别求得：

则式(20)方程的解为：

s54、确定系数a21、b21、c21、d21，并计算被被动桩ii的位移，具体包括：

基于euler梁理论，被动桩ii桩身转角、弯矩、剪力与桩身水平位移相互关系为：

式中：

式(22)～式(24)中系数由边界条件确定，对应的表达式a22、b22、c22、d22、a23、b23、c23、d23、a24、b24、c24、d24为：

考虑边界条件桩顶约束转角，桩底固定端的情况，则所述边界条件为：

令f5＝f1+f3；f6＝f2+f4将被动桩ii桩身转角、弯矩、剪力与桩身水平位移相互关系表达式分别代入式(26)得：

式中：[x2]＝[a21b21c21d21]^t；

求解式(27)得未知变系数表达式a21、b21、c21、d21，并解得被动桩的位移。

可选的，在其中一个实施例中，在所述s5中，邻桩相互作用因子的计算公式为：

此外，为解决传统技术存在的不足，还提出了一种计算机可读存储介质，包括计算机指令，当所述计算机指令在计算机上运行时，使得计算机执行所述的方法。

实施本发明实施例，将具有如下有益效果：

本发明能够同时考虑轴向力作用下的相邻桩基水平动力相互作用，能适用于复杂多向荷载作用下的相邻桩基水平振动问题，可为桩基动力理论提供指导和参考作用。具体的，其其采用的pasternak地基模型考虑了桩周土体剪切效应，能更好的模拟桩周土体对桩身的约束作用；且同时考虑轴向力作用下的相邻桩基水平动力相互作用，能适用于复杂多向荷载作用下的相邻桩基水平振动问题，更符合实际工程中群桩相互作用体系的研究。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

其中：

图1为一个实施例中实施技术流程图；

图2为一个实施例中相邻桩基相互作用简化力学模型图；

图3为一个实施例中单桩简化计算模型图；

图4为一个实施例中双桩平面位置示意图。

图中：w、刚性基底。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

除非另有定义，本文所使用的所有的技术和科学术语与属于本发明的技术领域的技术人员通常理解的含义相同。本文中在本发明的说明书中所使用的术语只是为了描述具体的实施例的目的，不是旨在限制本发明。可以理解，本发明所使用的术语“第一”、“第二”等可在本文中用于描述各种元件，但这些元件不受这些术语限制。这些术语仅用于将第一个元件与另一个元件区分。举例来说，在不脱离本申请的范围的情况下，可以将第一元件称为第二元件，且类似地，可将第二元件为第一元件。第一元件和第二元件两者都是元件，但其不是同一元件。

鉴于现有技术并未考虑复杂多向荷载作用，且对于以往的桩土水平振动系统而言，因普遍采用的winkler地基模型忽略了土体的剪切效应，不能反映土体在纵向各层之间的连续性，使得计算结果在理论上不够严密。因此在本实施例中，特提出了一种基于pasternak地基提出的，考虑轴向力作用下的相邻桩基水平动力相互作用分析方法，主要是针对均质土中考虑轴向力作用下的相邻细长桩(即双桩)水平振动问题的求解，其通过考虑邻桩相互作用因子，并建立轴、横向力作用下基于pasternak地基模型的相邻桩基水平动力相互作用简化力学模型等技术，来解决复杂多向荷载作用下的相邻桩基水平振动问题，其中所述邻桩相互作用因子是指由于主动桩i受外荷载激振引起被动桩ii的附加动态位移与主动桩i在自身荷载作用下产生位移的比值。

具体的：如图1-4所示，一种相邻桩基水平动力相互作用分析方法，其特征在于，包括如下步骤：

s1、给定相邻桩基水平动力相互作用简化力学模型对应的假定条件，所述假定条件至少包括：桩身被简化为圆形等截面、均质euler梁，设定桩周土体为均质土层，并将其简化为pasternak地基模型(以描述桩-土相互作用)，设定桩-土模型内各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；同时设定桩顶处仅发生水平位移，桩底处为固端约束；

s2、创建考虑轴、横向力作用下，基于euler梁和pasternak地基模型的主动桩桩身单元的动力平衡方程；

s3、创建主动桩桩身水平振动位移和转角关系方程并获得对应的位移通解；

s4、计算主动桩的桩身水平振动位移、桩身弯矩以及剪力；

s5、计算由主动桩i引起的被动桩ii的动态位移并计算出邻桩相互作用因子。综上所述，本案所采用的pasternak地基模型在winkler模型的基础上考虑了地基土体剪切效应，使得桩土耦合系统能够更为合理的模拟实际工程工况；更重要的是本案同时考虑轴向力作用下的相邻桩基水平动力相互作用，即本案创建了pasternak地基模型+均质土体+考虑轴向力作用+双桩相互作用且细长桩基简化为euler梁模型的求解模式，以适用复杂多向荷载作用下的相邻桩基水平振动问题。

其中，在一些具体的实施例中，轴、横向力作用下基于pasternak地基模型的相邻桩即主动桩基i与被动桩基ii之间的水平动力相互作用简化力学模型示意图如图1所示，图中，和分别表示桩周土的刚度系数、阻尼系数和地基剪切系数，l和d分别表示桩长和桩径，同时由于主动桩i的桩顶受水平谐和激振力q0e^iωt和弯矩m0e^iωt的作用，则q0、m0分别为激振力幅值、弯矩幅值，ω为激振圆频率，t为时间。

在一些具体的实施例中，所述s2中轴、横向力作用下基于pasternak地基模型的细长单桩简化计算模型如图2所示，所述s2中的所述模型的创建过程包括：

综合euler梁和pasternak地基模型相关理论，建立主动桩的单桩水平振动模型桩身单元的动力平衡方程，所述动力平衡方程如下式：

式(1)中：为主动桩i桩身质点的水平位移；e^p、i^p、m^p分别为桩体弹性模量、截面惯性矩和单位长度质量，n0为作用在桩顶的轴向力；为桩周地基土剪切刚度；b0＝0.9(1.5d+0.5)为桩的计算宽度；在上述公式中，之所以设置是为了综合考虑了桩周土体剪切效应影响和桩顶轴力影响这两项因素对主动桩的单桩水平振动影响。

其中，和则按如下公式确定：

式中：为桩周土的剪切波速；e^s、ρ^s、β^s和υ^s分别为桩周土的弹性模量、密度、阻尼系数及泊松比；a0＝ωd/v^s为无量纲频率；t^s为地基土的剪切层厚度，t^s＝11d，d为桩径。

在一些具体的实施例中，所述s2中的主动桩桩身水平振动位移和转角关系方程表示为：

u^p(z,t)＝u^p(z)e^iωt(5)

式中，u^p(z)为桩身质点水平位移幅值；

所述方程的通解的获取过程包括：

将式(5)分别代入式(1)，得到如下方程：

式中，w^p＝e^pi^p，

式(6)为四阶线性常系数微分方程，则基于式(6)对应的4个特征根为则其方程位移通解为：

式(7)中，系数a11、b11、c11、d11的取值将由边界条件确定。

在其中一个具体实施例中，在所述s4中，基于euler梁理论，主动桩的桩身转角、弯矩、剪力与桩身水平位移相互关系为：

其中，式(9)、(10)和(11)中各个系数对应的表达式：

系数a12、a13、a14、b12、b13、b14、c12、c13、c14、d12、d13、d14由式(13)边界条件确定；

最后，基于上述主动桩的桩身转角、弯矩、剪力与桩身水平位移相互关系表达式计算主动桩的桩身水平振动位移、桩身弯矩以及剪力。

在其中一个更具体的实施例中，在所述s4中，系数a11、b11、c11、d11的求解过程包括如下步骤：

基于桩顶和桩底边界条件，具体边界条件如下式：

令f0(z)＝e^λzcosχz，f1(z)＝e^λzsinχz，f2(z)＝e^-λzcosχz，f3(z)＝e^-λzsinχz，f4＝λ³-3λχ²，f5＝3λ²χ-χ³并将上述位移、转角、弯矩和剪力的表表达式代入式(13)化简得：

式中：[x1]＝[a11b11c11d11]^t

对式(14)化简、整理得a11、b11、c11、d11的解析表达式如下：

式中：t＝χ(e^2λl-e^-2λl)+λ(2sin2χl)

将系数表达式(15)代入式(7)可求得桩身水平位移；根据桩身水平位移表达式，利用桩身弯矩、剪力与桩身水平位移之间的关系，可以求出桩身弯矩、剪力。

同时，为便于后续分析，引入如下无量纲参数如下：

式中，umax(z)、mmax(z)、qmax(z)分别为桩基水平振动位移、弯矩和剪力最大值。

在其中一个具体实施例中，在所述s5中，计算由主动桩i引起的被动桩ii的动态位移的过程包括：

s51、假定邻桩中各桩即主动桩i与被动桩ii中各桩的几何尺寸和材料性质均相同；上述分析得到主动桩i在简谐荷载作用下的水平动力响应解析解，下面进一步分析由于主动桩i引起被动桩ii的动态位移，两桩平面位置示意图如图3所示，两桩连线与振动方向x的夹角为θ，两桩的间距s。

s52、基于土体水平位移的衰减函数，获取由主动桩i引起的场地振动位移，其中，土体水平位移的衰减函数为：

式(17)中：θ为两桩连线与振动方向x的夹角，s为两桩的间距；

对应的由主动桩i引起的场地振动位移为：

s53、考虑桩与土体之间的动力相互作用，被动桩ii的动力平衡方程为：

由于被动桩ii桩身内各单元水平位移和转角表示为

对式(19)进行化简进一步得到：

式中：式(20)方程的解由通解和特解两部分组成，其相应齐次方程的通解为：

式中：λ、χ的表达式同前，a21、b21、c21、d21为待定系数；

式(20)的特解为：

式中：γ1＝λ+χi；γ2＝λ-χi

将式(22)代入式(20)分别求得：

则式(20)方程的解为：

s54、确定系数a21、b21、c21、d21，并计算被被动桩ii的位移，具体包括：

基于euler梁理论，被动桩ii桩身转角、弯矩、剪力与桩身水平位移相互关系为：

式中：

式(22)～式(24)中系数由边界条件确定，对应的表达式a22、b22、c22、d22、a23、b23、c23、d23、a24、b24、c24、d24为：

考虑边界条件桩顶约束转角，桩底固定端的情况，则所述边界条件为：

令f5＝f1+f3；f6＝f2+f4将被动桩ii桩身转角、弯矩、剪力与桩身水平位移相互关系表达式分别代入式(26)得：

式中：[x2]＝[a21b21c21d21]^t；

求解式(27)得未知变系数表达式a21、b21、c21、d21，并解得被动桩的位移进一步的，利用系数之间的关系式可进一步可求得被动桩转角及内力的表达式。

在其中一个具体实施例中，在所述s5中，邻桩相互作用因子的计算公式为：

基于相同的发明构思，本发明还提出了一种相邻桩基水平动力相互作用分析系统。

一种相邻桩基水平动力相互作用分析系统，其特征在于，包括：

第一数据获取单元，其用于给定相邻桩基水平动力相互作用简化力学模型对应的假定条件，所述假定条件至少包括：桩身被简化为圆形等截面、均质euler梁，设定桩周土体为均质土层，并将其简化为pasternak地基模型，设定所述模型各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；同时设定桩顶处仅发生水平位移，桩底处为固端约束；

第一模型创建单元，其用于创建考虑轴、横向力作用下，基于euler梁和pasternak地基模型的主动桩桩身单元的动力平衡方程；

第二模型创建单元，其用于创建主动桩桩身水平振动位移和转角关系方程并获得对应的位移通解；

第一数据获取单元，其用于计算主动桩的桩身水平振动位移、桩身弯矩以及剪力；

第二数据获取单元，其用于计算由主动桩i引起的被动桩ii的动态位移并计算出邻桩相互作用因子。

由于本系统的具体实施方案与上述方法的设计原理与方案一致，因此本处不再赘述。

基于相同的发明构思，本发明还提出了一种计算机可读存储介质，包括计算机指令，当所述计算机指令在计算机上运行时，使得计算机执行所述的方法。

以上所述实施例仅表达了本申请的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对本申请专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本申请构思的前提下，还可以做出若干变形和改进，这些都属于本申请的保护范围。因此，本申请专利的保护范围应以所附权利要求为准。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除