一种火箭动力定点着陆制导方法与流程

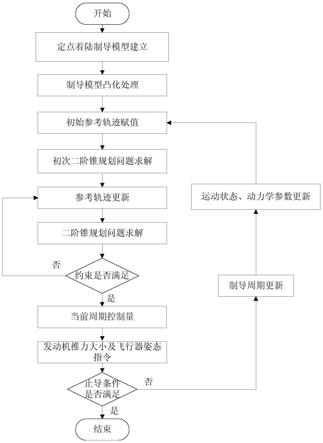
[0001]
本发明涉及一种火箭动力定点着陆方法，适合应用于运载火箭子级返回地球与定点垂直着陆任务，属于航天运输器制导、导航与控制技术领域。也可应用于月球及火星等地外天体定点软着陆任务，具有广阔的市场前景与应用价值。


背景技术：

[0002]
火箭动力定点软着陆制导方法是运载火箭再入返回与着陆控制系统方案设计的重要内容。目前，该方法的应用主要集中于地外天体着陆任务及近年来的商业火箭一子级垂直回收任务，如上世纪的阿波罗登月工程、近年来的美国火星科学实验室(mars science laboratory，msl)好奇号、洞察号火星着陆任务以及我国的嫦娥三号、嫦娥四号月面软着陆任务；另一方面，美国商业航天企业spacex与blue origin已经相继验证了火箭子级返回与垂直着陆制导技术的可行性，但由于商业利益，其均未公开其动力着陆制导方法细节。目前公开的应用于实际航天任务的火箭动力着陆制导的设计，第一代技术基于重力转弯制导，该方法局限于发动机推力不可调，能够实现垂直软着陆，但无法考虑终端位置及过程状态约束，着陆精度一般很低；第二代火箭动力着陆制导技术，基于e制导方法，在此算法框架内进行相应的改进，该方法通过设计多项式加速度剖面得到制导指令，制导律简单，计算效率高，但是不能满足诸如燃料、推力大小及方向、防地表碰撞等复杂强约束，该方法对偏差适应性有限，特别是对于火箭着陆任务而言，其剩余燃料有限，推力调节能力约束苛刻，气动等外部干扰更大，如何保证尽可能最省燃料的情况下安全着陆，对制导鲁棒性要求更高；近年来，随着星载或箭载计算机性能的提高，促使基于凸优化理论的第三代火箭动力着陆制导方法得到大量研究，其中的代表性方法g-fold(guidance for fuel-optimal large diverts)是美国jpl实验室针对下一代火星精确着陆任务提出的制导方法，其满足约束、燃料最优与自主在线的优良特性在xombie地面演示飞行器上得到了验证，可解决参数干扰大、动力反推段初始偏差大的难点；由于火星大气稀薄，特别在最终动力下降段，飞行速度已降到亚音速以下，气动力影响较小，因此g-fold制导方法将气动力作为干扰，在轨迹规划时未予以考虑。但对于地球返回着陆任务而言，由于地球密度是火星大气密度的一百倍左右，最终着陆段发动机反推点火时气动力影响显著，其影响不可忽略。
[0003]
现有的基于火箭动力的着陆制导方法，通常存在如下缺陷：
[0004]
1)考虑约束较少，在大偏差条件下无法实现定点着陆；
[0005]
2)无法有效考虑动力着陆过程中气动阻力对轨迹规划的影响；


技术实现要素：

[0006]
本发明的技术解决问题是：克服现有技术的不足，提出了一种火箭动力定点着陆制导方法，能满足火箭动力着陆中动力学、终端、过程状态及控制等复杂多约束，有效解决了发动机主推力与气动阻力协同作用下的定点着陆问题，提高了制导方案对燃料、初始状态和气动等不确定性的适应性，同时权衡了燃料最优性与制导鲁棒性，提高了返回安全性
与着陆控制精度。
[0007]
本发明的技术方案是：
[0008]
一种火箭动力定点着陆制导方法，包括步骤如下：
[0009]
1)在着陆目标点固联坐标系下建立定点着陆制导模型；
[0010]
2)将步骤1)建立的定点着陆制导模型凸化为二阶锥规划子问题模型；
[0011]
3)将无气动着陆问题的最优轨迹作为初始参考轨迹并赋值给步骤2)获得的二阶锥规划问题模型，利用内点法对步骤2)获得的二阶锥规划问题模型进行初次求解，判定求解结果是否收敛，若不收敛则调整二阶锥规划问题模型中的控制余量区间，直至求解结果收敛，获得对应的参考轨迹变量；
[0012]
4)更新参考轨迹变量
[0013]
将步骤3)获得的参考轨迹变量，作为输入量，利用内点法对步骤2)获得的二阶锥规划问题模型进行求解，判定求解结果是否收敛，若不收敛则调整二阶锥规划问题模型中的控制余量区间，直至求解结果收敛，获得更新后的参考轨迹变量；
[0014]
5)判断步骤4)更新后的参考轨迹变量，是否满足着陆约束条件，若满足，则进入步骤6)；若不满足，则返回步骤4)继续更新参考轨迹变量，直至满足着陆约束条件后进入步骤6)；所述着陆约束条件包括：着陆飞行器的推力大小约束、推力指向约束、终端位置约束及终端速度约束；
[0015]
6)根据满足着陆约束条件的参考轨迹变量，获得参考轨迹变量对应的推力矢量，确定着陆飞行器发动机的推力幅值与着陆飞行器的姿态角指令，并作为当前周期制导指令发送给着陆飞行器发动机推力调节器及姿态控制系统，然后进入步骤7)；
[0016]
7)判断当前周期着陆飞行器高度是否低于目标点高度，若满足，则结束着陆飞行器制导工作；若不满足，则进入步骤8)；
[0017]
8)更新制导周期，根据飞行器当前的运动状态及在线辨识的动力学参数，更新二阶锥规划子问题模型参数，将上个制导周期确定的参考轨迹变量作为新制导周期的初始参考轨迹变量，并返回步骤3)。
[0018]
步骤1)所述的定点着陆制导模型中含地球自转和气动阻力的动力学约束，具体如下：
[0019][0020]
其中，g＝[0,-g
0
,0]为常值引力加速度矢量，g
0
为地球表面重力加速度大小，t(t)为当前时刻火箭发动机推力矢量，m(t)为着陆飞行器当前的质量，ω为着陆天体自转角速度矢量，r(t)为着陆飞行器当前的位置矢量，v(t)为着陆飞行器当前的速度矢量，s
ref
为着陆飞行器有效横截面积，c
d
为气动阻力系数，ρ为大气密度，||v(t)||为着陆飞行器当前的速度矢量的模值。
[0021]
所述控制余量区间满足条件如下：t
min
+ρ
1
≤γ(t)≤t
max-ρ
2
[0022]
其中，t
min
为着陆飞行器的推力最小值，t
max
为着陆飞行器的推力最大值，ρ
1
的取值范围为0～10％t
min
，ρ
2
的取值范围为0～15％t
max
；γ(t)为引入的松弛因子，表示一维标量。
[0023]
步骤2)所述将定点着陆制导模型凸化为二阶锥规划子问题模型的方法，具体为：
[0024]
21)将推力大小约束t
min
≤||t(t)||≤t
max
转化为：
[0025]
||t(t)||≤γ(t)
[0026]
t
min
+ρ
1
≤γ(t)≤t
max-ρ
2
[0027]
其中，||t(t)||为发动机推力矢量的幅值大小；
[0028]
22)引入变量z(t)＝lnm(t),将21)中的约束进一步转化为：
[0029][0030]
其中，z
0
＝ln(m
0-αt
max
t)，α＝1/(i
sp
g
0
)，m
0
为着陆飞行器初始质量，t
0
为着陆初始时刻，i
sp
为飞行器火箭发动机比冲。
[0031]
步骤4)所述求解的二阶锥规划问题模型中含气动力项等式约束，具体为：
[0032][0033][0034]
其中，z
(i-1)
(t)、ρ
(i-1)
、v
(i-1)
(t)为步骤3)第i-1次获得的参考轨迹变量，分别为质量的自然对数、大气密度及速度矢量，i表示参考轨迹当前的更新次数，i为正整数。
[0035]
本发明与现有技术相比具有如下有益效果：
[0036]
1)本发明构建了含动力学、终端、过程状态及控制多约束的定点着陆问题，充分考虑了地球着陆任务中气动阻力带来的动力学非凸性影响，全面考虑了着陆过程相对导航敏感器视场、推力调节范围及调节速率约束等，满足了定点着陆工程约束；
[0037]
2)本发明将无损松弛与序列近似技术进行了有机结合，通过变量替换将原强非线性系统转化为控制仿射型系统，提升了问题的收敛性；
[0038]
3)本发明采用了基于控制余量的可行集边界裁剪策略，在干扰小时保留较多控制余量，牺牲掉部分最优性，在干扰大时释放控制余量，有效权衡了燃料最优性与制导鲁棒性，提升了着陆安全性。
附图说明
[0039]
图1为本发明的实现流程图。
具体实施方式
[0040]
本发明提供的一种火箭动力定点着陆制导方法，其实现步骤为：根据当前状态参数、飞行器参数及环境参数建立多约束火箭动力定点着陆轨迹规划最优控制模型，包含着陆终端位置、速度、姿态，飞行过程中防地表碰撞及燃料、推力大小及指向等复杂强约束，在动力学模型中考虑强非线性气动阻力带来的影响；引入控制余量调整策略，对原控制约束
进行调整；通过控制约束无损松弛以及变量替换构造控制仿射型系统；引入信赖域约束，将原动力学中非线性项进行序列线性化近似，将得到的线性最优控制系统进行离散化进一步转化为有限维参数优化问题；运用内点法快速高效求解转化所得的二阶锥规划问题，若无可行解，则进一步释放控制余量，直到迭代收敛至可行解即完成了推力矢量制导指令的计算。
[0041]
本发明一种火箭动力定点着陆制导方法，包括步骤如下：
[0042]
1)在着陆目标点固联坐标系下建立含动力学、终端状态、过程状态及控制多约束的定点着陆制导模型；
[0043]
2)将步骤1)建立的定点着陆制导模型凸化为二阶锥规划子问题模型；
[0044]
3)将无气动着陆问题的最优轨迹作为初始参考轨迹并赋值给步骤2)获得的二阶锥规划问题模型，利用内点法对步骤2)获得的二阶锥规划问题模型进行初次求解，判定求解结果是否收敛，若不收敛则调整二阶锥规划问题模型中的控制余量区间，直至求解结果收敛，获得对应的参考轨迹变量；
[0045]
4)更新参考轨迹变量
[0046]
将步骤3)获得的参考轨迹变量，作为输入量，利用内点法对步骤2)获得的二阶锥规划问题模型进行求解，判定求解结果是否收敛，若不收敛则调整二阶锥规划问题模型中的控制余量区间，直至求解结果收敛，获得更新后的参考轨迹变量；
[0047]
5)判断步骤4)更新后的参考轨迹变量，是否满足着陆约束条件，若满足，则进入步骤6)；若不满足，则返回步骤4)继续更新参考轨迹变量，直至满足着陆约束条件后进入步骤6)；所述着陆约束条件包括：着陆飞行器的推力大小约束、推力指向约束、终端位置约束及终端速度约束；
[0048]
6)根据满足着陆约束条件的参考轨迹变量，获得参考轨迹变量对应的推力矢量，确定着陆飞行器发动机的推力幅值与着陆飞行器的姿态角指令，并作为当前周期制导指令发送给着陆飞行器发动机推力调节器及姿态控制系统，然后进入步骤7)；
[0049]
7)判断当前周期着陆飞行器高度是否低于目标点高度，若满足，则结束着陆飞行器制导工作；若不满足，则进入步骤8)；
[0050]
8)更新制导周期，根据飞行器当前的运动状态及在线辨识的动力学参数，更新二阶锥规划子问题模型参数，将上个制导周期确定的参考轨迹变量作为新制导周期的初始参考轨迹变量，并返回步骤3)；
[0051]
步骤1)所述的定点着陆制导模型中含地球自转和气动阻力的动力学约束，具体如下：
[0052][0053]
其中，g＝[0,-g
0
,0]为常值引力加速度矢量，g
0
为地球表面重力加速度大小，t(t)为当前时刻火箭发动机推力矢量，m(t)为着陆飞行器当前的质量，ω为着陆天体自转角速度矢量，r(t)为着陆飞行器当前的位置矢量，v(t)为着陆飞行器当前的速度矢量，s
ref
为着陆飞行器有效横截面积，c
d
为气动阻力系数，ρ为大气密度，||v(t)||为着陆飞行器当前的速度矢量的模值。
[0054]
步骤3)与步骤4)中所述控制余量区间满足条件如下：
[0055]
t
min
+ρ
1
≤γ(t)≤t
max-ρ
2
[0056]
其中，t
min
为着陆飞行器的推力最小值，t
max
为着陆飞行器的推力最大值，ρ
1
、ρ
2
为控制余量调整值。ρ
1
的取值范围为0～10％t
min
，ρ
2
的取值范围为0～15％t
max
；γ(t)为引入的松弛因子，表示一维标量。
[0057]
步骤2)所述将定点着陆制导模型凸化为二阶锥规划子问题模型的方法，具体为：
[0058]
21)将推力大小约束t
min
≤||t(t)||≤t
max
转化为：
[0059]
||t(t)||≤γ(t)
[0060]
t
min
+ρ
1
≤γ(t)≤t
max-ρ
2
[0061]
其中，||t(t)||为发动机推力矢量的幅值大小；
[0062]
22)引入变量z(t)＝lnm(t),将21)中的约束进一步转化为：
[0063][0064]
其中，z
0
＝ln(m
0-αt
max
t)，α＝1/(i
sp
g
0
)，m
0
为着陆飞行器初始质量，t
0
为着陆初始时刻，i
sp
为飞行器火箭发动机比冲。
[0065]
步骤4)所述求解的二阶锥规划问题模型中含气动力项等式约束，具体为：
[0066][0067][0068]
其中，z
(i-1)
(t)、ρ
(i-1)
、v
(i-1)
(t)为步骤3)第i-1次获得的参考轨迹变量，分别为质量的自然对数、大气密度及速度矢量，i表示参考轨迹当前的更新次数，i为正整数。
[0069]
实施例
[0070]
本实施例提供了一种火箭动力定点着陆制导方法，如图1所示，具体实现如下：
[0071]
第一步，输入当前状态参数、飞行器参数、环境参数
[0072]
1)针对基于火箭动力的着陆飞行器，根据当前飞行器位置、速度、剩余燃料及主发动机比冲与推力调节参数等输入，计算飞行时间可行域
[0073][0074]
其中，||v(t)||为当前速度大小，m
dry
为着陆飞行器结构质量，m
fuel
为着陆当前剩余燃料，t
min
、t
max
为发动机推力大小调节上下限，ρ
1
、ρ
2
为控制余量调整值，α＝1/(i
sp
g
0
)，i
sp
为发动机比冲，g
0
为着陆天体地表引力加速度大小。
[0075]
2)确定制导目标与制导启动迭代初始值。
[0076]
对于地球返回任务而言，若在陆上着陆，着陆场可事先选定，若在海上着陆，可根据当前燃料与火箭返回状态，调整海上着陆船舶抵达火箭最优着陆区域；对于地外天体还需要通过障碍识别在线选出符合燃料及过程约束的可达目标区域，制导目标确定后，可通
过求解无气动着陆问题的最优解作为原始定点着陆问题的迭代求解的初始参考轨迹。
[0077]
第二步，构建含动力学、终端、过程状态及控制多约束的定点着陆问题
[0078]
根据步骤一中确定的着陆目标点，确定着陆目标点固联坐标系，在此坐标系中构造定点着陆问题，该问题包含以下结构：火箭动力与气动阻力共同作用下的动力学非凸约束，着陆位置、速度与姿态终端等式约束，可用推进剂不等式线性约束，着陆过程相对导航敏感器视场、地表防碰撞不等式二阶锥约束，以及推力调节范围及调节速率不等式非凸约束，以燃料最省为最优性能指标。
[0079][0080]
s,t.
[0081][0082][0083][0084]
0<t
min
≤||t(t)||≤t
max
[0085][0086]
r(0)＝r
0
,v(0)＝v
0
,m
0
(0)＝m
0
[0087]
r(t
f
)＝r
f
,v(t
f
)＝0
[0088][0089]
m(t
f
)≥m
dry
[0090]
||[r
y
(t),r
z
(t)]
t
||tanθ
gs
≤r
x
(t)
[0091][0092]
式中，r(t),v(t),m(t)为着陆飞行器当前的位置速度矢量和质量，t(t)为当前时刻火箭发动机推力矢量，g为常值引力加速度矢量，α＝1/(i
sp
g
0
)中i
sp
为发动机比冲，c
d
为气动阻力系数，ω为着陆天体自转角速度矢量，t
min
、t
max
为发动机推力大小调节上下限，为发动机允许最大推力调节速率。
[0093]
令x＝[r,v,m]
t
，u＝t，进一步对其约束进行整理，可将此问题结构归一化为
[0094][0095]
上述式中为非线性动力学约束，x(0)＝x
0
,x(t
f
),u(t
f
)∈υ为初始、终端位置速度及终端着陆姿态约束，为线性等式约束，0<t
min
≤||u(t)||≤t
max
、为控制非凸约束，l(t,x)≤0及f(t,u,||u||)≤0为原问题过程状态及控制变量线性或二阶锥不等式约束。
[0096]
第三步，进行控制余量调整
[0097]
为了应对实际飞行过程中动力学与环境参数的不确定性，对原着陆问题的控制约束可行集进行调整，即在制导启动初始阶段将控制变量不等式约束加强，牺牲一定的最优性，同时最大限度利用气动力进行减速，着陆后期，气动力出现大偏差状态时，可行解不存在时，释放出控制余量，按照原最大控制能力边界进行实时轨迹规划，可行集剪裁需在原始问题控制约束上进行，如下
[0098]
0<t
min
+ρ
1
≤||u(t)||≤t
max-ρ
2
ꢀꢀꢀꢀꢀꢀ
(4)
[0099]
第四步，将步骤二建立的定点着陆制导模型凸化为二阶锥规划子问题模型；
[0100]
41)根据步骤三中控制余量调整后的控制变量不等式约束，存在推力下限不为零的非凸约束，引入松弛因子进而得到||u(t)||≤γ(t)，并引入新的线性不等式约束
[0101]
0<t
min
+ρ
1
≤γ(t)≤t
max-ρ
2
ꢀꢀꢀꢀꢀꢀ
(5)
[0102]
42)在41)基础上引入变量
[0103][0104]
松弛因子约束转化为
[0105][0106]
其中z
0
＝ln(m
0-αt
max
t)；同时，将推力调节变化率离散为前后拍推力变化约束||t(t
k+1
)||-||t(t
k
)||≤δt
m
，δt
m
为推力幅值前后拍最大允许变化量，引入变量后进一步转化为
[0107][0108]
其中，δt
k
为离散后为前后两拍时间间隔。
[0109]
43)通过上述步骤，原定点着陆非线性动力学系统转化为了控制仿射型系统
[0110][0111]
其中，b
c
为常值控制矩阵，为转化后线性或二阶锥的状态及控制不等式约束。
[0112]
44)进行动力学非凸约束序列近似、离散化构造有限维参数优化问题
[0113]
利用步骤四中得到的控制仿射型问题结构，在步骤一中确定的初始轨迹基础上进行序列线性化近似
[0114][0115]
其中。
[0116]
同时引入信赖域约束，以保证问题的收敛性
[0117][0118]
最终消除掉了气动阻力加速度带来的强非线性，构造得到了连续最优控制问题，其状态与控制约束均为凸约束，该问题结构为
[0119][0120]
然后利用步骤一中确定的飞行时间可行域，确定轨迹离散点选取，将线性连续动态系统转化为有限维参数优化问题。
[0121]
第五步，基于内点法进行二阶锥规划问题求解
[0122]
51)利用内点法求解步骤五中转化得到的序列二阶锥规划问题，在信赖域约束下迭代求解，直至满足收敛条件，即前后迭代轨迹参数误差小于设定值。
[0123]
52)在步骤一中确定的飞行时间可行域内利用黄金搜索策略找到最优飞行轨迹。
[0124]
第六步，根据满足着陆约束条件的参考轨迹变量，获得参考轨迹变量对应的推力矢量，确定着陆飞行器发动机的推力幅值与着陆飞行器的姿态角指令，并作为当前周期制导指令发送给着陆飞行器发动机推力调节器及姿态控制系统，然后进入步骤七；
[0125]
第七步，判断当前周期着陆飞行器高度是否低于目标点高度，若满足，则结束着陆飞行器制导工作；若不满足，则进入步骤八；
[0126]
第八步，更新制导周期，根据飞行器当前的运动状态及在线辨识的动力学参数，更新二阶锥规划子问题模型参数，将上个制导周期确定的参考轨迹变量作为新制导周期的初始参考轨迹变量，并返回步骤三。
[0127]
本发明说明书中未作详细描述的内容属本领域技术人员的公知技术。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除