一种基于预测控制的高速列车节能运行曲线在线计算方法与流程

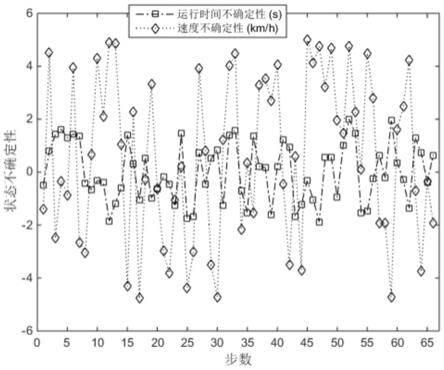
[0001]
本发明涉及轨道交通运行控制领域。更具体地，涉及一种以节能为目标的基于预测控制的高速列车节能运行曲线在线计算的方法。


背景技术：

[0002]
近些年来，随着高速铁路的快速发展，许多高速铁路系统都以高度自动化的方式运行，列车自动控制(atc)系统在高速铁路的安全和节能运营中发挥着重要作用。组成atc的关键子系统之一是列车自动运行(ato)系统，该系统主要功能是实现列车的自动驾驶，提高列车的运行效率，节省列车的运行能耗。对于ato系统来说，最重要的就是能够有效准确地跟踪列车的最佳运行速度曲线，因此，作为ato系统的参考信号，确定列车的最佳运行速度曲线无疑在列车自动运行过程中起着至关重要的作用。
[0003]
目前，大多数研究将列车速度曲线生成问题表述为最优控制问题。从最优控制的角度来看，有三种基本的数值方法可以解决列车的最优控制问题：动态规划，间接方法和直接方法。动态规划通过以递归方式将其分解为更简单的子问题，从而简化了复杂的问题。当动态规划应用于具有连续状态空间的离散系统时，通常需要通过离散化来近似。这种离散容易导致“维数诅咒”，这意味着计算成本相对于状态空间维数呈指数增长，随着维数的增大，传统的动态规划容易出现维数克死的现象。在间接方法中，一般使用变异演算来获得最优性的一阶必要条件。这些必要条件导致了哈密顿边值问题。由于最优控制问题的强烈的非线性和不稳定性，通常很难解决边值问题。与间接方法不同，所谓的直接方法通过将控制和/或状态变量(如列车牵引力、制动力，速度和位置等)的数值离散化，将原始的最优列车控制问题转换为约束数学规划问题来进行求解。近年来，一类特殊的直接方法——伪谱法，在数值最优控制领域中日益突出。从上世纪90年代开始，伪谱方法被用于解决最优控制问题，例如轨道转移，月球导航，磁控制。近年来，由于大规模计算的快速发展，伪谱法的应用范围已经逐渐扩大。然而，伪谱法在列车运行曲线计算方面应用较少。因此，本发明采用伪谱法来解决列车运行曲线计算问题。与此同时，目前大多数研究仅限于根据固定的运行参数(例如固定的列车阻力系数和静态线速度限制)对列车的参考速度曲线进行离线计算。在实际中，列车的阻力系数并不清楚，其中一些甚至随恶劣的天气条件而变化。此外，不确定的操作干扰以及临时速度限制(tsr)可能会导致意外的延误。因此，在上述情况下，如果ato仅尝试遵循离线确定的参考速度曲线，则难以确保列车的行驶性能。


技术实现要素：

[0004]
为了解决现有技术中存在的问题，本发明提出了一种基于预测控制的高速列车节能运行曲线在线计算方法，在考虑列车阻力模型不确定性和运行干扰的情况下实施列车节能运行策略，对实现高速铁路列车的节能运行和自动驾驶具有较好的参考意义和实用价值。本发明的技术方案如下：
[0005]
一种基于预测控制的高速列车节能运行曲线在线计算方法，包括如下步骤：
[0006]
s1：将线路坡度，速度限制，列车参数和列车参考速度曲线作为列车控制系统输入；
[0007]
s2：在每个采样控制周期，监测并得到列车运行的实时速度和位移信息；
[0008]
s3：根据列车的实时速度和位移信息，设计预测控制方法，在线计算列车的运行曲线，实现列车节能运行。
[0009]
步骤s3具体包括以下步骤：
[0010]
s31：将两个站点之间的轨道离散化为n个子区间，然后进一步离散为q个小区间。
[0011]
s32：设定预测控制时域，在设定的预测控制时域内，根据高速列车动力学模型、控制系统约束和控制目标，以列车的速度和位移作为状态变量，牵引力/制动力作为控制变量，形成最优节能列车控制问题。
[0012]
s33：通过取q个小区间中的每个小区间作为一个控制阶段，将s32中的最优节能列车控制问题转换成一个多阶段最优控制问题，每个控制阶段都有独立的目标函数、列车动力学模型、路径约束、边界约束和连接约束。
[0013]
s34：基于伪谱法求解多阶段最优控制问题，得出每个控制阶段的控制输出(列车运行曲线)，并将其作用于列车控制系统进行控制。
[0014]
s4：到下一个采样控制周期，重复步骤s1-s3，直到控制过程结束。
[0015]
在上述方案的基础上，步骤s31所述的将两个站点之间的轨道离散化过程具体包括如下步骤：
[0016]
s311：轨道离散化：为了解决最优列车控制问题，我们需要以适当的方式离散化两个站点之间的运行距离。首先，将两个站点之间的运行距离[s
0
,s
f
](其中s
0
,s
f
分别表示初始位置和终点位置)划分为n个子区间，以使每个子区间中的轨道坡度和速度限制保持恒定。离散点表示为s
i
,i＝0,...,n，满足s
0
＝s
0
<s
1
<...<s
n
＝s
f
。这种离散化方案通常在最优列车控制区域中采用，离散化的间隔长度取决于轨道坡度和速度限制的固定切换点。
[0017]
s312：在本发明中，我们将基于给定的样本长度l
s
将子区间进一步离散为较小的小区间，使这些小区间具有恒定的坡度和速度限制。具体来说，就是将划分好的子区间[s
i-1
,s
i
]进一步划分为区间长度相同的小区间[s
i,j-1
,s
i,j
],j＝1,...,n
i
，满足其中s
i,j
是第j个离散点，n
i
是子区间[s
i-1
,s
i
]中的小区间数量。为了确保每个小区间的长度不超过采样长度l
s
，可按照如下公式确定n
i
的值：
[0018][0019]
其中，是一个向上取整符号，表示取比自己大的最小整数。因此，在区间[s
0
,s
f
]中的小区间总数为为了进一步简化，定义其中对于所有的j＝1,...,n
i
当i＝1时k＝j，当i＝2,...,n时其中l是下标，如当l＝1时，n
1
表示第一个子区间划分的小区间数量。通过这样的转换，每个小区间都可以表示为其中k＝1,...,q。
[0020]
在上述方案的基础上，步骤s32所述的在设定预测控制时域内，根据高速列车动态运行模型、控制系统约束和控制目标，以列车的速度和位移作为状态变量，牵引力/制动力作为控制变量，形成最优控制问题。包括如下步骤：
[0021]
s321：首先，通过考虑牵引力、制动力，基本阻力和其他线阻力，将高速列车在位置s处时的纵向运动的动力学模型用以下微分方程来表示：
[0022][0023][0024]
其中，s是列车所处的位置，m为列车的质量，v(s)，t(s)分别是列车在位置s时的速度和时间，u
1
(s)，u
2
(s)分别是列车在位置s时的速度对s的导数，时间对s的导数，牵引力和制动力。r
1
(v(s))是由机械和空气摩擦引起的基本阻力，通常由以下方程表示：
[0025]
r
1
(v(s))＝a+bv(s)+cv(s)
2
ꢀꢀꢀ
(4)
[0026]
其中，a,b,c是与具体列车有关的非负系数。
[0027]
r
2
(s)由轨道坡度引起的线路阻力，进一步表示为：
[0028]
r
2
(s)＝mg sinα(s)
ꢀꢀꢀ
(5)
[0029]
其中，α(s)是在s处的轨道的倾斜角度，g是重力加速度。
[0030]
一般来说，列车严格按照计划时刻表中的时间运行，即列车必须在t
0
时刻从初始位置s
0
处以v
0
的初始速度、在t
f
时刻时以v
f
的终端速度行驶到终点位置s
f
。因此，应满足以下约束条件：
[0031]
v(s
0
)＝v
0
,t(s
0
)＝t
0
ꢀꢀꢀ
(6)
[0032]
v(s
f
)＝v
f
,t(s
f
)＝t
f
ꢀꢀꢀ
(7)
[0033]
此外，列车在运行中的速度不允许超过线路上的固定限速v
ssl
(s)和临时限速v
tsr
(s)，即：
[0034]
0<v(s)<v
max
(s)＝min{v
ssl
(s),v
tsr
(s)}
ꢀꢀꢀ
(8)
[0035]
可以看出，v
max
(s)是与位置s有关的分段函数。
[0036]
一般情况下，作用在列车上的牵引力和制动力是连续的，并受以下约束条件的约束：
[0037][0038][0039]
式中，和分别是速度v下列车的最大牵引力和最大制动力。注意到，和是非线性的函数，取决于特定的列车。
[0040]
显然，在满足上述约束的同时，列车可以有多种运行策略来完成其行程。在这些策略中，节能运行的目的是使列车在整个行程中的能量消耗达到最小。最优节能列车控制问题的控制目标可以表示为：
[0041][0042]
式中μ为列车再生制动系数。假设列车制动时的再生能量可以通过接触网立即反馈给变电站。因此，考虑再生制动方案，可降低变电站的牵引总能量消耗。上述节能列车控制问题可通过使用庞特里亚金最大值原理、伪谱法或其他直接数值方法离线解决，得到的最优列车控制和速度轨迹可作为在线列车自动控制的参考信号。
[0043]
转化后的最优节能控制问题如下所示：
[0044][0045][0046]
s322：令当前的控制步骤k对应于小区间在控制步骤k时，我们考虑在预测时域p(0<p<q)内的最优列车控制问题，此时该最优控制问题的目标函数可表示为：
[0047][0048]
最优控制问题的初始条件表示为：
[0049][0050]
其中，v
k,0
和t
k,0
分别是列车在处的实际实时速度和运行时间。在预测范围结束时，终端状态需要满足：
[0051][0052]
其中，v
k,p
和t
k,p
分别是列车在处的期望速度和运行时间。一般来说，v
k,p
和t
k,p
的值可由以下公式得到：
[0053][0054]
其中，v
refk,p
和t
refk,p
分别是列车在处由离线计算获得的参考速度和运行时间。
[0055]
最后，在预测时域p内第k个控制步骤的最优节能列车控制问题可以表述为：
[0056]
[0057][0058]
在上述方案的基础上，步骤s33所述的通过取每个子区间作为一个控制阶段，将s32中的优化控制问题转换成一个多阶段最优控制问题，具体包括如下步骤：
[0059]
将s32中的优化控制问题转换成一个多阶段最优控制问题：
[0060]
首先，定义s
0(h)
和s
f(h)
分别为控制阶段h的起始位置和终端位置，则对每个控制阶段h，都有通过考虑牵引力/制动力，基本阻力和其他线阻力，将高速列车在控制阶段h时在位置s处时沿行进的纵向运动的动力学模型建模为以下微分方程：
[0061][0062][0063]
其中v
(h)
(s)、u
1(h)
(s)、u
2(h)
(s)分别是在控制阶段h时列车在位置s时的速度对s的导数，时间对s的导数，速度，牵引力和制动力。
[0064]
转换后的多阶段最优控制问题在第k步时的目标函数为最小化在预测时域p内的列车总牵引能耗，表示为：
[0065][0066]
该多阶段最优控制问题在h控制阶段的路径约束为：
[0067]
0<v
(h)
(s)<v
max
(s)
ꢀꢀꢀ
(23)
[0068][0069][0070]
边界约束为：
[0071][0072][0073]
为使相邻的两阶段衔接起来，需满足以下连接约束：
[0074]
s
f(h)
＝s
0(h+1)
ꢀꢀꢀ
(28)
[0075]
v
(h)
(s
f(h)
)＝v
(h+1)
(s
0(h+1)
)
ꢀꢀꢀ
(29)
[0076]
t
(h)
(s
f(h)
)＝t
(h+1)
(s
0(h+1)
)
ꢀꢀꢀ
(30)
[0077]
最后，在预测范围p内第k控制步骤处的多阶段最优控制问题可以描述如下：
[0078][0079][0080]
在上述方案的基础上，步骤s34所述的基于伪谱法求解多阶段最优控制问题，得出每个控制阶段的控制输出，并将其作用于列车运行控制系统，具体包括如下步骤：
[0081]
s341：在控制步骤k时，测量获得列车的状态反馈信息：实时速度v
k,0
和运行时间t
k,0
；
[0082]
s342：使用radau伪谱法(rpm)求解预测时域p内的多阶段最优控制问题，从而得到时间最优控制序列(其中u
1*
(s),u
2*
(s)分别为最优牵引力和最优制动力)和具体过程如下：
[0083]
令状态变量x＝[v,t]
t
，控制变量u＝[u
1
,u
2
]
t
，v、t分别为列车的速度和时间，u
1
、u
2
分别为牵引力和制动力；将微分状态方程重写为如下紧凑形式：是状态变量x(s)对s的导数，在每个控制阶段h(h＝k,...k+p-1)，自变量s可表示为：
[0084][0085]
其中γ是一个新的自变量，且γ∈[-1,1]。因此，公式(20)-(21)转化为：
[0086][0087]
其中是在h控制阶段时状态变量对γ的导数，x
(h)
(γ)和u
(h)
(γ)分别是在h控制阶段时的状态变量和控制变量。
[0088]
公式(31)重构为：
[0089][0090]
路径约束为：
[0091]
0<v
(h)
(γ)<v
max
(γ)
ꢀꢀꢀ
(36)
[0092][0093][0094]
边界约束为：
[0095]
v
(k)
(-1)＝v
k,0
,t
(k)
(1)＝t
k,0
ꢀꢀꢀ
(39)
[0096]
v
(k+p-1)
(-1)＝v
k,p
,t
(k+p-1)
(1)＝t
k,p
ꢀꢀꢀ
(40)
[0097]
连接约束为：
[0098]
s
f(h)
＝s
0(h+1)
ꢀꢀꢀ
(41)
[0099]
v
(h)
(1)＝v
(h+1)
(-1)
ꢀꢀꢀ
(42)
[0100]
t
(h)
(1)＝t
(h+1)
(-1)
ꢀꢀꢀ
(43)
[0101]
此时，多阶段最优控制问题(31)-(32)转化为一个容易求解的非线性规划问题(35)-(43)，对该非线性规划问题采用现有求解器进行有效求解，如matlab中的snopt求解器，求出控制步骤k时的最优控制序列和
[0102]
s343：将计算得到的最优控制序列和生成列车运行曲线并作用于列车控制系统进行控制。
[0103]
本发明的有益技术效果如下：
[0104]
本发明考虑了基于预测控制的高速列车在线节能运行曲线计算问题，其中在列车运行过程中考虑了实时运行信息(例如状态不确定性和临时速度限制)的变化所带来的影响，并以节能为目标，根据预测控制方法对该问题进行了建模。在每个控制步骤，最优控制问题转化为多阶段最优控制问题然后通过伪谱法高效求解。通过在每个步骤中反复解决预测时域内的列车最优控制问题，可以在线获取列车整个行程的节能列车速度曲线，这种方法具有计算效率高和鲁棒性好等优点，可实现对高速列车运行速度曲线的实时计算。
附图说明
[0105]
本发明有如下附图：
[0106]
图1中，a图为：本发明提供的离线计算的列车速度轨迹，b图为：离线计算的列车控制轨迹。
[0107]
图2中，a图为：使用本发明所提出的方法在线计算的列车速度轨迹，b图为：在线计算的列车控制轨迹。
[0108]
图3中，a图为：本发明提供的使用cp方法在线计算的列车速度轨迹，b图为：使用cp方法在线计算的列车控制轨迹。
[0109]
图4示出本发明提供的所有步骤的列车运行时间和速度不确定性示意图。
[0110]
图5中，a图为：本发明提供的考虑不确定性状态下的列车速度轨迹，b图为：本发明提供的考虑不确定性状态下的列车控制轨迹。
[0111]
图6中，a图为：本发明提供的有无tsr的列车最佳速度对比，b图为：有无tsr的列车最佳控制对比。
[0112]
图7中，a图为：本发明提供的具有不同tsr的6个场景的列车速度，b图为：本发明提供的具有不同tsr的6个场景的列车运行时间。
具体实施方式
[0113]
为了更清楚地说明本发明，下面结合优选实例和附图对本发明做进一步的说明。本领域技术人员应当理解，下面所具体描述的内容是说明性的而非限制性的，不应以此限制本发明的保护范围。
[0114]
本发明中的所有实例均使用北京到天津的高铁线路数据和crh3列车的参数。北京南站和天津站之间的距离是122.12公里。线路的静态速度限制和轨道坡度如图1所示，crh3高速列车的参数如表1所示。
[0115]
表1 crh3高速列车的参数
[0116][0117]
最大牵引力和制动力(均以kn表示)为
[0118][0119][0120]
列车的参考速度轨迹以及根据上述线路和列车数据离线计算出的相应控制如图1所示。
[0121]
crh3型号的列车在北京南站和天津站之间的运行时间为t
f
＝1800s，所考虑的铁路线路离散化的样本长度选择为l
s
＝2km，将整段线路离散化q＝66个小区间。因此，共有q个多阶段最优控制问题需要依次求解。对于前q-p+1个最优控制问题，预测时域设置为p＝6。而在后p-1个最优控制问题中，在控制步骤k(k＝q-p+2,...,q)时，预测时域设为q-k+1。此外，在每一步中，只有第一组最优控制序列被应用到列车的控制上。
[0122]
若不考虑不确定性因素的影响，列车速度和控制轨迹如图2所示。从图中可以看出，用本发明的上述方法在线获得的速度剖面与离线计算的速度剖面几乎没有差别。然而，图2中的控制轨迹显示出在巡航阶段(从大约30到80公里)比离线轨迹稍微多一些波动。由于轨道离散化方案的不同，在线获得的控制比离线控制的波动更大。在控制力可以在线施加到列车系统之前，需要消除或消除这些波动。在线和离线计算的列车速度曲线的牵引能耗分别为1.0621
×
107kj和1.0530
×
107kj，偏差仅为0.86％。另外，整个行程的速度曲线离线计算时间约为28秒，而采用我们的在线生成速度曲线的方法，每一步的平均计算时间仅为0.5秒左右。
[0123]
为了证明伪谱法(pm)在解决在线列车控制问题时的节能性能，我们在每个步骤中
都使用控制参数化(cp)方法重新计算上述示例。图3描绘了使用cp方法在线获得的列车速度和控制轨迹。采用cp法计算列车牵引能耗为1.0880
×
107kj，比pm法提高2.4％，平均每步计算时间约为0.8s。
[0124]
我们进一步考虑由列车阻力系数变化引起的系统模型不确定性，给定每一步扰动列车速度和终点运行时间的界值分别为v
b
＝5km/h，t
b
＝2s。图4绘制了所有步骤的列车速度和运行时间不确定扰动。考虑不确定性因素影响的在线计算列车速度和控制曲线如图5所示。考虑图4中所示的不确定性状态时，列车牵引能量消耗为1.0550
×
107kj，全程实际运行时间为1797.6秒。这种总运行时间偏差是由每一步列车速度和运行时间的不确定所造成的。在本例中，延迟时间的阈值设置为t
d
＝10s。step 6中的延迟恢复过程在计算过程中没有触发，即使每个步骤都存在状态不确定性。每一步的平均计算时间约为0.6秒。
[0125]
综上所述，上述离线和在线列车控制问题的计算结果见表2。由于样本长度为l
s
＝2km，最高速度为350km/h的列车在l
s
上的最小运行时间约为20秒，远大于每个控制步骤的平均计算时间。此外，预测距离最大为l
s
×
p＝12km，这对于列车从最高速度350km/h以紧急制动减速度制动到停车都是足够的。这些都表明本发明的基于mpc的高速列车实时速度曲线生成方案可以实现。
[0126]
表2离线和在线列车最优控制问题的仿真结果
[0127][0128]
为了证明本发明所提出的方法在处理操作干扰方面的性能，我们考虑了旅途中临时速度限制(tsr)的情况。250km/h的tsr发生在[43.890，48.269]km区间处，当列车接近该间隔时，它将收到此tsr信息。该速度限制低于线路的静态速度限制，因此，对于该间隔和剩余行程，离线获得的参考速度曲线将是不可行的。通过使用本发明提出的算法，a to可以在线调整驾驶策略以适应tsr。
[0129]
在这种场景下，样本长度同样将设为l
s
＝2km，并且延迟时间的阈值设置为t
d
＝10s。在图6中绘制了考虑到该tsr的计算出的列车速度和控制轨迹以及离线获得的轨迹。在这种情况下，本发明所提出的方法在step 6中，由tsr引起的延迟时间大于t
d
＝10s，延迟恢复过程是在大约52.2km(在tsr区间之后)触发的。因此，列车剩余行程的参考速度曲线将根据当前列车状态重新进行计算。在这个过程中，根据新的参考信号，ato系统将反复在线计算速度曲线，直到列车到达终点站为止。
[0130]
在此实例中，列车在tsr区间消耗的牵引能量为1.0710
×
10
7
kj，比离线策略大1.7％。这是由于tsr的存在，列车在tsr间隔之后必须应用更长的全牵引策略才能准时到达终点站。此外，整个行程的实际旅行时间为1802.9秒。
[0131]
为证明本发明所提出方法对不同干扰延误的鲁棒性，接下来针对不同的干扰延误场景进行分析。我们考虑在不同位置具有不同干扰延误时间的6种场景。这些场景的列车速度曲线都是通过使用本发明所提出的方法进行在线计算的。图7绘制了6种场景下的运行速度和时间曲线，图7中a图为速度轨迹示意图，b图为时间曲线示意图。由于6种场景的运行时间差别不大，在图7b中6种场景的轨迹呈现出重叠的状态。表3的前两列列出了不同场景下发生延迟的具体时间和位置。从图7和表3可以看出，对于6种不同场景，不同位置的延迟时间几乎相同，并且由此产生的速度轨迹也差别不大。此外，全行程的计算能耗和6种场景下每个控制步骤的平均计算时间见表3的最后两列，能耗和计算时间的平均方差分别为1.1513
×
105kj和0.15s，这意味着对于6种不同场景，能量消耗和计算时间之间只有很小的偏差。这些特征说明了我们提出的基于预测控制的高速列车在线曲线计算方法对不同的列车干扰延误具有鲁棒性。
[0132]
表3 6种场景下的干扰延误时间，位置，能耗和平均计算时间
[0133][0134]
显然，本发明的上述实施例仅仅是为清楚地说明本发明所做的举例，而并非是对本发明的实施方式的限定，对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动，这里无法对所有的实施方式予以穷举，凡是属于本发明的技术方案所引申出的显而易见的变化或变动仍处于本发明的保护范围之列。
[0135]
本说明书中未做详细描述的内容属于本领域专业技术人员公知的现有技术。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除