电动汽车充电策略的确定方法及装置与流程

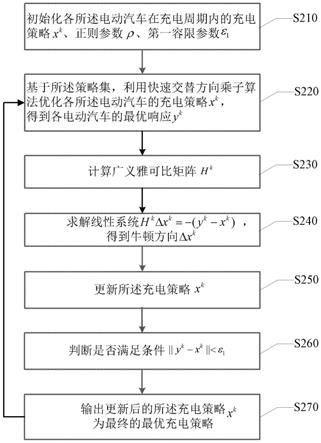
[0001]
本公开涉及电动汽车有序充放电控制技术领域，尤其涉及一种电动汽车充电策略的确定方法及装置。


背景技术：

[0002]
电动汽车v2g(vehicle to grid)技术是指电动汽车给电网送电的技术，其核心思想在于：利用大量电动汽车的储能源作为电网和可再生能源的缓冲，实现电动汽车和电网的双向互动。具体来说，当电网负荷过高时，电动汽车会给电网送电；而当电网负荷低时，电网可以将多余的发电量存储在电动汽车中，避免造成资源的浪费。通过这种v2g技术，电动汽车车主可以在低电价时从电网购电存储在其电池中，高电价时向电网售电，从而获得一定的收益，同时，可以大大缓解电网效率低以及可再生能源波动的问题。
[0003]
传统的充电站和插入式电动汽车之间的交互机制要求每一个电动汽车和嵌入在充电站中的聚合器进行通信。具体来说，每一个电动汽车通过增加/减少其充电请求或者将其充电请求从高价时段转移到低价时段，从而对由聚合器决定的动态电价分别进行响应。然而，由于电动汽车之间的相互独立性，这种传统的交互机制并不一定能够找到使充电站能源成本最小化的最优充电策略组合，当问题规模很大时，还会增加系统的计算和通信负担。此外，在已有的电动汽车充电研究工作中，大多只考虑了车载电池在充电站中仅有充电和闲置两个状态，只能通过聚合器直接进行控制。


技术实现要素：

[0004]
鉴于上述问题，本发明提供了一种电动汽车充电策略的确定方法及装置，以至少解决部分上述问题。
[0005]
本公开一方面提供了一种电动汽车充电策略的确定方法，包括：利用非合作博弈框架对电动汽车的充电问题建模，该非合作博弈模型包括充电站中的电动汽车集合、所述电动汽车集合中各电动汽车的策略集和各所述电动汽车的充电成本，其中，各所述电动汽车的策略集和充电成本均依赖其自身及所述电动汽车集合中其它电动汽车的充电策略；基于牛顿不动点法的分布式纳什均衡搜索算法求解所述非合作博弈模型，获得各所述电动汽车的最优充电策略，在满足所述各电动汽车充电需求及充电站约束条件的同时，以使所述充电站的总能源成本最小。
[0006]
可选地，所述非合作博弈模型包括：令g表示所述非合作博弈模型，n表示所述电动汽车集合，n＝{1，2，...，n}，χ
n
表示各所述电动汽车n∈n的策略集，f
n
表示各所述电动汽车n的充电成本函数，则：
[0007]
g＝{n，{χ
n
}
n∈n
，{f
n
}
n∈n
}；
[0008]
令表示所述非合作博弈模型的纳什均衡解，其中，χ表示所有电动汽车的联合策略集，表示所述电动汽车n在纳什均衡解下的最优充电策略，表示所述电动汽车集合中除所述电动汽车n以外的其它电动汽车在纳什均衡解下的最优充电策
x
k
)，得到牛顿方向δx
k
；s250，更新所述充电策略x
k
，x
k+1
＝x
k
+δx
k
；s260，判断是否满足条件||y
k-x
k
||＜ε
1
；s270，如果条件不满足，继续执行步骤s220，否则，跳出循环，输出更新后的所述充电策略x
k
为最终的最优充电策略。
[0020]
可选地，所述基于所述策略集，利用快速交替方向乘子算法优化各所述电动汽车的充电策略x
k
，得到各所述电动汽车的最优响应y
k
包括：s221，初始化对偶变量、拉格朗日乘子向量、第二容限参数ε
2
、增广拉格朗日乘子(、当前给定充电策略x
k
，r
tn
表示实数集上维数为tn的列向量；s222，基于当前的对偶变量、拉格朗日乘子向量、正则参数、增广拉格朗日乘子、当前给定充电策略，在所述策略集的约束下，根据更新各所述电动汽车的最优响应y，其中，表示增广拉格朗日函数，s
1
表示所述策略集中约束条件(2)、(3)、(4)组成的集合；s223，更新当前对偶变量z
v
，，其中，z表示当前求解的对偶变量z
v
，s
2
表示所述策略集中约束条件(1)构成的集合；s224，更新当前拉格朗日乘子向量λ
v
，s225，校正当前对偶变量、拉格朗日乘子向量；s226，判断是否满足条件|λ
v-λ
v-1
||≤ε
2
，如果条件满足，将y
v
作为最优响应y
k
输出，否则继续执行步骤s222。
[0021]
可选地，所述增广拉格朗日函数包括：
[0022][0023]
其中，i
1
(y)和为两个示性函数，如果y∈s
1
，则i
1
(y)＝1，否则i
1
(y)＝0；如果，则，否则
[0024]
可选地，所述校正当前对偶变量、拉格朗日乘子向量包括：所述快速交替方向乘子算法初始化时，初始化中间变量η
v
；更新中间变量η
v
，并根据更新得到的η
v+1
校正当前对偶变量、拉格朗日乘子向量，包括：
[0025][0026][0027][0028]
本公开另一方面提供了一种电动汽车充电策略的确定装置，包括：建模模块，用于利用非合作博弈框架对电动汽车的充电问题建模，非合作博弈模型包括充电站中的电动汽车集合、所述电动汽车集合中各电动汽车的策略集和各所述电动汽车的充电成本，其中，各所述电动汽车的策略集和充电成本均依赖其自身及所述电动汽车集合中其它电动汽车的充电策略；优化模块，用于基于牛顿不动点法的分布式纳什均衡搜索算法求解所述非合作博弈模型，获得各所述电动汽车的最优充电策略，从而在满足各电动汽车充电需求及充电站约束条件的同时，使所述充电站的总能源成本最小。
[0029]
在本公开实施例采用的上述至少一个技术方案能够达到以下有益效果：
[0030]
本公开提供的方法除了考虑了电动汽车的车载电池在充电站中存在充电和闲置两种状态，还考虑了车载电池的放电状态，所有电动汽车并不直接受聚合器的控制，而是相互之间进行策略交互，在此策略机制下，利用非合作博弈框架对电动汽车的充电问题进行建模，使充电站中的每个电动汽车均根据充电站中的所有电动汽车的策略选择自己的最优策略，从而极小化自己的充电支付成本。本公开证实了该非合作博弈存在唯一的纳什均衡(nash equilibrium)解且恰好对应于充电站能源成本极小化问题的最优解。此外，本公开提出了一种基于牛顿不动点法(newton fixed-point method)的分布式算法求解非合作博弈的纳什均衡点。在此过程中，利用快速交替方向乘子法(fast alternating direction multiplier method(fast-admm))以确定电动汽车的最优响应。本公开提供的方法考虑了充电站中多个电动汽车的策略交互关系，充分利用了电动汽车充放电的灵活性，能够在满足电动汽车充电需求及充电站约束条件的同时，使充电站的总能源成本最小。
附图说明
[0031]
为了更完整地理解本公开及其优势，现在将参考结合附图的以下描述，其中：
[0032]
图1示意性示出了本公开实施例提供的一种电动汽车充电策略的确定方法的应用场景；
[0033]
图2示意性示出了本公开实施例提供的一种充电站和电动汽车交互机制示意图；
[0034]
图3示意性示出了本公开实施例提供的一种基于牛顿不动点法的分布式纳什均衡搜索算法的流程图。
具体实施方式
[0035]
以下，将参照附图来描述本公开的实施例。但是应该理解，这些描述只是示例性的，而并非要限制本公开的范围。在下面的详细描述中，为便于解释，阐述了许多具体的细节以提供对本公开实施例的全面理解。然而，明显地，一个或多个实施例在没有这些具体细节的情况下也可以被实施。此外，在以下说明中，省略了对公知结构和技术的描述，以避免不必要地混淆本公开的概念。
[0036]
在此使用的术语仅仅是为了描述具体实施例，而并非意在限制本公开。在此使用的术语“包括”、“包含”等表明了所述特征、步骤、操作和/或部件的存在，但是并不排除存在或添加一个或多个其他特征、步骤、操作或部件。
[0037]
在此使用的所有术语(包括技术和科学术语)具有本领域技术人员通常所理解的含义，除非另外定义。应注意，这里使用的术语应解释为具有与本说明书的上下文相一致的含义，而不应以理想化或过于刻板的方式来解释。
[0038]
附图中示出了一些方框图和/或流程图。应理解，方框图和/或流程图中的一些方框或其组合可以由计算机程序指令来实现。这些计算机程序指令可以提供给通用计算机、专用计算机或其他可编程数据处理装置的处理器，从而这些指令在由该处理器执行时可以创建用于实现这些方框图和/或流程图中所说明的功能/操作的装置。
[0039]
因此，本公开的技术可以硬件和/或软件(包括固件、微代码等)的形式来实现。另外，本公开的技术可以采取存储有指令的计算机可读介质上的计算机程序产品的形式，该
计算机程序产品可供指令执行系统使用或者结合指令执行系统使用。在本公开的上下文中，计算机可读介质可以是能够包含、存储、传送、传播或传输指令的任意介质。例如，计算机可读介质可以包括但不限于电、磁、光、电磁、红外或半导体系统、装置、器件或传播介质。计算机可读介质的具体示例包括：磁存储装置，如磁带或硬盘(hdd)；光存储装置，如光盘(cd-rom)；存储器，如随机存取存储器(ram)或闪存；和/或有线/无线通信链路。
[0040]
如图1、图2所示，充电站通过聚合器设置合适的电价来协调有限集合n＝{1，2，...，n}的电动汽车在充电周期t＝{1，2，..，t}上的充电行为。
[0041]
本公开提供了一种电动汽车充电策略的确定方法，包括步骤s100～s200。
[0042]
s100，利用非合作博弈框架对电动汽车的充电问题建模，该非合作博弈模型包括充电站中的电动汽车集合、电动汽车集合中各电动汽车的策略集和各电动汽车的充电成本，其中，各电动汽车的策略集和充电成本均依赖其自身及电动汽车集合中其它电动汽车的充电策略。
[0043]
s200，基于牛顿不动点法的分布式纳什均衡搜索算法求解非合作博弈模型，获得各电动汽车的最优充电策略，在满足各电动汽车充电需求及充电站约束条件的同时，使充电站的总能源成本最小。
[0044]
具体的，在本公开实施例中，最小化充电站的总能源成本的问题可描述为：
[0045][0046]
其中，c
tol
表示充电站的总能源成本，c
t
(l
t
)表示充电站在t时刻向上级供电设施购买l
t
单位的能源所支付的费用，α
t
、β
t
表示与能源成本有关的两个正参数，χ表示所有电动汽车的联合策略集。
[0047]
定义x
n
＝(x
n，1
，x
n，2
，..，x
n，t
)
t
为电动汽车n在整个充电周期内的充电策略，充电策略x
n，t
为正值时，表示电动汽车n在t时刻的充电策略为充电，x
n，t
为负值时，表示电动汽车n在t时刻的充电策略为放电，x
n，t
为零时，表示电动汽车n在t时刻的充电策略为闲置，x
n，t
的数值表示电动汽车n在t时刻的充放电功率。
[0048]
策略集包括了各电动汽车的充电策略的约束条件，包括：
[0049][0050]
其中，r
n
表示电动汽车n在整个充电周期内所需的能源，x
n，t
表示电动汽车n在t时刻的充电策略，分别表示电动汽车n的初始、最小以及最大的电池容量，表示电动汽车n的额定充电功率，l
max
表示充电站的最大可允许负载。
[0051]
令f
n
(x
n
，x-n
)表示电动汽车n∈n的充电成本函数，x
n
表示各所述电动汽车n在充电周期t＝{1，2，...，t}内各时间点的充电策略构成的列向量，定义为x
n
＝(x
n，1
，x
n，2
，...，
x
n，t
)
t
，其中，x
n，t
表示所述电动汽车n在t∈{1，2，...，t}时刻的充电策略，x-n
表示所述电动汽车集合中除所述电动汽车n以外的其它电动汽车的充电策略，该变量同时表明电动汽车n的充电成本也受所述电动汽车集合中其他所述电动汽车的充电策略的影响，则：
[0052][0053]
其中，γ
n
表示所述电动汽车n的能源消耗对充电站收益的贡献值，α
t
、β
t
分别表示与充电成本有关的两个正参数，δ表示获利指标，c
t
(l
t
)表示充电站在t时刻向上级供电设施购买l
t
单位的能源所支付的费用，
[0054][0055][0056]
基于充电站中的电动汽车集合、上述电动汽车集合中各电动汽车的策略集和各电动汽车的充电成本的计算函数，令g表示所述非合作博弈模型，n表示所述电动汽车集合，n＝{1，2，...，n}，χ
n
表示各所述电动汽车n∈n的策略集，f
n
表示各所述电动汽车n的充电成本函数，则：
[0057]
g＝{n，{χ
n
}
n∈n
，{f
n
}
n∈n
}。
[0058]
一般而言，在博弈论中，用纳什均衡来描述非合作博弈的解，该纳什均衡解刻画了玩家如何参与博弈。在本公开实施例中，令表示所构建非合作博弈的纳什均衡解，其中，χ表示所有电动汽车的联合策略集，表示电动汽车n在纳什均衡解下的最优充电策略，表示除电动汽车n以外，其他所有电动汽车在纳什均衡解下的最优充电策略，则：
[0059][0060]
在此约束下，没有任何一个电动汽车可以单方面偏离纳什均衡策略以降低自己的支付成本。
[0061]
参阅图3，在本公开实施例中，步骤s220包括s210～s270，具体实施过程如下。
[0062]
s210，初始化各电动汽车在充电周期内的充电策略x
k
、正则参数ρ、第一容限参数ε
1
。
[0063]
s220，基于策略集，利用快速交替方向乘子算法优化各电动汽车的充电策略x
k
，得到各电动汽车的最优响应y
k
，即在其他所有电动汽车不改变充电策略的情况下，每个电动汽车的最优充电策略的组合。
[0064]
s230，通过，计算广义雅可比矩阵h
k
。
[0065]
s240，求解线性系统h
k
δx
k
＝-(y
k-x
k
)，得到牛顿方向δx
k
。
[0066]
s250，更新充电策略x
k
，x
k+1
＝x
k
+δx
k
。
[0067]
s260，判断是否满足条件||y
k-x
k
||＜ε
1
。
[0068]
s270，如果条件不满足，继续执行步骤s2，否则，跳出循环，输出更新后的充电策略
x
k
。
[0069]
本公开提供的方法证实了该非合作博弈存在唯一的纳什均衡解且恰好对应于充电站能源成本极小化问题的最优解，并利用本公开提出了一种基于牛顿不动点法的分布式算法求解非合作博弈的纳什均衡点，在此过程中，利用快速交替方向乘子法以确定电动汽车的最优响应，该方法具有更快的收敛速度。
[0070]
步骤s220包括s221～s220。
[0071]
s221，初始化对偶变量、拉格朗日乘子向量、第二容限参数ε
2
、增广拉格朗日乘子当前给定充电策略x
k
，r
tn
表示实数集上维数为tn的列向量。
[0072]
s222，基于当前的对偶变量、拉格朗日乘子向量、正则参数、增广拉格朗日乘子、当前给定充电策略，在所述策略集的约束下，根据更新各所述电动汽车的最优响应y，其中，表示增广拉格朗日函数，s
1
表示所述策略集中约束条件(2)、(3)、(4)组成的集合。
[0073]
s223，更新当前对偶变量z
v
，，其中，z表示当前求解的对偶变量z
v
，s
2
表示所述策略集中约束条件(1)构成的集合。
[0074]
s224，更新当前拉格朗日乘子向量λ
v
，
[0075]
s225，校正当前对偶变量、拉格朗日乘子向量。
[0076]
快速交替方向乘子算法初始化时，初始化中间变量η
v
，用于在快速交替方向乘子算法迭代中校正对偶变量、拉格朗日乘子向量。
[0077]
更新中间变量η
v
，并根据更新得到的η
v+1
校正当前对偶变量、拉格朗日乘子向量，包括：
[0078][0079][0080][0081]
s226，判断是否满足条件||λ
v-λ
v-1
||≤ε
2
，如果条件满足，将y
v
作为最优响应y
k
输出，否则继续执行步骤s222以更新当前最优响应y
v
。
[0082]
在本公开实施例中，利用快速交替方向乘子法求解电动汽车最优充电策略的收敛速度较快，可以理解的，还可以选用其他局部搜索算法进行最优充电策略搜索。
[0083]
本公开提供的一种电动汽车充电策略的确定方法，除了考虑了电动汽车的车载电池在充电站中存在充电和闲置两种状态，还考虑了车载电池的放电状态，所有电动汽车并不直接受聚合器的控制，而是相互之间进行策略交互，在此策略机制下，利用非合作博弈框架对电动汽车的充电问题进行建模，使充电站中的每个电动汽车均根据充电站中的所有电动汽车的策略选择自己的最优策略，从而极小化自己的充电支付成本。本公开证实了该非合作博弈存在唯一的纳什均衡解且恰好对应于充电站能源成本极小化问题的最优解，提出了一种基于牛顿不动点法的分布式算法求解非合作博弈的纳什均衡点，在此过程中，利用快速交替方向乘子法以确定电动汽车的最优响应。本公开提供的方法考虑了充电站中多个
电动汽车的策略交互关系，充分利用了电动汽车充放电的灵活性，能够在满足电动汽车充电需求及充电站约束条件的同时，使充电站的总能源成本最小。
[0084]
本公开另一方面提供了一种电动汽车充电策略的确定装置，包括：建模模块，优化模块。
[0085]
建模模块，用于利用非合作博弈框架对电动汽车的充电问题建模，该非合作博弈模型包括充电站中的电动汽车集合、电动汽车集合中各电动汽车的策略集和各电动汽车的充电成本，其中，各电动汽车的策略集和充电成本均依赖其自身及电动汽车集合中其它电动汽车的充电策略。
[0086]
优化模块，用于基于牛顿不动点法的分布式纳什均衡搜索算法求解该非合作模型，获得各电动汽车的最优充电策略，从而在满足各电动汽车充电需求及充电站约束条件的同时，使充电站的总能源成本最小。
[0087]
具体的，本公开提供的一种电动汽车充电策略的确定装置具有与上述电动汽车充电策略的确定方法的技术特征相同，且具有相同的有益效果，在此不做赘述。
[0088]
可以理解的是，建模模块、优化模块可以合并在一个模块中实现，或者其中的任意一个模块可以被拆分成多个模块。或者，这些模块中的一个或多个模块的至少部分功能可以与其他模块的至少部分功能相结合，并在一个模块中实现。根据本发明的实施例，建模模块、优化模块中的至少一个可以至少被部分地实现为硬件电路，例如现场可编程门阵列(fpga)、可编程逻辑阵列(pla)、片上系统、基板上的系统、封装上的系统、专用集成电路(asic)，或可以以对电路进行集成或封装的任何其他的合理方式等硬件或固件来实现，或以软件、硬件以及固件三种实现方式的适当组合来实现。或者，建模模块、优化模块中的至少一个可以至少被部分地实现为计算机程序模块，当该程序被计算机运行时，可以执行相应模块的功能。
[0089]
本领域技术人员可以理解，本公开的各个实施例和/或权利要求中记载的特征可以进行多种组合或/或结合，即使这样的组合或结合没有明确记载于本公开中。特别地，在不脱离本公开精神和教导的情况下，本公开的各个实施例和/或权利要求中记载的特征可以进行多种组合和/或结合。所有这些组合和/或结合均落入本公开的范围。
[0090]
尽管已经参照本公开的特定示例性实施例示出并描述了本公开，但是本领域技术人员应该理解，在不背离所附权利要求及其等同物限定的本公开的精神和范围的情况下，可以对本公开进行形式和细节上的多种改变。因此，本公开的范围不应该限于上述实施例，而是应该不仅由所附权利要求来进行确定，还由所附权利要求的等同物来进行限定。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除