一种基于朴素贝叶斯模型的乐器种类识别方法和系统与流程

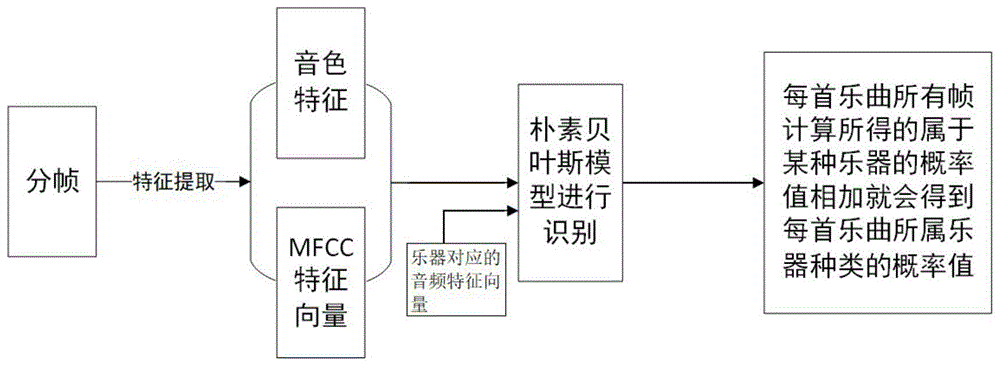
本发明是关于一种基于朴素贝叶斯模型的乐器种类识别方法和系统，属于乐器识别技术领域。

背景技术：

近年来，随着互联网时代的快速发展，音乐的应用越来越多的影响着人们的日常生活，数字音乐在娱乐领域也呈现爆炸式的增长，人们的生活中并不缺少音乐，音乐社区逐渐普及、p2p的传播方式也逐渐盛行开来，如何帮助人们找到自己需要的音乐则是音乐识别技术未来发展的重要方向。随着音乐识别技术的发展，从歌名、歌手等文本方面进行音乐识别已经广泛普及，到了九十年代发展到基于旋律和节奏等乐理特征的识别，这种基于乐理特征的识别技术出现后就直接成为了应用极为广泛的技术，并且推动了音乐识别技术的发展。1980-1996年，基于音乐识别的专利申请开始起步，但总量不多，从1998年开始至2008年，音乐识别技术的专利数量开始增加，也是音乐识别技术的快速发展阶段，其中包括基于文本属性、旋律节奏属性的情感识别和音乐风格识别。

目前，对乐曲中使用的乐器进行识别的系统还不多见。这是因为，对于数据集规模比较大的曲库，相较于文本属性特征或是旋律节奏识别，识别乐曲所使用的乐器存在较大难度，虽然某些乐器之间，从波形图来分析具有很大的区别度，但仅单独从音调、尖声和响度等特征，对乐曲中乐器进行识别是远远不够的，因此有必要对更精准，更具有表征性的音频特征分析，才能实现区别不同乐器弹奏的不同声音。音色是声音质量的属性，而非声音的响度和强度，能区分不同乐器演奏同一乐符在听觉上的不同。例如，人的听觉系统可以区分出4410hz的小提琴和双簧管，原因在于它们的高频泛音成分不相同，高频成分的幅度也不相同，而这种不同就是音色。故区分乐曲中不同乐器的关键点就是对乐器的音色进行区分，但如何以特征值的方式对乐曲进行表征是本领域亟待解决的问题。

技术实现要素：

针对上述现有技术的不足，本发明的目的是提供了一种基于朴素贝叶斯模型的乐器种类识别方法和系统，其通过这种数据化的音乐特征提取的方式，实现人工智能对乐器的种类、音色、技法的识别，帮助精细化区分其同质化和异质化乐器之间的关系，尤其是同质性乐器种类的音响细分、音色相似度、技术重合度的人工分离和精准辨别。

为实现上述目的，本发明提供了一种基于朴素贝叶斯模型的乐器种类识别方法，包括以下步骤：s1将待识别的乐曲分为若干音频帧；s2提取音频帧中的时域信息、频域信息与倒频域信息以及梅尔频率倒谱系数，形成与音频帧对应的特征向量；s3将已有的若干个乐器对应的音频特征向量和所有的音频帧对应的特征向量输入至朴素贝叶斯模型，根据乐器出现在乐曲中的概率对乐器进行识别。

进一步，若乐器出现在乐曲中的概率超过阈值，则判断乐器出现在乐曲中，若乐器出现在乐曲中的概率未超过阈值，则判断乐器没有出现在乐曲中。

进一步，乐曲中使用的乐器包括主要乐器和次要乐器，通过朴素贝叶斯方法模型获得各乐器出现在乐曲中的概率区分主要乐器和次要乐器。

进一步，出现在乐曲中的概率最高的乐器为主要乐器，其他出现在乐曲中的乐器为次要乐器。

进一步，朴素贝叶斯模型的输出公式为：

其中，xi代表一首乐曲x的某一帧，一共有z帧；yj代表某一种乐器，一共有n种乐器。

进一步，s3的具体操作过程为：s3.1将若干个乐器对应的音频特征向量和音频帧对应的特征向量输入至经过预训练的朴素贝叶斯模型；s3.2采用朴素贝叶斯模型的输出公式计算p(y1|xi),p(y2|xi),…,p(yn|xi)；s3.3通过公式得到乐器yj出现在乐曲x中的概率。

进一步，经过预训练的朴素贝叶斯模型的预训练过程为：向原始朴素贝叶斯模型输入演奏乐器类型已知的乐曲，乐曲根据朴素贝叶斯模型的输出公式获得某一乐器出现在乐曲中的概率，判断概率是否超过阈值，将判断结果与实际演奏乐曲的类型进行比较，若结果相同，则输入朴素贝叶斯模型为最终输出模型；若结果不相同，则调整朴素贝叶斯模型的输出公式，直至结果相同为止。

进一步，频域信息通过将对每一音频帧做傅里叶变换获得，倒频域信息通过将频域信息构成的频域图进行旋转，并用灰度图表示频域图的幅度获得；时域信息通过将频域图按照时间维度堆叠获得。

进一步，对若干音频帧加上汉明hanmming窗以防止频率泄漏。

本发明还公开了一种基于朴素贝叶斯模型的乐器种类识别系统，包括：预处理模块，用于将待识别的乐曲分为若干音频帧；特征提取模块，用于提取音频帧中的时域信息、频域信息与倒频域信息以及梅尔频率倒谱系数，形成与音频帧对应的特征向量；识别模块，用于将若干个乐器对应的音频特征向量和所有的音频帧对应的特征向量输入至朴素贝叶斯模型，根据乐器出现在乐曲中的概率对乐器进行识别。

本发明由于采取以上技术方案，其具有以下优点：

1、本发明通过这种数据化的音乐特征提取的方式，实现人工智能对乐器的种类、音色、技法的识别，帮助精细化区分其同质化和异质化乐器之间的关系，尤其是同质性乐器种类的音响细分、音色相似度、技术重合度的人工分离和精准辨别。

2、本发明中对音乐特征的提取、提取的特征相量的方式，可以减少乐曲中乐器识别的时间消耗，且不会影响乐器识别的精度和准确性。

3、本发明中方法能够广泛地应用在音乐欣赏、音乐分类和音乐推荐等多个领域，由于乐曲中使用的乐器在很大程度上影响着乐曲的风格，因此本发明在音乐信息检索中也会发挥一定作用。

4、本发明采用朴素贝叶斯分类模型对乐曲进行训练，采用概率的方式表征乐曲中可能对应的乐器，使人工智能模型学习可以应用于音乐中的关键元素以及常见的音乐结构与规则识别，为人工智能更好的应用于音乐领域，如修音、作曲等方面提供了参考和借鉴。

附图说明

图1是本发明一实施例中基于朴素贝叶斯模型的乐器种类识别方法的流程图；

图2是本发明一实施例中对于乐曲进行预处理过程的流程图；

图3是本发明一实施例中音频帧音色特征提取过程的流程图；

图4是本发明一实施例中音频帧梅尔倒谱系数特征特征提取过程的流程图；

图5是本发明一实施例中朴素贝叶斯分类模型识别过程的流程图；

图6是本发明一实施例中朴素贝叶斯分类模型训练过程的流程图。

具体实施方式

为了使本领域技术人员更好的理解本发明的技术方向，通过具体实施例对本发明进行详细的描绘。然而应当理解，具体实施方式的提供仅为了更好地理解本发明，它们不应该理解成对本发明的限制。在本发明的描述中，需要理解的是，所用到的术语仅仅是用于描述的目的，而不能理解为指示或暗示相对重要性。

本发明是通过提取乐曲的音色特征和梅尔倒谱系数(mfcc)特征融合形成乐曲的特征向量，将特征向量作为输入，使用朴素贝叶斯模型识别演奏乐曲的乐器，演奏乐曲的乐器包括起主导作用的主要乐器以及和主导乐器配合的几种次要乐器，例如一首乐曲是钢琴主旋律，即钢琴为主要乐器，该乐曲还包括小提琴、长笛等乐曲的伴奏，即小提琴、长笛等乐曲为次要乐器。本发明中的技术方案还可以用于区分次要乐器中各乐器的重要程度。

实施例一

一种基于朴素贝叶斯模型的乐器种类识别方法，如图1所示，包括以下步骤：

s1将待识别的乐曲分为若干音频帧，确定音频帧的帧数。如图2所示，将原始数据集中的每首乐曲都划分为多个音频帧。紧接着对音频帧加上汉明hanmming窗以防止频率泄漏，作用是为了使帧和帧之间变得平滑，消除吉布斯效应。为了既保存时域信息同时也保存频域信息，需要对经过分帧和加窗后的音频帧进行短时傅里叶变换，以获得声谱图。

短时傅里叶变换生成声谱图的过程为：

对乐曲的长信号进行分帧，加窗口；对每一帧音频帧做傅里叶变换；此时的音频帧为短时信号，即为短时傅里叶变换。将频谱图旋转；将频谱图幅度用灰度图来表示；将傅里叶变换获得的频域图按照时间维度堆叠最后就会得到声谱图。频域信息通过将对每一音频帧做傅里叶变换获得，倒频域信息通过将频域信息构成的频域图进行旋转，并用灰度图表示频域图的幅度获得；时域信息通过将频域图按照时间维度堆叠获得。

s2提取音频帧中的时域信息、频域信息与倒频域信息以及梅尔频率倒谱系数，形成与音频帧对应的特征向量。

如图3所示，基于mpeg-7(multimediacontentdescriptioninterface)标准，从时域(音色的时间域)、频域(音色波形的频率)与倒频域(反向的音色波形频率)三个层面对乐器音色进行特征性捕捉，对原始数据集中每首乐曲的每一帧这三个层面的音色特征元素进行精细提取与存储。

如图4所示，提取梅尔频率倒谱系数(melfrequencycepstrumcoefficient,mfcc)的过程为：

2.1预加重

如果数据在低频的强度大于高频，就会不利于处理，因此需要滤去数据中的低频成分，使高频特性更加突现。

2.2分帧

分帧就是将n个采样点集合成一个观测单位。设定每帧涵盖的时间是25ms，因为采样率是16000，所以得到每帧的样本点个数是400。另外，为了避免相邻两帧的变化过大，因此会让两相邻帧之间有一段重叠区域。设定的重叠区域是15ms，所以就是每隔10ms取一帧。

2.3对每一帧加窗

由于转换时会将帧内信号当作周期信号处理，所以在帧的两个端点处会发生突变，转换出来的频谱与原信号频谱差别很大。所以要对每一帧加窗，使帧内信号作傅里叶变换时的两个端点处不会发生突变。

2.4对每一帧补零

由于要对每一帧信号进行傅里叶变换，而傅里叶变换要求输入数据长度为一定值，现在一帧为400个采样点，所以补零至最接近的512位。

2.5各帧信号的傅里叶变换

对分帧加窗后的各帧信号进行512点的傅里叶变换得到各帧的频谱。并对语音信号的频谱取绝对值或平方得到语音信号的功率谱。

2.6梅尔滤波

40个三角滤波器在梅尔谱上均匀分布，每两个滤波器间有50％的重叠部分。所以要先把实际频率转换成梅尔频率，实际频率最小为0hz，最大为16000/2＝8000hz。转换成梅尔频率后，计算这40个三角滤波器的梅尔频率分布，然后把梅尔频率转换成实际频率。

2.7取对数

三角窗滤波器组的输出求取对数，可以得到近似于同态变换的结果。

2.8离散余弦变换(dct变换)

对对数能量梅尔谱进行dct变换，取前13维输出，得到梅尔倒谱。

2.9归一化

对所有的梅尔倒谱归一化。先求出所有倒谱向量的均值向量，再用每一个倒谱向量减去均值向量，得到梅尔频率倒谱系数输出特征向量。

s3将已有的若干个乐器对应的音频特征向量和所有的音频帧对应的特征向量输入至朴素贝叶斯模型，根据乐器出现在乐曲中的概率对乐器进行识别。

如图5所示，步骤s3的具体操作过程为：

s3.1将若干个乐器集合c＝{y1,y2,…,yj,…,yn}对应的特征向量，j∈n；和音频帧对应的特征向量输入至经过预训练的朴素贝叶斯模型；

s3.2采用朴素贝叶斯模型的输出公式计算p(y1|xi),p(y2|xi),…,p(yn|xi)；

s3.3通过公式得到乐器yj出现在乐曲x中的概率。

其中，朴素贝叶斯模型的输出公式为：

其中，xi代表一首乐曲x的某一帧，一共有z帧；yj代表某一种乐器，一共有n种乐器。

由上述过程可以求出每个乐器出现在乐曲x中的概率，由于没有出现在乐曲中乐器的概率不一定完全是零，所以需要给概率设置一个阈值，若乐器出现在乐曲中的概率超过阈值，则判断乐器出现在乐曲中，若乐器出现在乐曲中的概率未超过阈值，则判断乐器没有出现在乐曲中。需要说明的是，阈值的取值需要根据具体的音乐或者普遍标准而定，取值的原则是既要保证去除没有出现在乐曲中的乐器，也要保证出现时间比较短的次要乐器不被去除，可以在对模型进行预训练时对阈值进行调整。

乐曲中使用的乐器包括主要乐器和次要乐器，通过朴素贝叶斯方法模型获得各乐器出现在乐曲中的概率区分主要乐器和次要乐器。出现在乐曲中的概率最高的乐器为主要乐器，其他出现在乐曲中的乐器为次要乐器。通常情况下，乐曲的主要乐器只有一种，但也不排除有一些乐曲是由多种乐器主导演奏的，每个乐器出现的概率相差不多。此处多种只两种或两种以上。所以对于几种乐器出现在乐曲中的概率相差不多的情况需要根据乐曲的风格判断主要乐器和次要乐器，不可一概而论。

如图6所示，经过预训练的朴素贝叶斯模型的预训练过程为：向原始朴素贝叶斯模型输入演奏乐器类型已知的乐曲，乐曲根据朴素贝叶斯模型的输出公式获得某一乐器出现在乐曲中的概率，判断概率是否超过阈值，将判断结果与实际演奏乐曲的类型进行比较，若结果相同，则输入朴素贝叶斯模型为最终输出模型；若结果不相同，则调整朴素贝叶斯模型的输出公式，直至结果相同为止。

通过以上步骤就可以在训练得到朴素贝叶斯模型的基础上，对我们需要识别的乐曲所使用的乐器进行分类，同时因为得到的输出结果是每首乐曲使用每个乐器的概率值，还可以根据需要对结果排序，区分出一首乐曲的主要乐器和次要乐器。

实施例二

基于相同的发明构思，本实施例还公开了一种基于朴素贝叶斯模型的乐器种类识别系统，包括：

预处理模块，用于将待识别的乐曲分为若干音频帧；

特征提取模块，用于提取音频帧中的时域信息、频域信息与倒频域信息以及梅尔频率倒谱系数，形成与音频帧对应的特征向量；

识别模块，用于将若干个乐器对应的音频特征向量和所有的音频帧对应的特征向量输入至朴素贝叶斯模型，根据乐器出现在乐曲中的概率对乐器进行识别。

上述内容仅为本申请的具体实施方式，但本申请的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本申请揭露的技术范围内，可轻易想到变化或替换，都应涵盖在本申请的保护范围之内。因此，本申请的保护范围应以权利要求的保护范围为准。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除