一种函数连接型自适应非线性回声消除方法与流程
 2021-01-28 14:01:11|
2021-01-28 14:01:11| 309|
309| 起点商标网
起点商标网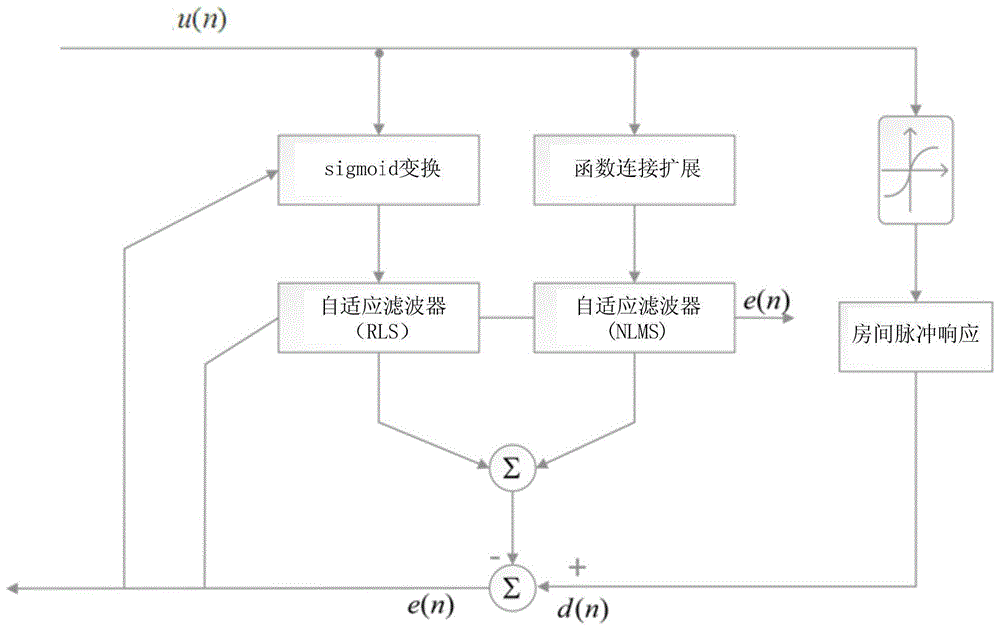
本发明涉及回声对消技术领域,特别涉及一种函数连接型自适应非线性回声消除方法。
背景技术:
近年来,通信和网络技术不断发展,使得人们对通信的质量提出了新的要求,其中最主要的就是语音通话质量。声学回声是降低语音通话质量的重要因素之一。回声是由于麦克风和扬声器之间的回声路径的脉冲响应耦合效应而产生的。由于人耳对回声非常敏感,延迟超过10ms的回声就能被人耳捕捉到,超过32ms的回声就会严重干扰通话质量。因此,如何消除声学回声具有重要的现实意义。目前最普遍应用的方法是基于自适应滤波的回声消除器(acousticechocancellation,aec)。aec的基本原理是运用自适应滤波算法对回声路径的脉冲响应进行估计,其本质是一个系统辨识的问题。然而当回声路径存在非线性的特性时,传统的自适应滤波算法,比如最小均方算法(lms)、归一化最小均方算法(nlms)的性能会出现明显的下降。因此,如何对回声路径中的非线性特性建模,提出有效的非线性回声对消方法具有重要意义。
目前的非线性回声对消的方法中,具有代表性的有以下两种:
(1)用于非线性回声对消的函数连接型自适应滤波器(sflaf)
参考现有方法(1)“functionallinkadaptivefiltersfornonlinearacousticechocancellation”(comminiellod,ieeetransactionsonaudio,speech,andlanguageprocessing,2013,21(7):1502-1512)。该方法的特点是对输入信号进行非线性扩展,具体地说,是通过三角函数函数连接扩展,将未经过变换的信号和经过变换的信号分别用两个滤波器进行滤波,以此达到同时对回声路径的线性和非线性特性建模的目的。
(2)利用sigmoid变换和rls算法结合的非线性回声对消器(rls-sigmoid)
参考现有方法(2)“anonlinearacousticechocancellerusingsigmoidtransforminconjunctionwithrlsalgorithm”(fuj,ieeetransactionsoncircuitsandsystemsii-expressbriefs,2008,55(10):1056-1060)。该方法将回声路径中的非线性变换设定为一种sigmoid变换,在进行滤波之前对sigmoid的参数进行估计,并结合rls的快速收敛和强跟踪能力,能快速使得估计值收敛到真实值。
技术实现要素:
本发明要解决的技术问题是:提供一种函数连接型自适应非线性回声消除方法,用以提升回声对消的效果。
为实现上述目的,本发明采用的技术方案是:将以上的两种方法结合起来,对函数连接型自适应回声对消器做出改进:其中在方法(1)中的sflaf的线性滤波器中引入方法(2)的rls-sigmoid方法,远端输入信号在进行非线性变换时设定为sigmoid类型的变换,并采用rls-sigmoid来估计sigmoid变换的参数值,进一步增强了算法的非线性建模能力,提升了回声对消的效果。
本发明的具体实现方式包括:将回声路径中的远端输入信号分别进行sigmoid非线性变换处理和函数连接扩展处理,将处理后的信号分别通过自适应滤波器进行滤波,并根据滤波结果更新自适应滤波器的权重;其中,sigmoid非线性变换的参数值基于自适应滤波器的滤波结果以及权重估计。
具体的,sigmoid非线性变换公式为:
进一步的,本发明估计sigmoid非线性变换的参数值的步骤可包括:
确定α和β的初始参数值;
将回声路径中的近端输入信号与自适应滤波器的总体滤波值相减后得到残差信号e(n);
基于自适应滤波器的权重、α和β的初始参数值以及残差信号e(n)迭代更新α和β,迭代更新的公式如下;
其中,μα和μβ是α、β在更新时的两个步长参数,t代表转置,n代表时刻,u(n)代表输入信号,ws(n)是滤波器的权重。
进一步的,对于sigmoid非线性变换处理后的信号,自适应滤波器的权重ws(n)利用递归最小二乘算法更新,其更新的公式可如下:
p(0)=δ-1i
ws(n+1)=ws(n)+k(n)e(n)
p(n+1)=λ-1p(n)-λ-1k(n)ut(n)p(n)
其中,矩阵p是逆相关矩阵,i是单位矩阵,k是增益向量,λ和δ分别是遗忘因子和正则化参数。
进一步的,对于sigmoid非线性变换处理后的信号,自适应滤波器的权重wfl(n)利用归一化最小均方算法更新,其更新公式可如下:
其中,μfl和σ分别是步长和正则化参数。。
本发明的有益效果是:本发明将回声路径中的非线性变换设定为sigmoid变换,在函数连接型自适应对消器中引入rls-sigmoid来估计sigmoid变换的参数值α、β。这两种方法的结合与它们各自单独作用相比较,进一步提升了对回声路径的非线性特性的建模能力,收敛速度更快,回声对消的效果更好。
附图说明
图1是本发明实施例的流程框图;
图2是仿真实验中用到的房间脉冲响应。
图3是仿真实验中现有方法(2)和本发明实施例对回声路径中的sigmoid非线性变换的参数的估计过程。
图4是仿真实验中现有方法(1)、(2)和本发明实施例的回升返回损失增强(erle)的对比曲线。
图中编号:s1、s2分别为本发明参数α和β的估计值的迭代曲线,s1、s2分别为现有方法(2)参数α和β的估计值的迭代曲线,d1为本发明的回升返回损失增强曲线,d2为rls-sigmoid的回升返回损失增强曲线,d3为sflaf的回升返回损失增强曲线。
具体实施方式
为了提升回声对消的效果,本发明公开了一种函数连接型自适应非线性回声消除方法,将回声路径中的远端输入信号分别进行sigmoid非线性变换处理和函数连接扩展处理,将处理后的信号分别通过自适应滤波器进行滤波,并根据滤波结果更新自适应滤波器的权重,其中,sigmoid变换的参数值基于自适应滤波器的滤波结果以及权重估计。以下通过实施例和附图对本发明做具体说明。
如图1所示,实施例提供了一种改进的函数连接型自适应非线性回声消除方法,其具体步骤如下:
a、采集远端输入信号
对回声路径中的远端信号进行采样,得到信号当前时刻n的离散值u(n),远端信号在n到n-l+1时刻的值构成当前时刻n滤波器输入向量u(n),u(n)=[u(n),...,u(n-l+1)]t,其中l=300是滤波器抽头数,上标t代表转置;
b、远端信号sigmoid非线性变换
设定sigmoid非线性变换的初始参数值:α(n)=2,β(n)=2;将输入向量u(n)通过sigmoid变换:
c、远端信号函数连接扩展
将输入向量u(n)通过如下的三角函数连接进行扩展:
其中,i、j、q是辅助记号,j、q受限于q,i受限于l,1≤q≤q,q是函数连接扩展的阶数,0≤i≤l-1;得到扩展后的输入信号
d、远端信号滤波
分别将步骤b处理得信号us(n)和步骤c处理得到信号ufl(n)通过自适应滤波器,得到滤波信号:
e、回声抵消
将近端麦克风拾取到带回声的近端信号d(n)与总体滤波值y(n)相减后再回送给远端,回送信号为总残差信号e(n),e(n)=d(n)-y(n)
f、sigmoid非线性变换参数α、β的估计值更新
利用残差信号e(n)对下一次迭代的sigmoid变换的参数按照如下方法进行更新:
其中,μα和μβ是两个步长参数,ws(n)是滤波器的权重;
g、滤波器的权重更新
对于sigmoid非线性变换处理后的信号,自适应滤波器的权重ws(n)利用递归最小二乘算法(rls)更新:
p(0)=δ-1i
ws(n+1)=ws(n)+k(n)e(n)
p(n+1)=λ-1p(n)-λ-1k(n)ut(n)p(n)
其中,矩阵p是逆相关矩阵,i是单位矩阵,k是增益向量,λ和δ分别是遗忘因子和正则化参数;
对于sigmoid非线性变换处理后的信号,自适应滤波器的权重wfl(n)利用归一化最小均方算法(nlms)更新:
其中,μfl和σ分别是步长和正则化参数;
h、令n=n+1,重复a、b、c、d、e、f、g的步骤,直至迭代结束。
仿真实验
为了验证本发明实施例的有效性,进行了仿真实验,并与现有方法(1)(sflaf)和现有方法(2)(rls-sigmoid)进行对比。
仿真实验的远端信号u(n)为由一阶自回归模型(ar)产生,其传递函数为:
按照以上实验条件,用本发明方法实施例与现有的两种方法进行回声消除实验。各种方法的参数具体取值如表1。
表1实验各算法的最优参数近似取值
图3给出了本发明实施例和现有方法(2)对sigmoid非线性变换的参数α和β的估计值的迭代曲线。可以看出,两种方法都能收敛到真实的参数值,而本发明的收敛速度更快。
图4给出了3种方法的回声返回损失增强(erle)的对比曲线。可以看出,由于rls-sigmoid能准确估计sigmoid非线性变换的参数值,其效果要优于sflaf。而本发明在rls-sigmoid的基础上与sflaf结合,进一步加快了sigmoid非线性变换参数值的收敛过程。因此,相较于现有方法(1)、(2)的方法,本发明实施例收敛速度更快,且收敛稳定后的erle值也更大。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



