基于量化误差熵的多层随机神经网络的城市噪音识别方法与流程
 2021-01-28 13:01:36|
2021-01-28 13:01:36| 271|
271| 起点商标网
起点商标网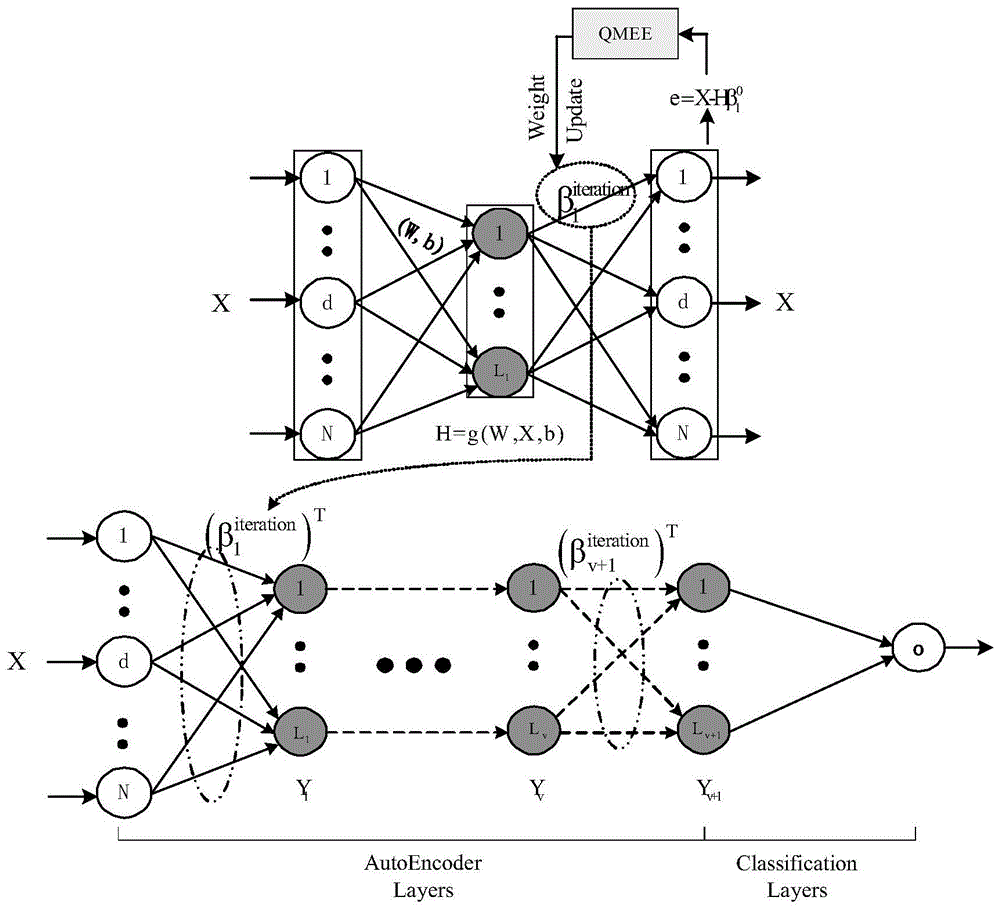
本发明涉及一种基于量化误差熵的城市噪音识别方法,涉及信号处理、语音识别、模式识别、信息熵、误差熵以及随机神经网络等多种技术领域。
背景技术:
随着中国社会经济的快速发展,城市化进程不断加速,在城市化建设的施工过程中产生了大量的噪声,其对居民的日常生活、学习以及身体健康造成较大程度的影响,对噪音的投诉问题也越来越频繁,直接或间接的影响了社会的安定与秩序,因此噪音的识别和管理显得越来越重要。现代技术的发展使得与环境和机械工程施工有关的声学信号可以被收集,人们希望通过信息科学和人工智能等领域的技术能够对环境声音进行有效的识别。在城市噪音识别的过程中通常会考虑到干扰声音的影响,但却很少考虑采集设备中噪音的存在。在数据在采集的过程中,电子元器件会受到电视广播发射器、雷达和无线通讯等设备所产生的电磁脉冲辐射的影响,同时传感器等电子元器件在开关状态切换的时候会产生短时脉冲,加上环境噪音、工频干扰、现场温度变化导致的零点漂移等因素会让采集得到的数据中包含诸多非高斯噪声,使得分类结果难以达到理想状态。
从最优滤波开始,均方误差(mse)已经成为了包括人工神经网络在内的所有自适应系统训练中的一个普遍准则,其主要原因是分析的可追踪性和二阶统计量可以充分描述现实生活中的随机现象的假设。高斯概率密度函数仅由一阶和二阶统计量决定,但在处理非线性系统时还需要考虑系统和信号的高阶统计量。熵是源于物理学的基本概念,后来c.e.shannon在信息论中引入了信息熵的概念。1984年c.e.shannon为解决通信工程中不确定的信息的编码和传输问题创立了信息论,提出了信息的统计定义和信息熵、互信息等概念,解决了信息的不确定性度量问题,并在此基础上对信息论的一系列理论和方法进行了严格的推导和证明,使以信息论为基础的通信工程获得巨大的发展,同时熵作为最优准则扩展了mse。当熵最小化时,误差概率密度函数所有矩(不仅仅是二阶矩)都会受到约束,而最小均方误差只是简单地限制实际输出信号和期望信号之间的平方差,因此我们采用量化误差熵作为一种更为稳健的训练准则,在神经网络训练的过程中代替mse。
技术实现要素:
针对上述背景和存在的问题与不足,为了提高城市噪声类别的识别率,本发明提出了一种基于量化误差熵的多层随机神经网络的城市噪音识别方法。本发明的模型是由一层基于极限学习机的自动编码器(elm-ae)和极限学习机分类器组成的多层随机神经网络,其中自动编码器的隐藏层的输出权重β通过量化最小误差熵作为训练标准,经过梯度下降的方式得到。
qmee算法可以很好的抑制非高斯噪声,又因为传统的分类算法,其模型训练速度缓慢,泛化能力弱,所以我们采用了算法简单、无需反向迭代、计算速度快,泛化能力强的随机神经网络框架,并在模型的编码层加入qmee算法作我们编码层的训练准则,加上编码层对数据有一定的去噪能力,可以让我们的噪音识别更准确。
为实现上述目的,本发明采用了以下技术方案,所述方法包括以下步骤:
步骤一.对采集到的声音信号进行处理,然后进行特征提取,建立声音数据库。
步骤二.将最小量化误差熵引入到多层随机神经网络的编码器中,作为输出权重的训练准则,学习数据中的特征。
步骤三.确定多层随机神经网络的网络结构和参数,将建立的声音数据库中的数据作为多层随神经网络的训练数据。
步骤四.为了模拟城市环境的复杂性,引入非高斯噪声模型。
步骤五.生成非高斯噪声数据,加入到原始数据中,然后放入模型中进行训练。
所述步骤一的具体流程如下:
1-1.采集城市里工程机械设备作业环境中的声音信号,并建立同类型的声音数据库,一共采集了11种类型的声音数据,分别是挖掘机、电锤、切割机、引擎、警报、液压锤、铣床、发电机,歌声,人声,风噪声。
1-2.对声音数据库所有声音数据进行预加重,预加重处理就是将声音信号通过一个高通滤波器:h(z)=1-μz-1,其中μ的取值范围为0.9~1.0。
1-3.然后对处理后的声音数据进行分频处理,帧长一般取10~30ms。
1-4.将每一帧数据乘以汉明窗,以增加帧左端和右端的连续性。假设分帧后的信号为s(n),n=0,1,2,...,n*-1,其中n*为帧的大小,进行汉明窗处理可表示为s′(n)=s(n)×w(n),s′(n)为经过汉明窗处理后的声音数据,w(n)采用下面的函数:
不同的a值会产生不同的汉明窗,一般情况下a取值为0.46。
1-5.对经过汉明窗处理的每一帧声音数据进行快速傅里叶变换(fft),将时域数据转为频域数据。变换公式如下:
1-6.对每一帧fft后的声音数据计算谱线的能量
e(k)=[s(k)]2(3)
1-7.把求出的每帧谱线能量谱通过mel滤波器,并计算在mel滤波器中的输出对数能量s(m)。
三角滤波器的频率响应定义为:
且满足
1-7.将每个滤波器组的输出对数能量s(m),经过离散余弦变化(dct)得到mfcc系数c(n*)。
l为mfcc倒谱系数的个数,基于mfcc计算倒谱系数,即所求的声音特征,对不同机械的声音特征进行标号,建立声音数据特征库。
所述步骤二的具体流程如下:
2-1.误差熵的定义为:
v2(e)称为二阶信息潜能(informationpotential)。fe(ξ)为误差的概率密度函数,ξ为随机误差变量。
2-2.概率密度函数难以直接得到,所以需要对概率密度函数进行估计。概率密度函数的估计方法分类两大类:参数估计和非参数估计。参数估计是已知概率密度函数,但其中部分参数或者全部参数未知,其主要方法又有两类:最大似然估计和贝叶斯估计。非参数估计就是概率密度函数的形式也未知,而是用样本把概率密度函数数值化的估计出来。
2-3.在误差熵和量化误差熵采用的都是核函数
2-4.设线性系统f(z)=wtz,w为线性模型的权重,z为输入数据,数据的大小为n,其误差为ei=ui-wtzi,zi为第i个输入,ui为第i个期望输出。我们希望误差的尽可能的小,即
其中wn为第n次迭代的权重值,η为学习率。
2-5.但是在误差熵的计算过程中,因为要计算误差对ei和ej,在计算较大的数据的时候,其过程会非常的缓慢,所以我们采用了量化误差熵作为训练准则,这样可以减少计算负担,加快计算速度。
2-6.误差的量化过程:
a)误差样本e=[e1,e2,...,en],设定量化阈值ε;
b)初始化:量化码表c。初始化码表c1={e1},其中c1代表第一次迭代后的码表。
c)进行循环i=2,...,n
d)计算ei和ci-1之间的距离dist(ei,ci-1)=|ei-ci-1(j*)|,其中j*=argmin|ei-ci-1(j)|代表ci-1中的第j个元素,|ci-1|代表ci-1中的元素个数。
e)如果dist(ei,ci-1)<ε,则保持码表不变,即ci=ci-1,将ei量化到最近一次循环得到的码表中,q[ei]=ci-1(j*)。否则,更新码表ci={ci-1,ei},并将ei量化为自身q[ei]=ei。
f)重复步骤c)d),直到i>n则停止。
2-7.量化后的信息潜能:
其中m为量化后的误差维度,mm为量化到cm的误差样本数量,cm为码表c中的第m个元素,其满足
2-8.对
其中
2-9.令
2-10.设定梯度上升的迭代次数,实验证明通常30~100次迭代即可得到最优权重。随机神经网络的隐藏层和输出层之间可以看作线性系统,将量化最小误差熵作为其训练准则,来学习数据中的特征
所述步骤三的具体流程如下:
3-1.给出一个训练集
3-2.初始化编码层的输入权重w1i、偏置b1i和输出权重β0,分类层的输入权重w2i和偏置b2i,计算出编码层中隐藏层的输出h(wti,xi,b1i)=g(w1ixi+b1i),其编码层的输出权重通过量化误差熵的方法进行计算,其初始误差e=x-h(w,x,b)β0。
3-3.对误差e按步骤2-6的方法进行量化。
3-4.通过n次迭代,得到最优的输出权重βn
其中1<ic≤n,ic代表第ic次迭代。,实验证明通常30~100次迭代即可得到最优权重。
3-5.计算编码层的输出y1
y1=g(βnx)
3-6.计算本发明中多层随机神经网络的分类层输出权重
3-7.计算网络的输出并识别出城市噪音数据的种类,得到其分类精度。
所述步骤四的具体流程如下:
4-1.为了更真实的体现环境中噪声的复杂性,在特征提取过后得到的数据中加入非高斯噪声。
4-2.在信号处理领域,大多数理论和技术都是在服从高斯分布下取得的,然而实际信号的统计特征并不总是符合高斯假设,我们采用了α稳态分布作为我们的非高斯噪声信号模型。
4-3.稳定分布能够描述多个独立同分布随机变量的分布中微小随机因素的影响,α稳定分布是唯一满足稳定率的分布,在自然科学和工程技术中获得了广泛的应用。α稳定分布作为非高斯噪声模型既可以满足随机噪声产生过程的合理假设又计算方便,α稳定分布的概率密度函数并没有统一的闭合形式,若一个随机变量x服从α稳态分布,可以用以下函数描述:
φ(t)=exp{jδt-γ|t|α[1+jβsgn(t)ω(t,a)]}
其中-∞<δ<+∞,γ>0,0<α≤2,-1≤β≤1。δ表示位置参数,γ代表尺度参数,β为偏斜因子,sgn(t)是符号函数,ω(t,a)代表关于t和α的函数,α表示特征值数,表征α稳定分布概率密度函数拖尾的厚重程度,当β=0、δ=0、α=2时为高斯分布。
4-4.α稳定分布具有如下特点:
a)衰减的速度和α的大小相关,α越小,分布的拖尾越严重;
b)当α≤1时,分布具有无限的均值和方差;
c)分布可以具有不对称分布,β为偏斜因子;
d)参数的取值范围:
所述步骤五的具体流程如下:
5-1.用上面的α稳定分布模型生成α分别等于0.5、0.75、1.0、1.25、1.5,幅值范围为[-1,1]的噪声数据。
5-2.将生成的噪声加入到原始的数据中,然后再放入我们的网络模型中训练。
本发明有益效果如下:
运用基于最小误差熵的多层随机神经网络模型,可以通过量化误差熵对数据采集过程中的噪声起到抑制作用,可以减少数据中的噪声对分类结果的影响,增强模型的鲁棒性。声音数据在mlelm网络中的识别率为91.23%,而在我们提出的qmee-mlelm中的分类正确率为92.85%,提升了1.62%。在数据集中加入了α为0.5、0.75、1、1.25、1.5的非高斯噪声后,mlelm的分类结果分别为:84.23%、82.28%、85.86%、84.96%、85.23%;在我们提出的qmee-mlelm网络中的分类结果分别为:88.31%87.10、89.93%、89.58%、90.10%。相比mlelm最大可提升4.87%的分类准确率,同时体现了我们提出的网络鲁棒性更好。
附图说明
图1为qmee-mlelm框架图
图2为不同阶的α稳态分布图
图3为未加噪声分类结果图
图4为加入不同阶噪声后的分类结果图
具体实施方式
下面结合附图详细说明本发明的具体实施方式:
如图1-4所示,本发明的第一个主要步骤,其步骤如下:
1-1.采集不同的声音信号,并建立声音数据库。
1-2.对原始声音数据进行预加重。
1-3.对数据进行分帧。
1-4.对数据进行加窗处理。
1-5.对数据进行快速傅里叶变换。
1-6.将数据通过三角带通滤波器。
1-7.计算通过滤波器后的对数能量,然后进过离散余弦变换得到mfcc系数。
本发明第二个主要步骤是对误差的量化,其步骤如下:
2-1.设定量化阈值ε,初始化量化码表。
2-1.计算一个误差与码表中每一个值之间的距离,取其中的最小值。如果该值小于量化阈值保持码表不变,否则更新量化码表。
2-3.重复量化的步骤,直到量化过程结束,得到量化后的误差向量。
本发明第三个主要步骤是对,其步骤如下:
3-1.初始化自动编码器的输入权重w、b,并计算其经过激活函数后的隐藏层输出h(w,x,b)。
3-2.在自动编码器中的误差e=x-hβ,用量化最小误差熵作为训练准则,经过一定的迭代次数后,得到最优的输出权重β。
3-3.β和输入样本相乘,在经过激活函数的非线性映射,得到的数据作为分类层的输入样本。
3-4.初始化分类层的输入权重和偏置,得到分类层中的隐藏层的输入,在通过求逆运算得到分类层中输出层的权重。
3-5.通过输出的权重,得到实际输出。在与期望输出进行比较,得到模型的分类的准确率。
本发明第四个主要步骤是对数据进行加噪,其步骤如下:
4-1.用α稳态分布模型生成不同阶的噪音数据。
4-2.将噪音数据加到原始数据上,生成新的训练数据。
本发明第五步骤为模型对加噪后的数据进行训练,输出分类结果,其步骤如下:
5-1.将加噪后的数据放入模型中进行训练。
本发明所述的方法应用城市噪音的识别,使用了多层随机神经网络模型,通过qmee训练准则得到编码层的输出权重,然后通过随机神经网络分类层得到分类结果,可以对城市噪声进行更准确的识别。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



