一种基于盲源分离的水声信号高斯/非高斯噪声抑制方法与流程

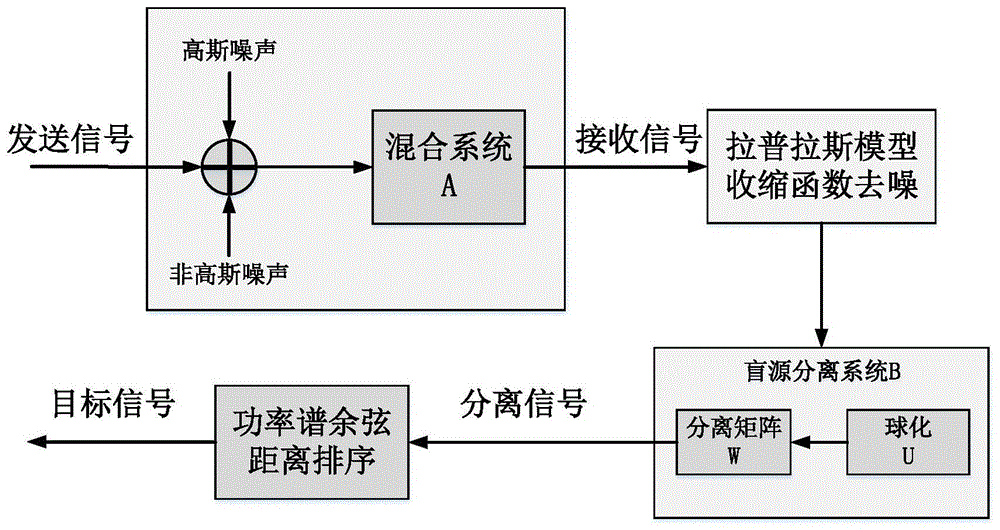
本发明属于水声信号去噪领域，具体地说，涉及一种基于盲源分离的水声信号高斯/非高斯噪声抑制方法。

背景技术：

水下无线数据传输技术是建设海洋强国的关键技术。声波是目前唯一可以在水下远距离传播的信息载体，被广泛应用在水下通信领域。然而，声波在水下传输时，受到大量复杂背景噪声影响。水声噪声的来源可以划分为两种，第一种是人类活动引起的，如船舶航运、工业活动等机器声，第二种是自然因素引起的，如雨、海洋生物和地震活动等产生的噪声。

基于自适应噪声、互信息、排列熵和小波阈值的完全集成经验模态分解的水声信号去噪新方法，这种方式能较好的抑制大的噪声分量，但是计算复杂度较高；基于集成经验模态分解、独自分量分析(independentcomponentanalysis，ica)和小波阈值去噪的信号去噪方法，可降低噪声对信号的影响，但是盲源分离问题往往伴随对分离后源信号顺序不确定等问题；针对卷积混合模型，将时域带噪信号转化为频域进行分离，达到降噪目的，并解决了分离后信号顺序不确定问题；代数优化方法已经用于求解ica目标函数，并基于余弦距离对分离后信号进行排序，具有较高的准确性；然而，实际水声环境中，有用信号和噪声信号通常为非高斯信号，具有较小的负熵，基于负熵的ica方法分离效果较差。且水声通信系统对能量消耗敏感，高复杂度的ica算法难以适用实际水下工程；根据水声信道的稀疏性，采用拉普拉斯分布代替负熵运算，实现了有效信号与非高斯噪声的区分，且降低了基于负熵算法的计算复杂度；基于代数迭代优化算法优化ica目标函数，一定程度上降低了算法计算复杂度。

总体来看，当前水声信号去噪方法仍然存在去噪不彻底、算法复杂度高、得到的目标信号顺序不确定性等问题。

技术实现要素：

本发明的目的是提出一种基于盲源分离的水声信号高斯/非高斯噪声抑制方法，以弥补现有技术的不足。

为实现上述发明目的，本发明采用下述技术方案予以实现：

一种基于盲源分离的水声信号高斯/非高斯噪声抑制方法，其特征在于，包括以下步骤：

s1：获取待去噪的含高斯/非高斯噪声的水声信号；

s2：抑制高斯噪声，得到不含高斯噪声的水声信号；

s3：对s2处理后的水声信号进行盲源分离，得到分离后源信号，即非高斯噪声和目标水声信号；

s4：基于相关系数矩阵确定s3中分离后源信号中的目标水声信号，从而去除非高斯噪声，最终得到高斯/非高斯去噪后的水声信号。

进一步的，所述s1具体如下：

s1-1：信号接收模型：

假设水声通信系统模型采用一发多收模式，发送目标信号为s0(t)，将信道中的非高斯噪声信号视为n-1维非高斯信号[s1(t),s1(t),...,sn-1(t)]^t，接收阵元个数为n，则接收端收到的信号为：

x(t)＝h(t)[s0(t),s1(t),s2(t),...sn-1(t)]^t+e(t)

其中，h(t)表示信道参数，e(t)表示高斯噪声，[g]^t表示转置。

进一步的，所述s2中基于稀疏编码理论抑制高斯噪声。

更进一步的，所述s2具体如下：

s2-1：信号归一化处理：

对接收信号x(t)＝[x1,x2,...,xn]^t归一化处理，处理过程如下所示：

其中，xi为x(t)的分量，i＝1,2,...,n，σ1和分别为x(t)的标准差和均值；归一化后数据表示为x′；

s2-2：求解拉普拉斯稀疏惩罚函数的收缩函数：

拉普拉斯的概率分布如下所示：

其中，s＝e{x′²}，e{x′²}表示求x′²均值；由于水声信号的稀疏性和非高斯性，采用极大似然估计，最大化信号的非高斯性，去除高斯噪声；对p(x′)取对数，得：

l(x′)＝lnp(x′)

对x′求导得：

s2-3：求解极大似然估计情况下信号的稀疏分量，去除高斯噪声；

极大似然估计表达式如下所示：

m(x′)＝sign(x′)max(0,|x′|-σ²|l'(x′)|)

其中sign(g)为符号函数，由下式给出：

将上式代入极大似然估计表达式，得到去除高斯噪声后信号：

式中σ²表示x′中高斯噪声方差，x″是去除高斯噪后的信号；其中x″为归一化信号；为便于s3处理，需对x″进行部分还原，使其仅保持0均值特性，还原过程如下：

x″′＝σ1x″

其中σ1为x(t)的标准差，x″′为基于稀疏编码去噪后信号。

进一步的，所述s3中基于改进灰狼算法优化独立分量分析方法对信号进行盲源分离。

更进一步的，所述s3具体如下：

s3-1：对信号进行白化预处理:

白化可去除信号之间的相关性，同时能够简化后续独立分量提取过程并增强算法的收敛性，白化后的向量z＝(z1,l,zm)^t要求满足e{zz^t}＝i，i为单位矩阵；因此对s2输出信号x″′乘以下式所示白化矩阵：

w0＝λ^-1/2u^t

其中u和λ分别代表x″′的协方差矩阵cx的特征向量矩阵和特征值矩阵，白化后信号为：

xwhite＝w0x″′

s3-2：基于峭度最大化分离源信号:

峭度可描述信号非高斯特性，基于独立分量分析(ica)算法，通过最大化分离后信号峭度，分离源信号，定义随机信号x的峭度如式下所示：

kurt(x)＝e{x⁴}-3(e{x²})²

其中，e{g}表示求期望；传统基于牛顿迭代法的求解过程计算复杂度大，因此基于群智能优化理论，采用改进灰狼算法求解ica问题，通过最大化信号峭度，获得最优分离矩阵w；适应度函数如下所示：

fit＝|kurt(wxwhite)|

其中|g|表示绝对值；

s3-3:基于改进灰狼算法优化独立分量分析方法:

为提高灰狼算法优化性能基于混沌映射初始化种群，提高初始种群个体的多样性和计算效率，然后基于逆不完全γ函数修改狩猎模型，提高算法的探索与开发能力，具体步骤如下：

第一步：初始化种群，利用混沌系统的周期性、随机性和规律性等特点，基于混沌映射初始化种群，即初始分离矩阵wt＝[wt1,wt2,...,wtn]，其中t表示迭代次数，t＝0时，w0表示初始种群，w01,w02,...,w0n表示初始个体，n为种群大小；本发明采用iterative混沌序列产生灰狼的初始位置，iteraive映射的映射方程如下所示：

其中w01是随机生成的分离矩阵，w0(k+1)是经过iteraive映射之后生成的初始分离矩阵，k＝1,2,...,n，b是控制参数，b∈(0,1)；

第二步：基于改进收敛因子的狩猎模型，当迭代次数为t时，计算种群内个体适应度值，根据适应度值保留前三个最大适应度值对应的个体位置，分别记作群体最优个体为wtα，次优个体为wtβ，第三最优个体为wtδ；随机挑选种群中个体wtk，k＝1,2,...,n，并根据wtα、wtβ、wtδ更新产生下一代个体，更新规则如下所示：

其中a1,a2,a3、c1,c2,c3分别是wtk对应wtα、wtβ、wtδ的系数向量，a1,a2,a3和c1,c2,c3分别由下式确定：

其中r1i,r2i在[0,1]范围内随机取值，a为收敛因子；本发明基于逆不完全γ函数改进收敛因子a：

其中amax＝2，最小值amin＝0，tmax是最大迭代次数，λ是随机变量，λ≥0；

第三步：收敛条件，当算法达到最大迭代次数tmax，或者满足下式时，根据当代最优个体wtα输出最优分离矩阵wopt＝wtα；

||wtα-w(t-1)α||2＜σ

其中||g||2表示求二范数，σ一般取值为σ＝10^-7；分离矩阵wopt确定之后，分离后信号表示为下所示：

y'(t)＝woptxwhite。

进一步的，所述s4具体如下：

s4-1：计算分离信号和观测信号的相关系数矩阵：

定义第i个分离后的独立分量y'i(t)对第j个观测数据分量xj(t)的相关系数矩阵为：

其中cij表示向量y'i(t)和xj(t)的协方差矩阵，cii和cjj分别为y'i(t)和xj(t)的方差矩阵；计算相关系数矩阵p得：

其主对角线元素相等且值为1，副对角线元素pi,j相等且取值范围在[-1,1]内,当且仅当y'i(t),xj(t)互相独立时为0；

s4-2：对分离后信号进行排序和相位调整：

首先分别选出矩阵p中各行元素中除主对角线之外的绝对值最大的元素pi，j，且每列也只能取一个元素，若有同一列出现了两个行的最大绝对值，那么选取较大的绝对值元素所在的列，并排除这一列，在剩下的列中再运用相同的方法进行排序，直到将各行相应的排序依据都选出来；

依据选出的排序标记进行排序，具体准则为各行选定的绝对值最大者所在的列即为重新排序后信号所处的位置。

本发明保证了目标源信号的可靠性，最终实现短时间、高准确率的水声信号分类去噪，得到顺序正确的源信号。

本发明的优点和技术效果如下：

本发明根据水声信号的稀疏性，首先基于拉普拉斯分布的稀疏模型，利用其收缩函数，可有效抑制高斯噪声；其次基于改进灰狼优化算法提高ica方法分离性能，同时基于分离后的信号之间的相关系数对分离后信号排序，提取水声目标信号，可有效去除非高斯噪声。本发明能够降低高斯/非高斯复杂海洋噪声对水声信号质量的影响，大幅度提升水声接收信号质量。

附图说明

图1是本发明的一种实施例的整体模型图；

图2是本发明的一种实施例的技术路线图；

图3是本发明的一种实施例中的整体流程图；

图4是本发明的一种实施例中改进灰狼优化算法的流程图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下将结合附图和实施例，对本发明作进一步详细说明。

实施例1：

声波在水下传输时，发送信号受噪声影响，水声通信质量降低，噪声的复杂性和随机性增加了对接收信号的去噪难度，使用单一的信号去噪方式不易完全去除信号的多种复杂噪声，根据噪声特点对噪声进行分类去除，能够保障噪声去除的有效性，得到准确的目标信号，具体模型如图1所示。

基于优化算法的信号盲源分离技术具有较好的信号分离性能，其主要步骤为：首先使用优化算法得到一个分离矩阵，用分离矩阵乘以接收信号得到分离信号。但水下噪声复杂，当前水声信号去噪方法存在去噪不彻底、算法复杂度高、得到的目标信号顺序不确定等问题。如何找到快速收敛的优化算法、并降低盲源分离算法计算复杂度以及对分离后信号的排序，是本实施例所要解决的技术问题。

本实施例提出了一种基于盲源分离的水声信号高斯/非高斯噪声抑制方法，其技术路线图如图2所示，包括以下步骤：

s1：获取待去噪的含高斯/非高斯噪声的水声信号,具体步骤如下：

s1-1：信号接收模型：

假设水声通信系统模型采用一发多收模式，发送目标信号为s0(t)，将信道中的非高斯噪声信号视为n-1维非高斯信号[s1(t),s1(t),...,sn-1(t)]^t，接收阵元个数为n；则接收端收到的信号为：

x(t)＝h(t)[s0(t),s1(t),s2(t),...sn-1(t)]^t+e(t)

其中，h(t)表示信道参数，e(t)表示高斯噪声，[g]^t表示转置。

s2：基于稀疏编码理论抑制高斯噪声，得到不含高斯噪声的水声信号,具体步骤如下：

s2-1：信号归一化处理：

对接收信号x(t)＝[x1,x2,...,xn]^t归一化处理，处理过程如下所示：

其中，xi为x(t)的分量，i＝1,2,...,n，σ1和分别为x(t)的标准差和均值。归一化后数据表示为x′；

s2-2：求解拉普拉斯稀疏惩罚函数的收缩函数：

拉普拉斯的概率分布如下所示：

其中，s＝e{x′²}，e{x′²}表示求x′²均值；由于水声信号的稀疏性和非高斯性，采用极大似然估计，最大化信号的非高斯性，去除高斯噪声；对p(x′)取对数，得：

l(x′)＝lnp(x′)

对x′求导得：

s2-3：求解极大似然估计情况下信号的稀疏分量，去除高斯噪声；

极大似然估计表达式如下所示：

m(x′)＝sign(x′)max(0,|x′|-σ²|l'(x′)|)

其中sign(g)为符号函数，由下式给出：

将上式代入极大似然估计表达式，得到去除高斯噪声后信号：

式中σ²表示x′中高斯噪声方差，x″是去除高斯噪后的信号；其中x″为归一化信号；为便于s3处理，需对x″进行部分还原，使其仅保持0均值特性，还原过程如下：

x″′＝σ1x″

其中σ1为x(t)的标准差，x″′为基于稀疏编码去噪后信号。

s3：基于改进灰狼算法优化独立分量分析方法，并分离s2中不含高斯噪声的水声信号，得到分离后源信号,具体步骤如下：

s3-1：对信号进行白化预处理:

白化可去除信号之间的相关性，同时能够简化后续独立分量提取过程并增强算法的收敛性，白化后的向量z＝(z1,l,zm)^t要求满足e{zz^t}＝i，i为单位矩阵；因此对s2得到信号x″′乘以下式所示白化矩阵：

w0＝λ^-1/2u^t

其中u和λ分别代表x″′的协方差矩阵cx的特征向量矩阵和特征值矩阵，白化后信号为：

xwhite＝w0x″′

s3-2：基于峭度最大化分离源信号:

峭度可描述信号非高斯特性，本实施例基于ica算法，通过最大化分离后信号峭度，分离源信号，定义随机信号x的峭度如式下所示：

kurt(x)＝e{x⁴}-3(e{x²})²

其中，e{g}表示求期望；传统基于牛顿迭代法的求解过程计算复杂度大，因此本实施例基于群智能优化理论，采用改进灰狼算法求解ica问题，通过最大化信号峭度，获得最优分离矩阵w；适应度函数如下所示：

fit＝|kurt(wxwhite)|

其中|g|表示绝对值；

s3-3:基于改进灰狼算法优化独立分量分析方法:

为提高灰狼算法优化性能，基于混沌映射初始化种群，提高初始种群个体的多样性和计算效率，然后基于逆不完全γ函数修改狩猎模型，提高算法的探索与开发能力，具体步骤如下：

第一步：初始化种群，利用混沌系统的周期性、随机性和规律性等特点，基于混沌映射初始化种群，即初始分离矩阵wt＝[wt1,wt2,...,wtn]，其中t表示迭代次数，t＝0时，w0表示初始种群，w01,w02,...,w0n表示初始个体，n为种群大小；采用iterative混沌序列产生灰狼的初始位置，iteraive映射的映射方程如下所示：

其中w01是随机生成的分离矩阵，w0(k+1)是经过iteraive映射之后生成的初始分离矩阵，k＝1,2,...,n，b是控制参数，b∈(0,1)；

第二步：基于改进收敛因子的狩猎模型，当迭代次数为t时，计算种群内个体适应度值，根据适应度值保留前三个最大适应度值对应的个体位置，分别记作群体最优个体为wtα，次优个体为wtβ，第三最优个体为wtδ；随机挑选种群中个体wtk，k＝1,2,...,n，并根据wtα、wtβ、wtδ更新产生下一代个体，更新规则如下所示：

其中a1,a2,a3、c1,c2,c3分别是wtk对应wtα、wtβ、wtδ的系数向量，a1,a2,a3和c1,c2,c3分别由下式确定：

其中r1i,r2i在[0,1]范围内随机取值，a为收敛因子；基于逆不完全γ函数改进收敛因子a：

其中amax＝2，最小值amin＝0，tmax是最大迭代次数，λ是随机变量，λ≥0；

第三步：收敛条件，当算法达到最大迭代次数tmax，或者满足下式时，根据当代最优个体wtα输出最优分离矩阵wopt＝wtα；

||wtα-w(t-1)α||2＜σ

其中||g||2表示求二范数，σ一般取值为σ＝10^-7，算法流程图如图4所示，伪代码如下；

分离矩阵wopt确定之后，分离后信号表示为下所示：

y'(t)＝woptxwhite

s4：基于相关系数确定s3中分离后源信号的顺序，提取目标水声信号，去除非高斯噪声，最终得到去噪后信号，具体步骤如下：

s4-1：计算分离信号和观测信号的相关系数矩阵：

定义第i个分离后的独立分量y'i(t)对第j个观测数据分量xj(t)的相关系数矩阵为：

其中cij表示向量y'i(t)和xj(t)的协方差矩阵，cii和cjj分别为y'i(t)和xj(t)的方差矩阵；计算相关系数矩阵p得：

其主对角线元素相等且值为1，副对角线元素pi,j相等且取值范围在[-1,1]内,当且仅当y'i(t),xj(t)互相独立时为0；

s4-2：对分离后信号进行排序和相位调整：

首先分别选出矩阵p中各行元素中除主对角线之外的绝对值最大的元素pi，j，且每列也只能取一个元素，若有同一列出现了两个行的最大绝对值，那么选取较大的绝对值元素所在的列，并排除这一列，在剩下的列中再运用相同的方法进行排序，直到将各行相应的排序依据都选出来；

依据选出的排序标记进行排序，具体准则为各行选定的绝对值最大者所在的列即为重新排序后信号所处的位置。

上述方法保证了目标源信号的可靠性，最终实现短时间、高准确率的水声信号分类去噪，得到顺序正确的源信号。

例如，假设源信号为[s1,s2,s3]^t，分离后信号为[y′1,y′2,y′3]^t。计算分离后信号相关系数矩阵如下所示：

则除对角线元素绝对值最大的元素如下所示：

其中，第一行除对角线元素绝对值最大元素为0.98。第二行按照规则应当取0.98，而由于具体实施步骤第一步中“每列也只能取一个元素”原则，将导致第三行只剩对角线元素可取，与具体实施步骤矛盾。因此第二行取第三列数字0.87，第三行取-0.55。调整分离后分离信号如下所示：

y(t)＝[y'3,y'1,y'2]

其中y'3，y'1，y'2分别对应源信号s1,s2,s3；基于此，本实施例对盲源分离后信号y'(t)进行顺序调整后，即可得到对源信号[s0(t),s1(t),s2(t),...sn-1(t)]^t的准确估计[s′0(t),s1(t),s′2(t),...s′n-1(t)]^t，从而选取第一路信号s′0(t)，去除其他信号，作为对目标信号s0(t)的准确估计。

本实施例针对复杂海洋噪声，根据水声信号的稀疏性，基于拉普拉斯稀疏模型，求解收缩函数抑制高斯噪声，并基于ica方法分离接收到的混合信号，同时基于相关系数确定分离后信号顺序，提取期望信号，去除非高斯噪声，最终实现基于盲源分离的水声信号分类去噪方法。

以上所述之实施例子只为本发明之较佳实施例，并非以此限制本发明的实施范围，故凡依本发明之形状、原理所作的变化，均应涵盖在本发明的保护范围内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除