一种基于机器学习的玻璃瓶裂纹检测方法与流程

2021-01-28 12:01:51|

284|

起点商标网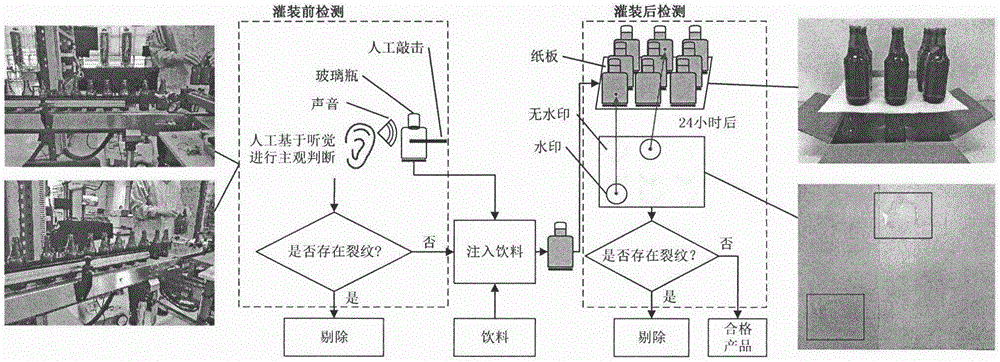

本发明涉及饮料行业中玻璃瓶缺陷的无损检测技术，特别是针对饮料行业中玻璃瓶注入饮料前对空玻璃瓶进行的裂纹无损检测方法。

背景技术：

1.玻璃瓶裂纹检测

饮料行业的玻璃瓶在生产或运输过程中容易发生破损，出现瓶身损坏，产生裂纹等缺陷。这种存在裂纹的玻璃瓶用来装饮料，会造成饮料渗漏导致不必要的浪费，甚至会影响厂家的信誉，从而带来直接或间接的经济损失。这种问题在白酒厂尤其明显，用于灌装白酒的劣质玻璃瓶，不仅会造成白酒的浪费，流入市场更会影响厂家的信誉，造成经济损失。因此，为了防止意外损失，在灌装前对空瓶进行裂纹检查是非常必要的。

目前针对玻璃瓶裂纹可能导致饮料渗漏这一问题，饮料行业通常采用传统的手工检测方法进行玻璃瓶的裂纹检测，如图1所示。这种方法广泛应用于很多饮料厂，如酒厂。该方法由灌装前检测和灌装后检测两部分组成。

灌装前检测是通过人耳的感知(即人的听觉)识别瓶子的缺陷，初步剔除有裂纹的瓶子。这部分旨在通过对瓶子缺陷的初步检测来提高检测效率，其检测准确率约为95％。灌装后检测是将灌装了饮料的玻璃瓶放置在纸板上，24小时后，通过判断纸板上是否有水印来识别对应位置上的玻璃瓶是否存在裂纹。这部分检测准确率接近100％。

总的来说，人工检测方法分类精度可达到100％，但该方法完全依靠人工，存在效率低、占用空间大、浪费饮料等缺点。此外，随着饮料行业从传统的手工作业、手工战术向机械化、自动化、信息化、智能化生产过程迈进，玻璃瓶裂纹检测提出了全自动在线检测和剔除等新的挑战。因此，采用机械代替人工劳动，实现检测的自动化，以降低劳动强度，提高生产效率，保证产品质量。

为了克服这些挑战，结合流水线上酒瓶的生产特点，提出一种自动的检测方法来代替人工检测的灌装前检测，甚至整个人工检测方法。在缺陷检测领域常用的自动检测方法包括基于计算机视觉的方法、基于超声波的方法、基于振动的方法和基于声学的方法。其中，声学检测方法具有操作简单、检测速度快、环境限制小、成本低等优点。该方法首先敲击玻璃瓶，然后采集敲击后产生声学响应——声音，对声音进行分析处理，从而来判断玻璃瓶是否存在裂纹。尽管如此，声学检测方法在实际生产中也存在分类性能低的问题。

2.混洗蛙跳算法

混洗蛙跳算法(shuffledfrogleapingalgorithm，sfla)是eusuff等人在2003年提出一种新型的群体智能优化算法，它模拟了青蛙种群的觅食和迁移过程。整个过程可以描述成如下方式：多只青蛙共同组成了一个大种群，其中又分成了若干个初始子种群，每个子种群包含数只青蛙。每只青蛙的对环境的适应能力都不同。这里用与食物的距离来表示青蛙的适应能力。为了获取食物，每只青蛙都会靠近子种群中距离食物最近的那只青蛙，也就是每只青蛙都会向距离食物最近的青蛙跳跃，从而缩短自己与食物的距离，提高自己的适应能力。当整个青蛙种群完成一次跳跃后，不同的青蛙之间会进行信息交换与共享，目的是提高整个青蛙种群的适应能力。在子种群中，为了避免青蛙积聚在同一位置，每次交换信息之后，要重新形成新的子种群。每只青蛙都携带着各自的信息加入新的子种群。子种群中适应能力最高的青蛙是子种群内部的青蛙的跳跃方向，每次重新生成子种群保证了子种群之间的信息交互。通过交替进行子种群内部每只青蛙向最优青蛙的跳跃(局部搜索)和所有青蛙子种群之间的重新混洗(全局搜索)，可以保证整个青蛙种群是向着最优的方向前进。

算法的数学描述如下：首先生成由n只青蛙个体组成的初始种群p＝{x1，x2，…，xn}，在生成初始种群之后，首先按照每只青蛙的适应度值进行降序排列，并按照模因分组法对青蛙种群进行分组，将青蛙种群分成p个子种群，每个子种群包含q只青蛙，满足n＝p×q的关系。

模因分组法的规则如下：把第1只青蛙分入第1个子种群中，第2只青蛙分入第2个子种群中，第p只青蛙分入第p个子种群中，然后将第p+1只青蛙分入第1个子种群中，以此类推，直至所有的青蛙都分入了某个子种群中。整个分配过程中青蛙的排序序号y与分组组号k的关系为：

同时标记每组中适应度值最大的为组内最优青蛙xb、适应度值最小的为组内最差青蛙xw以及全局适应度值最大的为整个青蛙种群中的全局最优青蛙xg。

然后对每个子种群中的xw进行跳跃，更新规则如下：

d＝r·(xb-xw)

x′w＝xw+d

其中，r是0到1之间的随机数，d表示青蛙跳跃距离。如果更新后，新的青蛙x′w比原来的适应力强，则代替原来的；如果没有改善，则用xg代替xb进行更新；如果仍没有改善，则随机产生一个新的青蛙取代xw。当每个子种群都完成局部搜索后，将所有的青蛙重新混合并排序，然后重新划分子种群，再进行局部搜索，直到达到预定的收敛条件，例如达到混合迭代次数、指定迭代次数内青蛙没有跳跃等。

3.无损缺陷检测的特征提取与选择

特征提取指通过数学变换或者统计分析的方式，从原始的信号中得到一个或多个参数，这些参数能够代表该信号在某一方面的特性。这些参数被称为该信号的特征，获取这些特征的过程就是特征提取。特征提取用于数据挖掘和模式识别领域，特征提取是其中的关键技术之一。通过特征提取，可以获得信号中能够反映数据特性的参数，提取的特征优劣决定了数据挖掘和模式识别的性能。

在无损缺陷检测领域中，有效的特征提取对于整个检测过程至关重要，因为一组重要而紧凑的特征将使正确检测更加容易。特征提取直接从输入信号中获取相关的判别信息(即缺陷信息)。对于一个有效的系统，从同一类样本中提取的特征应该是相似的。同时，从不同类别的样本中提取的特征应该有很大的不同。因此，这些特征可以有效地表示缺陷信息，从而大大提高分类性能。

传统的声缺陷检测系统特征提取方法有时域法、频域法和小波变换法。包含有量纲的过零率和短时能量特征，无量纲的均值、峰值、方差、均方根值、峰值因子、脉冲因子、裕度因子、波形因子、k因子、峭度以及自相关分析参数等特征。频域特征包括频谱峰值、频谱位置、频谱面积和频谱统计参数等特征。基于小波的特征包括小波包分解和重构后得到的每个节点的能量和方差。

为了更好地表征无损缺陷检测任务中的缺陷信息，需要提取了大量的特征。然而，并不是所有的特征都是显著的，因为其中许多特征可能是冗余的，甚至与分类任务无关。因此，需要从提取的大量特征中，选择显著的且合适维度的特征子集。而特征选择就是原始特征集中选择一个特征子集，其中，特征子集的维度远小于原始特征集维度。特征选择在不改变原始特征集性质的前提下，从中选择一部分特征，组成一个新的特征空间。特征选择的结果直接影响分类器的复杂度、精度以及稳定性。因此，选择合适的特征子集对缺陷检测也很重要。

特征选择旨在提高分类器的分类性能，降低计算复杂度。目前对特征选择方法的研究主要集中于搜索策略和评价准则。按照特征子集的形成过程，特征选择的基本搜索策略可分为以下3种：全局搜索、随机搜索和启发式搜索。全局搜索方法如分支定界法虽然能够得到最优的特征子集，但是存在计算复杂度高等问题。随机搜索方法如relief系列算法具有较高的不确定性，需要进行较多循环，且参数的设置存在一定的困难。启发式搜索如单独最优组合、序列前向选择方法、广义序列前向选择方法(gsfs)，序列后向选择方法(sbs)，广义序列后向选择方法(gsbs)，增l去r选择方法，广义增l去r选择方法，浮动搜索方法等。启发式搜索策略虽然效率高，但是以牺牲全局最优为代价。一个具体的搜索算法会采用两种或多种基本搜索策略，例如遗传算法是基于随机搜索和启发式搜索算法。

特征选择因为搜索空间大和特征之间具有相关性的问题，使其具有很大的挑战性。目前，大量的有效特征选择方法被提出，但是在实际的应用中存在着很多不足。大部分的特征选择方法存在局部最优或者是计算复杂度高的问题。

4.希尔伯特-黄变换(hilbert-huangtransform，hht)

针对非线性、非平稳信号，由于其较强的时变性，一般采用时频分析方法提取信号的特征。信号的时频分析方法能够将信号在时频空间上展开的基础上，对局部分量进行分析，这种方法能够更好地反映音频信号的时频特性。常用的时频分析方法有短时傅里叶变换(stft)、wigner-viller分布(wvd)、小波变换(wt)，这些方法虽然能够较好地分析音频信号的时频特性，但也存在某些问题，如stft存在heisenberg测不准原理和单一分辨率问题，wvd存在严重的交叉干扰项问题，小波变换存在过分依赖小波基选取和能量泄露等限制。

hht是美国nasa的黄锷博士(nordene.huang)在1998年提出的一种时频域分析方法。由于其完全基于信号本身，具有自适应性，对非线性非平稳信号的处理效果好，特别适用于非平稳、非线性信号分析，所以被广泛应用在在海洋信号、地震信号分析、生物医学、健康监测等领域，并取得了不错的成果。hht主要分成两部分，首先对信号进行经验模式分解(empiricalmodedecomposition，emd)得到一系列频率由高到低的本征模式函数(intrinsicmodefunction，imf)，然后对imf分量进行hilbert变换得到有意义的瞬时频率(信号的瞬时属性)。其中每个imf分量必须满足以下2个条件：(1)在整个数据范围内，极值点与过零点的数目必须相等或者最多相差一个；(2)在任意一点处，所有极大值点形成的上包络线和所有极小值点形成的下包络线的平均值始终为零。

emd分解的步骤如下：

1)对于待处理信号x(t)，找出信号的所有局部极大值、极小值点；

2)对这些极值点进行样条插值，得到由所有局部极大值点构成的上包络线和所有局部极小值点构成的下包络线，分别记为u(t)、v(t)；

3)求上下包络线的均值为：

4)令h(t)＝x(t)-m(t)，验证h(t)是否满足imf分量的条件，若满足，则h(t)为第一个imf分量；如不满足，以h(t)为输入继续进行前面的步骤，直至得到第一个imf分量，并将其记为c1(t)；

5)将r1(t)＝x(t)-c1(t)作为新的分析信号，重复步骤(1)到步骤(4)，得到第二个imf分量c2(t)，此时记r2(t)＝r1(t)-c2(t)，重复上述步骤直到得到余项rm(t)是一个单调信号或者其值小于某个预先给定的阈值，分解结束，得到所有的imf分量；

若对得到的每个imf分量进行hilbert变换，得到信号的瞬时频率和瞬时幅度。其中，

hilbert变换用于求取信号的瞬时参数。imf分量c(t)的hilbert变换定义如下：

也就是信号和时间倒数的卷积。对于emd分解后得到的每个imf分量ci(t)进行hilbert变换，得到相应的解析信号：

其中，ai(t)为解析信号的幅值，θi(t)为解析信号的相位。定义信号的瞬时频率为：

从而ci(t)可表示为：

(re表示取实部)

将ai(t)表示在联合的时频平面上，即可得到ci(t)的hilbert谱：

emd分解后的残余分量能量较大，会对于其他imf分量的分析产生干扰，而且信号的信息通常都位于高频分量中，所以在进行hilbert变换时一般会忽略残余分量。

在得到了每个imf分量的hilbert谱之后，可以通过下面的公式求取信号x(t)的hilbert谱：

通过hilbert谱可以定义信号的边际谱：

相比频谱，信号的边际谱能更准确地反映出信号的频率。通过边际谱可以看出一定时间内，信号主要集中在什么频率上。边际谱中某一频率的能量代表着在整个时间轴上，可能有这样一个频率的振动波在局部出现过，其幅值越大，代表该频率出现的可能性越大。

与其他基于傅里叶变换的时频分析方法不同，hht不存在傅里叶谱分析的诸多缺点，如hht可以在没有先验知识的情况下处理任何信号，并且不受heisenberg不确定性原则的限制。

然而，由于hht方法存在虚假imf分量和模态混淆问题，使其对声信号进行精确的分解十分困难。针对上述问题，将wpd与hht相结合的改进hht方法被提出。该方法利用小波包分解方法从声信号中提取一系列的窄带信号以解决模态混叠问题，然后利用emd方法从这些窄带信号中提取出多个imf分量。再基于imf分量与原始窄带信号的互相关性筛选出真实的imf分量，以解决虚假imf分量。最后，通过hilbert变换从实际imf分量中提取瞬时属性，从这些瞬时属性中提取相关的时频特征。

5.互信息

互信息(mutualinformation，mi)是信息论中的一个基本概念，它表示了两个离散变量之间拥有共同信息的含量，可以用于评估这两个变量之间的相似程度和依赖关系。对于两个离散变量x和y，假设它们的边缘概率分布为p(x)和p(y)，则可以通过下面的公式计算它们之间的互信息i(x；y)：

其中，p(x，y)是x和y的联合概率分布。通常情况下，都是通过信息熵来计算两个变量之间的互信息，计算公式如下：

i(x；y)＝h(x)-h(x|y)

其中，h(x)表示变量x的信息熵，它的计算公式如下：

h(x|y)表示x关于y的条件熵，它的计算公式如下：

互信息可以用于表示两个变量之间的依赖程度，当x和y完全独立时，它们之间的互信息值为0，当x和y之间的相似程度越大，互信息的值就越大。

技术实现要素：

本发明所要解决的技术问题是，针对现有人工检测方法存在的完全依靠人工、检测效率低、浪费饮料等问题，提出一种高检测准确率、高效率、更节省人力的玻璃瓶裂纹检测方法。

本发明所采用的技术方案是：一种基于机器学习的玻璃瓶裂纹检测方法，包括如下步骤：

1)采用拾音器采集金属棒敲击待检测的玻璃瓶瓶身产生的声音信号，并将声音信号传输至工控机；

2)在工控机中，对采集得到的声音信号进行特征提取，提取声音信号的传统特征、短时特征和时频特征三大类特征，得初始特征集；

3)采用混洗蛙跳算法对初始特征集进行特征选择，得到最优特征子集；

4)将最优特征子集作为bpnn的输入，进行bpnn训练得到模型参数，然后根据bpnn的输出判断玻璃瓶是否存在裂纹，最终得到裂纹检测结果；

5)根据裂纹检测结果，采用剔除设备剔除存在裂纹的玻璃瓶。

步骤2)所述的采集得到的声音信号进行特征提取，包括：

(2.1)提取声音信号的传统特征，记为{f1}。声音信号的传统特征包括：时域特征、频域特征和时频域特征。其中，时域特征包括：过零率、能量、均值、方差、均方根、峰值、峰值因子、脉冲因子、裕度因子、波形因子、k因子、峭度，以及自相关序列的均方根、峰值和峰值因子。频域特征包括：频谱面积、前5个频谱幅度峰值及其频率位置、重心频率、均方频率、以及频率的均方根、标准方差和方差。时频域特征包括三层小波包分解与重构后得到的第三层所有节点的能量和方差；

(2.2)提取声音信号的短时特征，记为{f2}。先对信号进行分帧处理，得到若干个子帧信号，然后分别提取各个子帧信号的传统特征，将各个子帧信号传统特征组合最终得到短时特征集{f2}；

(2.3)基于改进hht方法提取声音信号的时频特征，记为{f3}。其步骤如下：

(2.3a)采用daubechies小波对输入声音信号x(t)进行n层小波包分解与重构，得到2ⁿ个不同频段的窄带信号；

(2.3b)对得到的所有窄带信号分别做经验模式分解，得到若干个imf分量；

(2.3c)计算窄带信号与其各个imf分量的互信息量，并与imf分量筛选阈值mi对比，筛选出能够反映信号特征的真实imf分量；

(2.3d)将筛选出来的真实imf分量按照频率由高到低的顺序排序，得到最终整个信号的imf分量；

(2.3e)对最终整个信号的imf分量进行hilbert变换，得到信号的瞬时属性，包括：每个imf分量的瞬时频率和瞬时幅度，以及边际谱；

(2.3f)基于信号的瞬时属性，提取声音信号的时频特征，包括：边际谱的频谱面积、带宽、截止频率和方差，前5个边际谱的峰值和峰值位置，边际谱方差，第三个和第四个imf分量的极大值和极小值，前6个imf分量的瞬时幅度的均值、均值、方差和有效值。

步骤3)所述的采用混洗蛙跳算法对初始特征集进行特征选择，包括：

(1)设定混洗蛙跳算法的初始参数，包括：青蛙种群数量、每组数、算法最大迭代次数和迭代次数iter＝0；

(2)设定特征选择中输出的最优特征子集维度m，m对应混洗蛙跳算法中青蛙个体的位置编码位数，其中青蛙的位置对应于维度为n的初始特征集中的一个维度为m特征子集；

(3)根据步骤(1)和步骤(2)设定的参数，随机生成青蛙种群的个体信息，其中每个青蛙个体的位置编码用一个含有m个由0到n-1之间的整数组成的无序不重复的序列表示，序列中的每个数对应一个特征，其中，n是初始特征集维度；

(4)将青蛙个体的位置信息利用适应度函数进行适应度计算，得出青蛙个体的适应度值以及是否满足的优化的约束条件，即计算在特征选择中，该方案对应的特征子集的评估函数值。适应度函数表达式为：

这里s＝{s1，s2，…，sm}是青蛙个体的位置信息，对应青蛙个体表示的特征子集，其中s∈f，si和sj分别表示s中的第i和第j个特征。l表示样本数据对应的目标类标签。i(si，l)表示第i个特征与目标类标签的平均互信息量。i(si，sj)表示第i个特征与第j个特征的平均互信息量。对青蛙种群的每个个体所在的位置进行评估，得到青蛙种群的每个个体适应度值；

(5)按照青蛙个体的适应度值对整个青蛙种群进行降序排序，并按照模因分组法对青蛙种群进行分组，确定每组中的组内最优青蛙、组内最差青蛙以及整个青蛙种群中的全局最优青蛙；

(6)每组中首先利用组内最优青蛙的信息更新组内最差青蛙，若发现更新后的组内最差青蛙的适应度值优于之前的青蛙且满足特征子集的约束条件，则完成一次更新过程；否则，采用全局最优青蛙的位置信息更新，若更新后的组内最差青蛙的适应度值优于之前的青蛙且满足特征子集的约束条件，则完成更新过程；若依然无法更新成功，则采用随机更新的方式更新组内最优青蛙；

(7)迭代次数iter加1；

(8)对全体青蛙种群进行混洗。若迭代次数小于算法最大迭代次数，则转到步骤(5)；否则，输出全局最优青蛙信息；

(6)根据全局最优青蛙信息，得到全局最优解的编码即为最佳的特征子集。

本发明针对具体的玻璃瓶裂纹检测任务，采用改进hht的特征提取方法扩展传统声音特征以提高玻璃瓶裂纹检测的精度，然后采用混洗蛙跳算法优化特征集，以得到更紧凑和显著的特征子集，最后采用bp神经网络对玻璃瓶是否存在裂纹进行决策。本发明可以有效解决饮料行业生产线中现有人工检测方法中存在的过度人力消耗、低检测效率、饮料浪费等问题，从而在保证高精度、自动化地检测玻璃瓶裂纹。相比于传统的人工玻璃瓶裂纹检测方法，本发明提出的玻璃瓶裂纹检测具有检测精度高、效率高的特点。

附图说明

图1是饮料行业现有的玻璃瓶裂纹检测方法示意图。

图2是本发明中改进hht特征提取算法流程图。

图3是本发明中混洗蛙跳算法流程图。

图4是本发明中基于机器学习的玻璃瓶裂纹检测框图。

具体实施方式

下面结合实施例和附图对本发明的一种基于机器学习的玻璃瓶裂纹检测方法做出详细说明。

如图4所示，本发明的一种基于机器学习的玻璃瓶裂纹检测方法，其特征在于，包括如下步骤：

1)采用拾音器采集金属棒敲击待检测的玻璃瓶瓶身产生的声音信号，并将声音信号传输至工控机；

2)在工控机中，对采集得到的声音信号进行特征提取，提取声音信号的传统特征、短时特征和时频特征三大类特征，得初始特征集。该步骤包括：

(2.3)基于改进hht方法提取声音信号的时频特征，记为{f3}。其步骤如下：

(2.3a)采用daubechies小波对输入声音信号x(t)进行n层小波包分解与重构，得到2ⁿ个不同频段的窄带信号；