一种基于极小化极大化的欠定盲源分离方法及系统和装置与流程
 2021-01-28 12:01:40|
2021-01-28 12:01:40| 311|
311| 起点商标网
起点商标网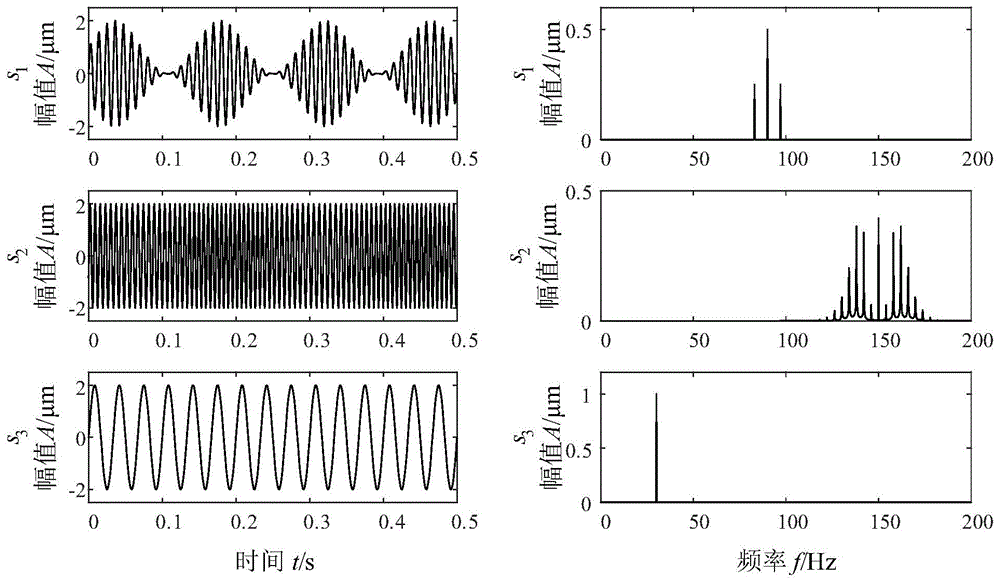
本发明属于机械振动噪声信号处理领域,具体涉及一种基于极小化极大化的欠定盲源分离方法及系统和装置。
背景技术:
燃气轮机等高端装备零部件众多,回转体不平衡运动、转子不对中以及夹装不紧产生的振动加速其与其连接件磨损,严重影响设备性能与寿命,而振动产生的辐射噪声则降低军事装备隐蔽性,严重影响军队作战能力。对燃气轮机等高端装备采取减振降噪措施能够有效抑制振动噪声,燃气轮机等高端装备具有结构复杂精密、振动噪声源众多、结构紧凑的特点,使得识别与定位振动噪声源尤为困难,成为实现减振降噪的技术瓶颈。因此对燃气轮机等高端装备进行振动噪声源识别,精准定位振噪源零部件,揭示其传递混合机制,可以有针对地指导燃气轮机等高端装备的减振降噪。
高端装备内部传感器采集的信号是多个振动噪声源传递至传感器的叠加。但由于燃机等高端装备内部结构精密紧凑,工作环境高温高压,传感器可安装位置少,无法安装足够的传感器。欠定盲源分离能够在缺乏先验知识且传感器数量少于源信号数量的情况下,有效分离出源信号。目前,欠定盲源分离方法主要通过信号在变换域进行聚类提取单源点并估计混合矩阵,然后利用混合矩阵采用l0范数优化恢复源信号,但l0不连续导致恢复的源信号误差很大,无法有效分离舰载燃气轮机等高端装备内部机械混合信号。
技术实现要素:
本发明的目的在于提供一种基于极小化极大化的欠定盲源分离方法及系统和装置,以克服现有技术的不足。
为达到上述目的,本发明采用如下技术方案:
一种基于极小化极大化的欠定盲源分离方法,包括以下步骤:
步骤1)、将采集的若干观测信号做短时傅里叶变换得到时频域复矩阵;
步骤2),对时频域复矩阵进行单源点识别,提取时频域复值单源点;
步骤3),根据步骤2中得到的频域复值单源点,通过层次聚类法对得到的时频域复值单源点进行聚类并估计出瞬时混合矩阵;
步骤4),根据步骤3)中得到的瞬时混合矩阵,对基于非凸罚函数的范数目标函数进行全局寻优,实现频域复值源恢复,最后采用短时傅里叶逆变换将恢复的频域信号变换回时域得到分离信号。
进一步的,步骤1)具体为:采集m个观测信号x(t)=[x1(t)x2(t)…xm(t)]t,其中上标t表示转置,采样时间序列t=1,2,…,t,将采集的观测信号做短时傅里叶变换得到时频域的复矩阵x。
进一步的,通过短时傅里叶变换将每个待分析的时域观测信号xi(t)变换到时频域xi=[xi,1,xi,2,…,xi,j],其中第一维表示频率,第二维表示的是时间;所有的观测信号的时频域为一个三维矩阵x=[xi,j,k]其第一维是观测信号序列,第二维表示时间,第三维表示频率。
进一步的,对时频域复矩阵进行单源点识别,分别取时频域复矩阵x=[xi,j,k]同一时间同一频率的复值向量的实部以及虚部:
其中xj.k=[x1,j,kx2,j,k…xm,j,k]t是时频域复矩阵x=[xi,j,k]第j时刻,第k频段的子向量,re(·)和im(·)分别为取实部算子和取实部虚部算子,将实部与虚部余弦角大于ε的提取为单源点向量,即满足:
进一步的,对得到的时频域复值单源点进行取模并归一化处理使其变为实数向量且模为1,即:
进一步的,利用瞬时混合矩阵
其中
通过梯度下降来进行求解,分别更新目标函数中的v以及y从而实现源信号在时频域的恢复。
进一步的,采用短时傅里叶逆变换,将恢复的时频域源信号变换到时域完成源信号的分离。
进一步的,利用以下公式对分离信号进行性能评价:
其中si为第i个源信号,
一种基于极小化极大化的欠定盲源分离系统,包括数据采集模块、数据预处理模块、混合矩阵处理模块和分离模块;
数据采集模块用于获取待分析设备的观测信号,并将获取的观测信号传输至数据预处理模块;
数据预处理模块对观测信号做短时傅里叶变换得到时频域复矩阵,同时根据时频域复矩阵进行单源点识别,提取时频域复值单源点;
混合矩阵处理模块根据得到的频域复值单源点,通过层次聚类法对得到的时频域复值单源点进行聚类并估计出瞬时混合矩阵,并将瞬时混合矩阵传输至分离模块;
分离模块根据得到的瞬时混合矩阵,对基于非凸罚函数的范数目标函数进行全局寻优,实现频域复值源恢复,最后采用短时傅里叶逆变换将恢复的频域信号变换回时域得到分离信号并输出。
一种基于极小化极大化的欠定盲源分离装置,包括存储器、处理器以及存储在所述存储器中并可在所述处理器上运行的计算机程序,所述处理器执行所述计算机程序时实现如权利要求1所述方法的步骤。
与现有技术相比,本发明具有以下有益的技术效果:
本发明一种基于极小化极大化的欠定盲源分离方法,针对欠定瞬时混合盲分离,首先利用短时傅里叶变换将时域时域线性混合信号转化为时频域瞬时线性混合下每个频带上的分量,此时的时频域信号为复值的,基于混合数据样本的稀疏性以及同源相位一直假设,分别计算同一时频分量复值混合数据的实数向量与虚数向量余弦角,将夹角满足条件的向量提取为单源点向量,通过对提取的单源点向量进行聚类估计出混合矩阵;利用混合矩阵以及源信号的稀疏性假设将源信号恢复问题转化为l1范数优化问题,将源信号在时频域恢复后采用短时傅里叶逆变换将时频域的源信号变换回时域从而实现欠定盲源分离。本发明采用基于极小化极大化算法方法恢复源信号,构建非凸罚函数使目标函数的优化逼近l0范数优化,避免了传统的l1范数正则化的系统性低估及依照稀疏性假设恢复的源信号。并且保证了目标函数的凸性,即在最优解求解过程中不会陷于局部最优解,减少恢复信号与源信号间的误差。
本发明一种基于极小化极大化的欠定盲源分离系统,结构简单,能够根据上述方法快速将源信号在时频域恢复后采用短时傅里叶逆变换将时频域的源信号变换回时域从而实现欠定盲源分离,提高了源信号的分离精度,可以有针对地指导燃气轮机等高端装备的减振降噪。
附图说明
图1为本发明实例1中源信号波形和频谱图;
图2为本发明实例1中混合信号波形和频谱图;
图3为本发明实例1中采用本发明方法分离信号波形及其频谱图;
图4为本发明实例1中所述的l1传统范数优化方法分离信号波形和频谱图。
具体实施方式
下面结合附图对本发明做进一步详细描述:
一种基于极小化极大化的欠定盲源分离方法,使用欠定线性瞬时混合模型,对混合观测信号进行分离,具体包括以下步骤:
步骤1,采集m个观测信号x(t)=[x1(t)x2(t)…xm(t)]t,其中上标t表示转置,采样时间序列t=1,2,…,t,将采集的观测信号做短时傅里叶变换得到时频域复矩阵x;
步骤2,对时频域复矩阵x进行单源点识别,提取时频域复值单源点;
步骤3,根据步骤2中得到的时频域复值单源点,通过层次聚类法对得到的时频域复值单源点进行聚类并估计出瞬时混合矩阵;
步骤4,根据步骤3中得到的估计混合矩阵,对基于非凸罚函数的l1范数目标函数进行全局寻优,实现频域复值源恢复,最后采用短时傅里叶逆变换将恢复的频域信号变换回时域得到分离信号y(t)。
步骤1中通过短时傅里叶变换将每个待分析的时域观测信号xi(t)变换到时频域xi=[xi,1,xi,2,…,xi,j],其中第一维表示频率,第二维表示的是时间;所有的观测信号的时频域为一个三维矩阵x=[xi,j,k]其第一维是观测信号序列,第二维表示时间,第三维表示频率。
步骤2中对步骤1中的时频域复矩阵单源点识别,分别取时频域复矩阵x=[xi,j,k]同一时间同一频率的复值向量的实部以及虚部:
其中xj.k=[x1,j,kx2,j,k…xm,j,k]t是时频域复矩阵x=[xi,j,k]第j时刻,第k频段的子向量,re(·)和im(·)分别为取实部算子和取实部虚部算子,进一步将实部与虚部余弦角大于ε的提取为单源点向量,即满足:
步骤3中对步骤2中的单源点向量进行取模并归一化处理使其变为实数向量且模为1,即:
步骤4中利用步骤3中的估计矩阵
通过梯度下降来进行求解,分别更新目标函数中的v以及y从而实现源信号在时频域的恢复。采用短时傅里叶逆变换,将恢复的时频域源信号变换到时域完成源信号的分离。
利用以下公式对步骤4中利用以下公式对分离信号进行性能评价:
其中si为第i个源信号,
下面通过方阵实验来对本发明做进一步的详细说明。
实例1,选择3个典型机械信号作为源信号,其表达式如下所示:
得到的源信号波形及其频谱图如图1所示,将源信号通过混合矩阵得到观测到的混合信号,观测数目为2,图2为混合信号的波形及频谱图,混合矩阵选择如下式所示。
从图2中可看出,由于源信号的互相叠加,从观测信号的时域波形中很难看出含有何种信号成品,从频谱中虽然可以看出其频率特性,然而由于缺乏先验知识,无法确认哪部分频域来自哪一个源,因此仅靠观测信号无法直接获取源信号的估计。
利用本发明提出的欠定盲分离方法对观测信号进行处理,本实例中短时傅里叶变换窗厂选择为512,窗型为汉宁窗,每次移动步长为256,本发明提出方法得到的分离信号波形和源信号及其频谱图如图3所示,对比图1和图3,可以看出分离信号的波形和和源信号波形极其相似,而且从频谱图对比可知,分离信号中保留了对应源信号的主要特征频率,表明本发明提出方法的准确性和有效性。
本实例中传统l1范数优化方法短时傅里叶变换窗厂为512,窗为汉宁床,窗每次移动步长为256,正则化参数λ=0.55。传统l1范数优化方法得到的分离信号波形和源信号及其频谱图如图4所示,通过图1和图4,对比分离信号和源信号频谱图,传统l1范数优化方法也能从分离出主要特征频率,但由于l1范数优化固有的系统性低估真实信号,源信号3的特征频率被错误的估计到源信号1和源信号2中,使得还原的源信号存在较大误差。
为了定量评价估计恢复信号的准确性,采用下式对估计的源信号进行处理:
其中si为第i个源信号,
经本发明方法得到的分离信号波形相关系数矩阵为:
经过传统l1范数优化方法得到的分离信号波形相关系数矩阵为:
从相关系数矩阵可以看出所提出方法的精度高于传统l1范数方法。
本发明构建了非凸罚函数使目标函数的优化逼近范数优化,避免了传统的范数正则化的系统性低估,保证了最优解求解过程中不会陷于局部最优解,减少恢复信号与源信号间的误差,能有精准有效的分离舰载燃气轮机等高端装备内部机械混合信号,为舰载燃气轮机减振降噪提供重要指导,具有重大工程意义。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 


