自适应反馈有源控制系统水床效应抑制的方法与流程
 2021-01-28 12:01:20|
2021-01-28 12:01:20| 301|
301| 起点商标网
起点商标网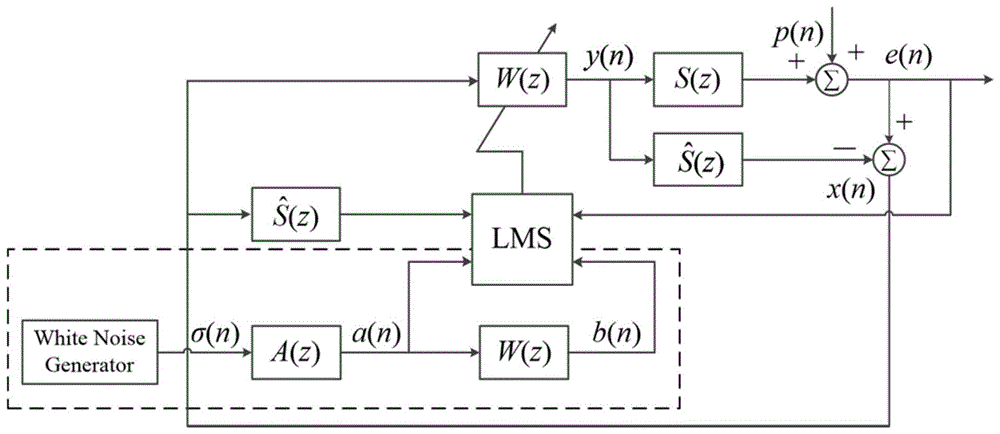
本发明属于有源噪声控制的技术领域,具体涉及一种自适应反馈有源控制系统水床效应抑制的方法。
背景技术:
有源噪声控制(activenoisecontrol)已广泛应用于有源降噪耳机、汽车有源降噪、降低机器噪声、有源声屏障和降低室内噪声等场合,在新兴领域也有应用前景,如降低机器人使用环境的噪声,提高其识别语音的能力。
有源噪声控制结构可分为前馈有源噪声控制和反馈有源噪声控制,其中前者性能依赖于参考信号与初级噪声信号之间的相干性。在许多anc系统的应用场景中,无法获取高质量的参考信号,降噪性能弱或无法降噪,可使用反馈有源控制系统。然而反馈系统存在“水床”效应,即在某特定频段降噪的同时会引起其他频段噪声放大。
针对该问题,人们通常使用离线算法设计控制滤波器,并针对离线算法设计改善水床效应的方法,如rafaely等提出用h2/h∞设计方法(b.rafaelyands.j.elliott,“h2/h∞activecontrolofsoundinaheadrest:designandimplementation,”ieeet.contr.syst.t.7(1),79-84(1999)),构造以“水床”抑制和鲁棒稳定性为约束条件的凸优化问题,再使用序列二次规划算法求解最优滤波器,得到满足约束条件且有效降噪的控制滤波器。如zhang提出一种不需要复杂权重参数选择和优化的数值求解算法,通过尽量展宽噪声放大频段和均匀噪声放大频段内噪声放大量的方法,将噪声放大峰值限制于给定的限值来改善“水床”效应(l.zhang,l.wu,andx.qiu,“anintuitiveapproachforfeedbackactivenoisecontrollerdesign,”appl.acoust.74(1),160-168(2013))。然而这些算法不适用于实时自适应系统。在实时自适应系统,使用泄漏滤波-x最小均方(lfxlms)算法可降低全频段输出信号的大小,可在内模控制(imc)结构的反馈anc系统中实现“水床”抑制,然而该算法仅能对全频段控制滤波器以相同权重约束。已有研究(l.wu,x.qiu,andy.guo,“ageneralizedleakyfxlmsalgorithmfortuningthewaterbedeffectoffeedbackactivenoisecontrolsystems,”mech.syst.signal.pr.106,13-23(2018))提出一种应用于自适应系统的广义泄漏滤波-x最小均方(glfxlms)算法,使用泄漏矩阵代替传统泄漏滤波-x最小均方(lfxlms)算法中的泄漏因子,对特定频段的控制滤波器幅值抑制,来抑制水床效应。然而该算法每次迭代都需要将泄漏矩阵和滤波器向量相乘,即使可通过快速算法进行优化,但计算量依然很大。较大的运算量可能导致较高的系统成本,甚至无法实现,尤其对于多通道系统。
基于此,有必要针对反馈有源噪声控制系统,提供一种可以通过对特定频段的控制滤波器幅值抑制来抑制水床效应引起的噪声放大,且计算量较小的算法。
技术实现要素:
发明目的:为了克服现有技术中存在的不足,本发明提供一种自适应反馈有源控制系统水床效应抑制的方法,与泄漏滤波-x最小均方算法相比,可在自适应反馈有源控制系统中实现对一个或多个特定频段的水床抑制,与现有可对特定频段水床效应进行抑制的算法即广义泄漏滤波-x最小均方算法相比,运算量大幅降低,更利于实用。
技术方案:为实现上述目的,本发明采用的技术方案为:
一种自适应反馈有源控制系统水床效应抑制的方法,包括如下步骤:
步骤1,测量有源控制系统次级路径传递函数单位冲激响应,得到次级路径传递函数的估计向量
步骤2,根据需要抑制水床效应的频段设计频谱整形滤波器a(ω)的幅频响应,在需要抑制的频段频谱整形滤波器a(ω)的幅值大于其他频段的幅值,并根据需要抑制的频段频谱整形滤波器a(ω)的幅频响应计算其单位冲激响应。
步骤3,将白噪声σ(n)经过频谱整形滤波器a(ω)滤波得到频谱整形滤波信号a(n)。
步骤4,将频谱整形滤波信号a(n)经过控制滤波器w(ω)滤波,得到控制滤波信号b(n)。
步骤5,使用误差传感器所拾取的误差信号e(n)减去馈给次级声源的控制信号y(n)经次级路径建模滤波器
步骤6,通过公式
步骤7,不断迭代控制滤波器系数w(n),使得代价函数j=e[e2(n)]+e[b2(n)]最小,e[]表示求期望。
优选的:步骤6控制滤波器系数迭代公式的得到方法包括以下步骤:
步骤61,代价函数的频域形式定义为:
式中,pe(ω)为误差信号的功率谱密度,w’(ω)为控制滤波器系数的傅里叶变换,pa(ω)为信号a(n)的功率谱密度。
步骤62,将误差信号e(n)=p(n)+wt(n)r(n)代入代价函数的频域形式,得:
j=e[p2(n)]+2wtp+wt(r+a)w
式中,p(n)为初始噪声信号,r为滤波-x信号向量r(n)自相关矩阵,a为频谱整形滤波信号向量a(n)的自相关矩阵,p为初始噪声信号p(n)和滤波-x信号向量r(n)的互相关向量。
步骤63,代价函数j得瞬时梯度
步骤64,使用随机梯度下降法,得控制滤波器系数迭代公式。
优选的:初始噪声信号p(n)和滤波-x信号向量r(n)的互相关向量p:p=e[p(n)r(n)]。
优选的:滤波-x信号向量r(n)自相关矩阵r:r=e[r(n)rt(n)]。
优选的:频谱整形滤波信号向量a(n)的自相关矩阵a:a=e[a(n)at(n)]。
本发明相比现有技术,具有以下有益效果:
(1)本发明提出的方法与非自适应滤波器设计方法相比,可用于实时自适应系统。
(2)本发明与lfxlms算法相比,可在自适应反馈有源控制系统中实现对一个或多个特定频段的水床抑制,降噪效果更好。
(3)本发明与glfxlms算法相比,避免了迭代过程中矩阵与向量相乘的复杂操作,运算量大幅降低,更具有实用性。
附图说明
图1是本发明的算法框图。
图2是不同阶数的频谱整形滤波器幅频响应。
图3是本发明方法与传统fxlms算法,lfxlms算法和glfxlms算法降噪前后噪声信号功率谱密度对比图。
图4是本发明算法与传统fxlms算法,lfxlms算法和glfxlms算法稳态滤波器幅频响应对比图。
具体实施方式
下面结合附图和具体实施例,进一步阐明本发明,应理解这些实例仅用于说明本发明而不用于限制本发明的范围,在阅读了本发明之后,本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。
一种自适应反馈有源控制系统水床效应抑制的方法,如图1所示,通过以下技术方案来实现:
(1)测量有源控制系统次级路径传递函数单位冲激响应,得到次级路径函数的估计
(2)根据需要抑制水床效应的频段设计频谱整形滤波器a(ω)的幅频响应,在需要抑制的频段a(ω)幅值设计为较大,其他频段a(ω)幅值设计为相对较小,根据幅频响应计算其单位冲击响应。
(3)将白噪声σ(n)经过频谱整形滤波器a(ω)滤波得到信号a(n)。
(4)将信号a(n)经过控制滤波器w(ω)滤波,得到信号b(n)。
(5)使用误差传感器所拾取的误差信号e(n)减去馈给次级声源的控制信号y(n)经次级路径建模滤波器
(6)通过公式
(7)不断迭代控制滤波器系数w(n),使得代价函数j=e[e2(n)]+e[b2(n)]最小。
根据图1所示的本发明算法框图,其原理简介如下:
设定控制滤波器长度l,频谱整形滤波器长度la,次级路径单位冲击响应长度m,迭代步长μ及白噪声σ(n)的幅度。
本发明方法的代价函数的时域形式为:
j=e[e2(n)]+e[b2(n)](1)
式中b(n)=wt(n)a(n)称为惩罚信号。a(n)=[a(n),a(n-1),…,a(n-l+1)]t,a(n)为高斯白噪声σ(n)经过频谱整形滤波器a(ω)滤波后的信号,l为控制滤波器w(n)的阶数,e(n)为误差信号,符号e[]表示求期望。
根据维纳-辛钦定理,代价函数的频域形式定义为:
式中pe(ω)为误差信号的功率谱密度,w(ω)为控制滤波器系数的傅里叶变换,pa(ω)为信号a(n)的功率谱密度。式(2)表明,信号a(n)的功率谱密度pa(ω)为权重项,它使得代价函数对不同频段的控制滤波器幅值以不同的权重进行约束,降低该频段输出信号的大小,减少“水床”效应引起的噪声放大。
将误差信号e(n)=p(n)+wt(n)r(n)代入(1)式中,得:
j=e[p2(n)]+2wtp+wt(r+a)w(3)
式中r和a分别为滤波-x信号向量r(n)和a(n)的自相关矩阵,p为初始噪声信号p(n)和r(n)的互相关向量,分别定义如下:
p=e[p(n)r(n)](4)
r=e[r(n)rt(n)](5)
a=e[a(n)at(n)](6)
式中r(n)=[r(n),r(n-1),…,r(n-l+1)]t为滤波-x信号向量,
使用随机梯度下降法,得控制滤波器系数迭代公式为:
式中μ为迭代步长。因该算法可实现对特定频段控制滤波器约束,故称其为频段约束滤波-x最小均方(frequencybandconstrainedfiltered-xleastmeansquare)算法,简称fcfxlms算法。
下面以有源降噪头靠系统为例说明本发明的效果,有源降噪头靠系统一般布置在人耳附近,使用扬声器作为次级声源,通过降低人耳附近误差传声器的噪声,在人耳附近产生静区。每只耳朵使用一个控制通道,包含一个次级声源和一个误差传声器,误差传声器距离次级声源振膜中心8cm。2只耳朵共2个通道,一般而言,有源降噪头靠系统的2个通道耦合较弱,每一通道可视为单通道系统。由于头靠系统使用场合限制,扬声器尺寸不能太大,如集成于汽车、飞机座位的扬声器,其低频响应有限,例如本实施例中作为次级声源的扬声器在小于100hz的低频无法产生足够大的声压,若次级源在小于100hz的低频输出较大,有可能导致次级源输出信号失真,额外产生噪声,甚至损坏扬声器,因此有必要对该频段的滤波器幅值进行约束。另一方面,人耳对某些中高频段的信号相对更为敏感,不希望该频段的噪声被放大。因此故将频谱整形滤波器a(ω)设置为一个低通滤波器与一个带通滤波器组合的形式。其中低通滤波器的通带截止频率为150hz,阻带截止频率为200hz,通带幅值和阻带幅值分别为0.01和0.0018。带通滤波器的通带上、下截止频率分别为1000hz和2000hz,过渡带宽为100hz,通带幅值和阻带幅值分别为0.01和0.0018。根据幅频响应计算其单位冲激响应。设计了频谱整形滤波器a(ω),可使用上述本发明技术方案(1)~(7)来实现本发明,其中方案中的第(2)项即将频谱整形滤波器a(ω设置为此处描述的低通滤波器与带通滤波器组合。
为了说明本发明方法的优点,以下利用仿真对传统的lfxlms算法、glfxlms算法和本发明提出的fcfxlms算法的稳态性能进行比较验证。使用上述有源降噪头靠系统实测的传递函数进行仿真,使用一个音箱作为初级声源,初级噪声为方差为10-10的白噪声经过一个传递函数为h(z)=[(1-2z-2+z-4)/(1-3.91z-1+5.76z-2-3.79z-3+0.94z-4)]的带通滤波器滤波后的信号。自适应控制滤波器长度l=512,频谱整形滤波器长度la=512,迭代步长μ=0.1,白噪声为满足标准正态分布的白噪声,采样率为16khz。使用四种不同长度的频谱整形滤波器的拟合效果如图2所示,图中红色实线为理想频响,使用长度为512的频谱整形滤波器可较好地拟合理想频响。使用上述各算法获得的降噪量,1000-2000hz频段噪声放大平均值,控制滤波器100hz以下幅度峰值及迭代公式计算量如表1所示。表1中fcfxlms算法迭代公式的计算量包含了(8)式中a(n)和b(n)的计算。使用不同算法控制前后噪声信号的功率谱密度如图3所示,图中primary代表降噪前噪声信号,虚线框内频段为目标约束频段。使用不同算法收敛后控制滤波器系数幅频响应如图4所示。
表1不同算法降噪性能和计算量对比
图3和表1显示:使用fxlms算法可获得最大降噪量(18.6db),但其在1000-2000hz噪声放大量较大,同时控制滤波器在100hz以下幅值较大,其峰值为-1.9db。使用lfxlms可有效降低由水床效应引起的噪声放大,同时较好地抑制100hz以下控制滤波器幅值,但会牺牲降噪量(仅有10.6db)。使用glfxlms和本发明提出的fcfxlms获得效果类似,降噪量为13.1db,控制滤波器100hz以下幅度峰值为-16.0db,相对于lfxlms,以牺牲部分降噪量降低了1000-2000hz的噪声放大。但fcfxlms的计算量远小于glfxlms,当滤波器阶数为512频谱整型滤波器的数la为512时,前者乘法与加法共为4096次,后者为33792次,总计算量降低约8倍。
使用以上几种算法,得到的收敛后的控制滤波器w(n)的幅频响应如图4所示。本发明所提的fcfxlms算法和传统的glfxlms算法可实现对控制滤波器不同频段的加权约束,权重项可自由设计。本例中,在100hz以下和1000-2000hz频段设置了较大权重以抑制该频段内控制滤波器的幅值,在其他频段使用相对较小权重以减小降噪量的下降。fcfxlms算法和glfxlms算法收敛后的控制滤波器基本完全重合,如图4中实线和方形标记线所示。
以上所述仅是本发明的优选实施方式,应当指出:对于本技术领域的普通技术人员来说,在不脱离本发明原理的前提下,还可以做出若干改进和润饰,这些改进和润饰也应视为本发明的保护范围。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



