一种基于四元数自适应滤波器的滤波-X最小均方有源噪声控制方法与流程

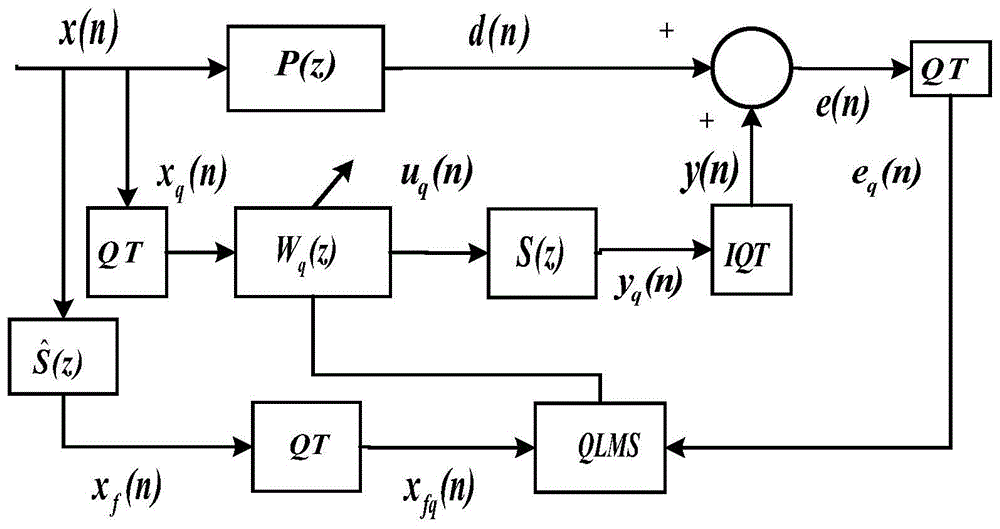
本发明涉及有源噪声控制领域，尤其涉及一种基于四元数自适应滤波器的滤波-x最小均方有源噪声控制方法。

背景技术：

噪声污染是一个全世界都十分关注的环境问题，随着现代工业、交通运输业的发展、噪声污染日益严重，如何有效地减少或控制噪声是迫切需要解决的问题。传统的噪声控制采用无源控制方式，对中、高频噪声具有较好的控制效果，但无法有效消除低频噪声，或需要付出较重的重量代价。针对传统噪声控制方法的不足，有源噪声控制提供了一种对低频噪声行之有效的控制方法。

anc系统的性能取决于收敛时间、稳态性能。随着数字信号处理理论和技术的逐步成熟，基于自适应滤波理论的有源噪声控制技术开始发展，滤波-x最小均方算法(fxlms)被提出并被广泛应用，然而该算法的瞬态特性及稳态特性都有改进的空间。fxlms算法使用的是lms算法来更新控制滤波器的权值，由于输入信号的自相关矩阵的特征值分散的问题会导致lms算法慢的收敛模式。并且考虑到现代环境声音的多维度传播，因此，将lms算法引入到复数域，其中具有代表性的是四元数自适应滤波器(qlms)。四元数最小均方(qlms)算法通过直接在数据所在的多维域中进行处理并采用这些维之间的关联和耦合来提供密集的建模。在anc系统模型中需要预先知道次级通道的传递函数，但通常情况下它是未知的，次级通道(从噪声控制滤波器的输出到误差传感器测量残余噪声的路径)的存在也会导致滤波器的不稳定性，因此为了确保anc系统的收敛，需要对次级通道路径进行建模，以跟踪次级路径的变化，从而提高anc系统降噪性能的稳定性。常用的建模方法包括离线建模和在线建模，本文将采取离线建模中的附加随机噪声法对次级通道进行建模。

发明目的

本发明的目的在于应对现有技术的不足，提供一种基于四元数自适应滤波器的滤波-x最小均方有源噪声控制方法，具体为基于四元数的自适应滤波器结构，对控制滤波器采用四元数lms算法对控制滤波器的权值进行更新，采用超平面的四元数，实现多维滤波，从而能够充分保持多维信号所具有的内部关系，从而使得处理精度具有优越性，提高了算法的收敛性能，改善了降噪性能。在此基础上，将一维的lms算法扩展到具有多维的qlms算法当中，实现四维空间的误差优化，突破了一维信号的限制，使其性能更加优越和稳定。本发明在可以保证良好降噪性能的基础上，减少整个anc系统的收敛时间，从而提高收敛速度。

技术实现要素：

本发明提出了一种基于四元数自适应滤波器的滤波-x最小均方有源噪声控制方法，通过设计一个有源噪声控制anc系统进行降噪，包括以下步骤：

步骤一、产生白噪声并将其用扬声器输出，再通过拾音器采集，然后利用最小均方准则，通过建立次级通道的模型，进行多次迭代后得到次级通道系数；

步骤二、通过利用扬声器产生反噪声来抵消外界噪声，具体为通过拾音器采集外界噪声信号，利用步骤一中得到的次级通道系数进行补偿，即，根据fxqlms算法计算反噪声，并通过扬声器发出从而抵消外界噪声，该过程进行多次迭代从而实现降噪；

所述建立次级通道的模型采用附加随机噪声的方法，假定次级通道为时不变系统，采用白噪声发生器产生一个随机噪声并输入建模滤波器和次级通道作为参考信号，将误差传感器测得的信号当作建模滤波器的目标信号，其中，所述白噪声发生器产生高斯白噪声，并注入次级通道模型的次级路径；

所述anc系统包括主通道路径函数p(z)、次级通道路径传递函数s(z)、次级通道路径估计函数滤波器wq(z)，其中，输入噪声信号x(n)分别输入至主通道路径函数p(z)、控制滤波器wq(z)和次级通道路径估计函数

x(n)通过主通道路径，经由主通道路径函数p(z)进行滤波，得到主通道待降噪点处的预期噪声信号d(n)；

输入噪声信号x(n)经过qt模块，由一维信号变为四维信号xq(n)，表示为如式(1)所示：

xq(n)＝0+x(n)i+x(n)j+x(n)k(1)；

控制滤波器wq(z)分别与噪声源信号xq(n)和fxqlms算法模块相连接，噪声源信号xq(n)再通过控制滤波器wq(z)输出信号uq(n)，信号uq(n)再经过次级通道路径传递函数s(z)产生抗噪信号yq(n)，抗噪信号yq(n)经过iqt模块，由四维信号变为了一维信号y(n)，即取抗噪信号yq(n)的第一个虚部，即i的系数组成y(n)，y(n)表示主动降噪输出的降噪信号，y(n)与d(n)相抵消的进行结合，从而减少了误差传感器周围的声压，用信号e(n)代表y(n)与d(n)之间的误差信号，即d(n)-y(n)；一维信号e(n)经过qt模块变为四维的误差信号eq(n)，该误差信号eq(n)输入至fxqlms算法模块；

输入噪声信号x(n)通过次级通道路径估计函数输出滤波-x信号xf(n)，xf(n)经过qt模块变为四维的滤波-x信号xfq(n)，xfq(n)被输入至fxqlms算法模块，fxqlms算法模块连接至控制滤波器wq(z)，用于更新权值。

所述建立次级通道的模型的方法包括以下步骤：

1)由白噪声发生器发出白噪声信号u(n)，驱动次级扬声器，同时作为自适应滤波器和lms算法的参考输入信号，该作为anc系统的次级通道路径估计函数；

2)利用传声器采集次级扬声器的输出信号y(n)；

3)计算自适应滤波器的输出信号如式(2)所示：

其中m是滤波器长度；

4)计算实际系统和辨识系统的输出差值，如式(3)所示：

5)采用lms算法更新自适应滤波器的系数，如式(4)所示：

si(n+1)＝si(n)+μe(n)u(n-i)(4)，

其中，i＝0,1,…m-1；

6)重复上述过程，直到误差信号e(n)满足设定的要求为止，存储的系数，供fxqlms算法模块使用。

优选地，使用参考传感器及误差传感器分别采集参考输入信号xq(n)及误差信

号eq(n)，计算滤波器的输出信号uq(n)，如式(5)所示：

其中，m是滤波器长度，输出信号uq(n)以驱动次级扬声器；

计算滤波-x信号xf(n)，如式(6)所示：

其中，si(n)是n时刻次路径估计的第i个脉冲响应系数；

采用fxqlms算法更新四元数自适应控制滤波器wq(z)的权值系数，如式(7)所示：

wq(n+1)＝wq(n)+μ(2eq(n)xfq^*(n)-xfq^*(n)eq^*(n))(7)，

重复上述过程，直到误差信号eq(n)满足设定的要求为止。

优选地，在误差麦克风处，即误差信号eq(n)输出处，监测其降噪性能，根据式(8)-(10)评估降噪性能和收敛速度：

ae(n)＝λae(n-1)+(1-λ)|e(n)|；(9)

ad(n)＝λad(n-1)+(1-λ)|d(n)|(10)；

其中anr(n)代表anc系统的降噪性能的好坏，ae(0)＝0,ad(0)＝0；λ是遗忘因子，λ＝0.999；e(n)代表anc系统控制滤波器wq(z)的误差函数；d(n)代表anc系统控制滤波器wq(z)的期望信号。

附图说明

图1为基于四元数自适应滤波器的有源控制噪声算法框图；

图2为次级通路的建模框图；

图3为fxlms和fxqlms两种算法的权重更新曲线对比图；

图4、图5为anc系统综合仿真结果图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、详细地描述。所描述的实施例仅仅是本发明的一部分实施例。

本发明解决上述技术问题的技术方案是：

如附图1所示，给出了基于四元数自适应滤波器的有源噪声控制框图。本发明提出一种基于fxqlms算法的主动噪声控制(anc)系统的设计，能够降低lms算法由于参考信号的自相关矩阵的特征值分散程度的敏感性使得控制滤波器的收敛时间大大降低，使得整个anc系统的收敛时间大大降低，其特征在于，用于对参考输入信号采用fxqlms算法，更新控制滤波器wq(z)的权系数，控制滤波器wq(z)分别与噪声源和fxqlms算法模块相连接，原始的噪声信号通过控制滤波器wq(z)输出uq(n)，uq(n)再经过次级通道产生抗噪信号yq(n)，取其虚部i的系数得到抗噪信号y(n)与主路径的噪声d(n)相结合以减少误差传感器周围的声压；主通道路径p(z)，用于(模拟anc系统主通道的路径函数(声学响应)从而对初始信号进行滤波，得到主通道自适应滤波器的期望信号d(n))。

次级路径对于滤波器降噪性能影响很大，因此，需要首先辨识次路径的模型。次级通路的建模可以采用在线建模和离线建模，次级通道在线建模的方法包括期望信号抵消法和附加随机噪声法。次级通道离线建模有三种方法可以选择：时延预估法、采用两个传声器的方法以及附加随机噪声法。在线建模一般用在次级通道的模型不断随着时间变化的情况下，即次级通道的建模算法和anc系统的fxlms算法要一起运行，次级通道的建模算法可以随着模型运行过程中系统的变化来不断改变模型中的滤波器权值；而离线建模方法是在anc系统算法运行前就已经得到了次级通道的传递函数，然后再将已有的传递函数用于主动控制系统中，这种方法经常用在次级通道的模型比较稳定的情况下。假设次级通道为时不变系统，将选用离线建模中附加随机噪声的方法对次级通道进行建模。这种方法是在anc系统建模之前单独进行的，采用噪声发生器产生一个随机噪声并输入建模滤波器和次级通道作为参考信号，误差传感器测得的信号当作建模滤波器的目标信号。

随机噪声法对次路径进行建模原理如图2所示，图2示出了次路径建模框图。假设次级通道为时不变系统，将选用离线建模中附加随机噪声的方法对次级通道进行建模。这种方法是在anc系统建模之前单独进行的，采用噪声发生器产生一个随机噪声并输入建模滤波器和次级通道作为参考信号，误差传感器测得的信号当作建模滤波器的目标信号。可得出次级通路的传递函数。在本发明中，需要预先辨识次路径的模型采用白噪声信号作为激励信号的目的是充分激励次路径的各个频率成分。具体而言，白噪声强度为0.01，建模确定的次通道估计传递函数估计如下：

设置主通路的传递函数为

p(z)＝0.1+0.25z^-1+0.5z^-2+z^-3+0.5z-⁴+0.25z^-5+0.1z^-6

次级通路的传递函数为

s(z)＝0.025+0.0625z^-1+0.125z^-2+0.0625z^-3+0.025z^-4

本发明中，滤波器长度m＝32，输入参考信号定义为其中v(n)是方差为0.1的零平均白高斯噪声。

一维信号向四元数转换(quaterniontransform,qt)的具体实现方法为：

xq(n)＝qt[x(n)]＝0+x(n)i+x(n)j+x(n)k；

xfq(n)＝qt[xf(n)]＝0+xf(n)i+xf(n)j+xf(n)k；

相应地，四元数反转换回常规一维信号(inversequaterniontransform,iqt)的具体实现方法为：

y(n)＝iqt[yq(n)]＝x(yq(n))，x(yq(n))代表取值为四元数yq(n)的虚部i的系数。

如附图3所示，给出了fxlms和fxqlms两种算法的权重更新曲线对比图。从图中可以看出，fxlms的权重更新曲线在循环迭代次数达到40000次左右才趋于稳定，fxqlms的权重更新曲线在循环迭代次数达到15000次左右就已经趋于稳定，最终都趋向稳定于2.13附近。

附图4展示了算法的anr的学习曲线。图中，两根曲线分别表示滤波器长度m＝32，遗忘因子μ＝0.00001时fxlms算法的anr曲线以及fxqlms算法的anr曲线。从图中可以看出随着anc系统迭代次数的不断增加，对初始参考噪声信号的降噪效果也在不断的提高，降噪效果明显，收敛速度也有一定的提高。具体来讲，fxlms算法的anr曲线当迭代次数达到25000时，fxqlms算法的anr曲线当迭代次数达到10000时，趋于稳定，可见fxqlms算法收敛效果明显较好。

附图5展示了以e(e(k)²)计算的两种算法的均方误差mse的学习曲线，图中，两根曲线分别表示滤波器长度m＝32，遗忘因子μ＝0.00001时fxlms算法的mse曲线以及fxqlms算法的mse曲线。从图中能够看出随着anc系统迭代次数的不断增加,fxlms算法的anr曲线当迭代次数达到25000时，fxqlms算法的anr曲线当迭代次数达到10000时，趋于稳定。可见fxqlms算法反映了anc系统的降噪性能和收敛速度均有改善。

总而言之，由于噪声的传播是沿着不同方向进行的，采用四元数可以模拟声音传播的多向性，从而加符合声音传播的实际情况。又由于实时降噪最重要的问题就是收敛性，本发明采用四元数最小均方算法qlms来实现，可以在四维空间中进行优化，使得优化结构更加合理，能够以更快的速度收敛。

本发明具有如下有益效果：

1.结构简单，采用基本降噪结构为fxlms。

2.由仿真结果显示，降噪性能和收敛速度有明显的提高。

3.从一维信号扩展到多维信号，更加符合噪声传播的实际情况。

本领域技术人员应该理解，本发明的实施例仅用于示例性的阐述本发明，而不应该视为对本发明保护范围的限制，任何不脱离本发明主旨和思想的变体、修改均落入本发明的保护范围，本发明的保护范围由所提交的权利要求书限定。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除