秘密批量近似系统、秘密计算装置、秘密批量近似方法、以及程序与流程

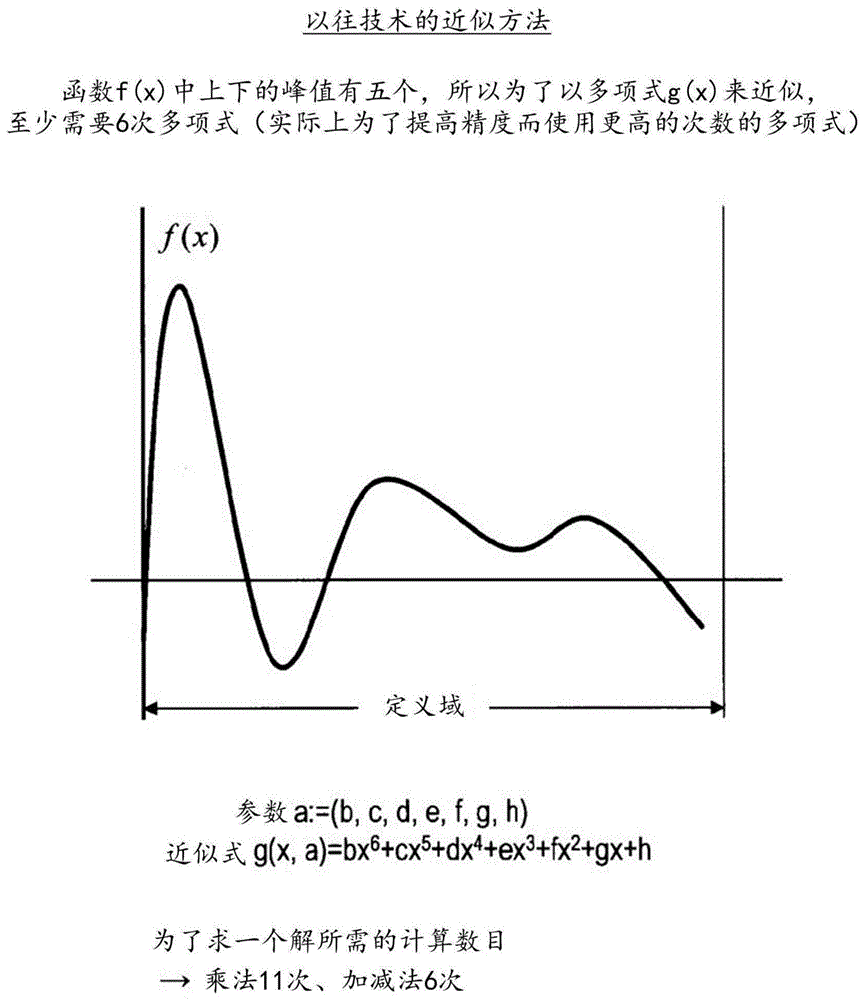
本发明涉及通过秘密计算进行函数的近似计算的技术。

背景技术：

作为在不对加密后的数值进行复原的情况下得到特定的运算结果的方法，有被称为秘密计算的方法(例如，参考非专利文献1)。在非专利文献1中记载的方法中，进行使数值的片段分散到三个秘密计算装置这样的加密，三个秘密计算装置进行协调计算，从而能够在不对数值进行复原的情况下使加减法、常数加法、乘法、常数倍、逻辑运算(非、逻辑与、逻辑或、异或)、数据形式变换(整数、二进制)的结果以被分散到三个秘密计算装置的状态、即被加密的状态来保持。

作为在秘密计算上实现指数函数或对数函数等复杂的函数的计算的方法，近似于能够通过加减法和乘法的组合来计算的多项式而进行计算。例如，在非专利文献2中记载有将指数函数近似于多项式来计算的方法。

现有技术文献

非专利文献

非专利文献1：千田浩司、濱田浩気、五十嵐大、高橋克巳、“軽量検証可能3パーティ秘匿関数計算の再考”、css、2010年

非专利文献2：liinakammandjanwillemson，"securefloatingpointarithmeticandprivatesatellitecollisionanalysis，"internationaljournalofinformationsecurity，vol.14，no.6，pp.531-548，2015.

技术实现要素：

发明要解决的课题

但是，在以往技术中，在以多项式来近似复杂的函数的情况下，为了提高近似的精度而需要提高多项式的次数。例如，在非专利文献2中为了实现指数函数的计算而计算了基于4次多项式的近似式。此外，就在逻辑回归或神经网络中使用的sigmoid函数而言，为了得到充分的精度而至少需要10次多项式。若多项式的次数n提高则在o(n)中加减法或乘法的次数增加，所以计算时间增大。

本发明的目的在于，鉴于上述那样的技术课题，在以秘密计算来计算复杂的函数时减少计算时间而不降低近似的精度。

用于解决课题的手段

为了解决上述的课题，本发明的一方式的秘密批量近似系统包括多个秘密计算装置，所述秘密批量近似系统将n个值x:＝(x1，……，xn)的隐匿文[x]:＝([x1]，……，[xn])作为输入，将m设为2以上的整数，将i设为1以上且m以下的各整数，计算作为yj＝f(xj)的函数值y:＝(y1，……，yn)的近似值z:＝(z1，……，zn)的隐匿文[z]:＝([z1]，……，[zn])，其中，将g设为对在将函数f分割为m个区间时的各区间进行近似的多项式，将ri设为区间，将pi设为与区间ri对应的多项式g的参数，秘密计算装置包括：参数取得单元，针对1以上且n以下的各整数j，将aj设为与包含值xj的区间ri对应的参数pi，取得与值x:＝(x1，......，xn)对应的参数a:＝(a1，......，an)的隐匿文[a]:＝([a1]，……，[an])；以及多项式计算单元，使用参数a的隐匿文[a]计算将值x的隐匿文[x]作为输入的多项式g([x]，[a])，得到函数值y的近似值z的隐匿文[z]。

发明效果

根据本发明的秘密批量近似技术，在以秘密计算来计算复杂的函数时，能够以比以往更低的次数的多项式来近似，所以能够减少计算时间而不降低近似的精度。

附图说明

图1是用于说明以往技术的近似方法的图。

图2是用于说明以往技术的处理的流程的图。

图3是用于说明本发明的近似方法的图。

图4是用于说明本发明的处理的流程的图。

图5是例示秘密批量近似系统的功能结构的图。

图6是例示秘密计算装置的功能结构的图。

图7是例示秘密批量近似方法的处理动作过程的图。

具体实施方式

首先，针对本说明书中的记载方法以及术语的定义进行说明。

<记载方法>

将通过加密或秘密分散等将某值a隐匿化后的值称为a的隐匿文，记载为[a]。此外，将a称为[a]的明文。在隐匿化为秘密分散的情况下，通过[a]来参照各秘密计算装置所具有的秘密分散的片段的集合。

变量的定义域中的[a，b](方括号)表示闭区间，(a，b)(圆括号)表示开区间。例如，i∈[a，b]表示i取a以上且b以下的值。此外，i∈[a，b)表示i取a以上且小于b的值。

＜加法、减法、乘法＞

在对于隐匿文的加法、减法、乘法的各运算中，将两个值a、b的隐匿文[a]、[b]作为输入，分别计算a+b、a-b、ab的计算结果c1、c2、c3的隐匿文[c1]、[c2]、[c3]。将这些运算的执行分别如下式那样进行描述。

[数式1]

[c1]←add([a],[b]),

[c2]←sub([a],[b]),

[c3]←mul([a],[b])

在没有招致误解的顾虑的情况下，将add([a]，[b])、sub([a]，[b])、mul([a]，[b])分别略记为[a]+[b]、[a]-[b]、[a]×[b]。

<批量映射(batchmapping)>

批量映射的运算中，将n个值(x1，……，xn)(其中，设为各xj关于后述的um满足xj<um)的隐匿文([x1]，……，[xn])以及m个值(u1，……，um)(其中ui<ui+1)和m个值(a1，……，am)的组作为输入，计算n个值(y1，……，yn)(其中，将j设为满足uj≤xi<uj+1的值。设为各yi满足yi＝aj)的隐匿文([y1]，……，[yn])。将该运算的执行如下式那样进行描述。

[数式2]

([y1],…,[yn])←batchmap(([x1],…,[xn]),(u1,…,um),(a1,…,am))

通过秘密计算高效地计算批量映射的秘密计算批量映射算法在下述参考文献1以及2中被记载。

参考文献1：濱田浩気,五十嵐大,千田浩司,“秘匿計算上の一括写像アルゴリズム”,電子情報通信学会論文誌a,vol.j96-a,no.4,pp.157-165,2013参考文献2：peeterlaud，"parallelobliviousarrayaccessforsecuremultipartycomputationandprivacy-preservingminimumspanningtrees"，popets2015(2)，pp.188-205，2015.

发明内容

在本发明中，利用以下情况：即使是复杂的函数，只要限定区间，以低次的多项式就能够以充分的精度来近似。具体而言，将函数分割为多个区间，将各区间以次数更低的多项式来近似，从而将函数整体以多个低次的多项式来近似。在实际计算时，确定输入被包含于哪个区间，使用与该区间相应的参数来计算低次的多项式。由此，在以批量的方式进行多个计算的情况下，能够以更低的次数的近似式实现与以往同等精度的近似。多项式的计算时间与次数成比例，所以作为整体能够削减计算时间而不降低近似的精度。

在图1中示出通过以往技术以多项式近似来计算复杂的函数的具体例。就计算对象的函数f(x)而言，上下的峰值(peak)有五个，所以为了以多项式g(x，a)来近似，至少需要6次多项式。实际上为了得到充分的精度，以更高的次数的多项式来近似。例如，多项式g(x，a)的参数a为a:＝(b，c，d，e，f，g，h)，多项式g(x，a)能够定义为g(x，a)＝bx⁶+cx⁵+dx⁴+ex³+fx²+gx+h。在该情况下，为了求一个解所需的计算数目成为乘法11次、加减法6次。

在图2中示出以往技术的处理的流程。首先，计算对函数f(x)进行近似的多项式g(x，a)的参数a。接着，使用输入值x:＝(x1，……，xn)的隐匿文[x]:＝([x1]，……，[xn])和参数a，针对1以上且n以下的各整数j计算多项式[zj]＝g([xj]，a)，得到函数值y:＝(y1，……，yn)的近似值z:＝(z1，……，zn)的隐匿文[z]:＝([z1]，……，[zn])。

在图3中示出通过本发明以多项式近似的方式计算复杂的函数的具体例。将计算对象的函数f(x)的定义域分割为m个区间，将各区间以2次多项式(即2次函数)来近似。此时，多项式g(x，a)的参数a为a:＝(b，c，d)，多项式g(x，a)能够定义为g(x，a)＝bx²+cx+d。在该情况下，为了求一个解所需的计算数目能够减少为乘法3次、加减法2次。

在图4中示出本发明的处理的流程。首先，计算对函数f(x)的各区间ri(i＝1，……，m)进行近似的多项式g(x，a)的参数pi。接着，使用输入值x:＝(x1，……，xn)的隐匿文[x]:＝([x1]，……，[xn])以及区间(r1，……，rm)和参数(p1，……，pm)的组来计算n个参数的隐匿文[a]:＝([a1]，……，[an])。在此，[aj]是与xj所属的区间ri对应的参数pi的隐匿文。最后，使用输入值x:＝(x1，……，xn)的隐匿文[x]:＝([x1]，……，[xn])和参数a:＝(a1，……，an)的隐匿文[a]:＝([a1]，……，[an])，针对1以上且n以下的各整数j计算多项式[zj]＝g([xj]，[aj])，得到函数值y:＝(y1，……，yn)的近似值z:＝(z1，……，zn)的隐匿文[z]:＝([z1]，……，[zn])。

以下，针对本发明的实施方式详细地进行说明。另外，对在附图中具有相同的功能的结构单元赋予相同的序号，省略重复说明。

[第一实施方式]

参考图5，说明第一实施方式的秘密批量近似系统100的结构例。秘密批量近似系统100包括k(≥2)台秘密计算装置11，……，1k。在本方式中，秘密计算装置11，……，1k分别被连接到通信网9。通信网9是被构成为所连接的各装置能够相互进行通信的线路交换方式或分组交换方式的通信网，例如能够使用互联网或lan(局域网(localareanetwork))、wan(广域网(wideareanetwork))等。另外，各装置不一定能够经由通信网9以在线的方式进行通信。例如，也可以构成为将要输入至秘密计算装置11，……，1k的信息存储至磁带或usb存储器等可移动型记录介质，从该可移动型记录介质向秘密计算装置11，……，1k以离线的方式输入。

参考图6，说明本方式的秘密批量近似系统100中包含的秘密计算装置1k(k＝1，……，k)的结构例。秘密计算装置1k例如如图6所示，包括存储单元10、输入单元11、参数取得单元12、多项式计算单元13、以及输出单元14。该秘密计算装置1k(k＝1，……，k)一边与其他秘密计算装置1k'(k'＝1，……，k，其中k≠k')协调一边进行后述的各步骤的处理，从而本方式的秘密批量近似方法被实现。

秘密计算装置1k例如是在具有中央运算处理装置(中央处理单元(cpu:centralprocessingunit))、主存储装置(随机存取存储器(ram:randomaccessmemory))等的公知或者专用的计算机中读入特殊的程序而构成的特殊的装置。秘密计算装置1k例如在中央运算处理装置的控制下执行各处理。被输入至秘密计算装置1k的数据或在各处理中得到的数据例如被储存至主存储装置，在主存储装置中储存的数据根据需要被读出至中央运算处理装置而被利用于其他处理。就秘密计算装置1k的各处理单元而言，也可以是至少一部分由集成电路等硬件构成。秘密计算装置1k所具备的各存储单元例如能够由以下结构构成：ram(随机存取存储器(randomaccessmemory))等主存储装置、由硬盘或光盘或闪速存储器(flashmemory)那样的半导体存储器元件构成的辅助存储装置、或者关系数据库或关键字储存器(key-valuestore)等中间件。

参考图7，说明本方式的秘密批量近似系统100所执行的秘密批量近似方法的处理动作过程。

在各秘密计算装置1k的存储单元10中，存储有多项式g(x，a)以及区间和参数的组的列(sequence)((r1，p1)，……，(rm，pm))。多项式g(x，a)是对在将计算对象的函数f(x)分割为特定的m个区间时的各区间进行近似的多项式，是比对函数f(x)整体进行近似时的多项式更低次的多项式。a是对多项式g(x，a)进行定义的参数，例如是对各项的系数进行排列后的排列(array)。ri(i＝1，......，m)是表示在将函数f(x)分割为m个区间时的各区间的信息。pi(i＝1，……，m)是在将函数f(x)的区间ri以多项式g(x，a)来近似时的参数。

在步骤s1中，各秘密计算装置1k的输入单元11获取作为计算对象的n个值x:＝(x1，……，xn)的隐匿文[x]:＝([x1]，……，[xn])作为输入。输入单元11将值x的隐匿文[x]输出至参数取得单元12。

在步骤s2中，各秘密计算装置1k的参数取得单元12从输入单元11获取值x的隐匿文[x]，针对1以上且n以下的各整数j，从在存储单元10中存储的区间和参数的组的列((r1，p1)，……，(rm，pm))取得满足s.t.aj＝pi，xj∈ri的n个参数a:＝(a1，……，an)的隐匿文[a]:＝([a1]，……，[an])。即，针对1以上且n以下的各整数j，将aj设为与值xj对应的区间ri的参数pi，生成与值x1，......，xn分别对应的参数a1，......，an的隐匿文[a1]，……，[an]。参数取得单元12将值x的隐匿文[x]和参数a的隐匿文[a]输出至多项式计算单元13。

在步骤s3中，各秘密计算装置1k的多项式计算单元13从参数取得单元12获取值x的隐匿文[x]和参数a的隐匿文[a]，针对1以上且n以下的各整数j，按照在存储单元10中存储的多项式g(x，a)，计算[zj]＝g([xj]，[aj])。多项式计算单元13将函数值y:＝(y1，……，yn)的近似值z:＝(z1，……，zn)的隐匿文[z]:＝([z1]，......，[zn])输出至输出单元14。

在步骤s4中，各秘密计算装置1k的输出单元14从多项式计算单元13获取函数值y的近似值z的隐匿文[z]，作为秘密计算装置1k的输出。

[第二实施方式]

在第二实施方式中，更具体而言，示出将定义域为x:＝[0，1000)的下式的sigmoid函数以2次函数来近似的情况的例。

[数式3]

在以下，以与第一实施方式的差异点为中心进行说明。

在各秘密计算装置1k的存储单元10中，存储有多项式g(x，a)以及区间和参数的组的列((r1，p1)，……，(rm，pm))。就本方式的多项式g(x，a)而言，将a:＝(b，c，d)设为参数，被定义为g(x，a)＝bx²+cx+d。本方式的区间ri被定义为ri:＝[li，ui)，i∈[1，m](其中，设为l1＝0，um＝1000，ui＝li+1，li≤ui，i∈[1，m))。本方式的参数pi被定义为pi:＝(bi，ci，di)。

本方式的各秘密计算装置1k的参数取得单元12将隐匿文[x]和(u1，......，um)，((b1，c1，d1)，......，(bm，cm，dm))作为输入，如下式那样执行秘密计算批量映射算法，从而取得参数a:＝(a1，......，an)的隐匿文[a]:＝([a1]，……，[an])。

[数式4]

([a1],…,[an])←batchmap([x],(u1,…,um),((b1,c1,d1),…,(bm,cm,dm)))

在此，aj针对满足xj∈ri的某i，满足aj＝(bi，ci，di)。

本方式的各秘密计算装置1k的多项式计算单元13针对1以上且n以下的各整数j，设为[aj]:＝([b'j]，[c'j]，[d'j])，通过计算下式，得到近似值zj的隐匿文[zj]。

[数式5]

[zj]←[b′i]×[xj]×[xj]+[c′i]×[xj]+[d′i]

本发明利用以下情况：即使是复杂的函数，只要限定区间，以低次的多项式就能够以充分的精度来近似。具体而言，预先将函数分割为特定数目的区间，求得用于将各区间以低次的多项式来近似的参数，根据输入值被包含于哪个区间而取得与该输入值对应的参数，从而进行基于低次的多项式的近似。由此，在以批量的方式进行多个计算的情况下，能够以更低的次数的多项式来实现与以往同等精度的近似。特别是，对多个输入值使用秘密计算批量映射算法来取得与各输入值对应的参数，从而能够更高效地进行多项式近似。例如，在逻辑回归的学习的各迭代计算中被大量需要的sigmoid函数中，为了在逻辑回归中得到充分的精度，有实验上至少需要10次的报告(参考参考文献3)，例如若将区间数设为5000则能够以3次的多项式实现相当于翻倍精度的精度下的近似，能够将实数的乘法和加法的次数削减为3成。

参考文献3：paymanmohasselandyupengzhang，"secureml:asystemforscalableprivacy-preservingmachinelearning，"in2017ieeesymposiumonsecurityandprivacy，sp2017，sanjose，ca，usa，may22-26，2017，pp.19-38.ieeecomputersociety，2017.

以上，针对本发明的实施方式进行了说明，但具体的结构并非限于这些实施方式，更不用说即使在不脱离本发明的宗旨的范围中有适宜设计的变更等，也被包含于本发明。实施方式中说明的各种处理不仅按照记载的顺序以时间序列来执行，也可以根据执行处理的装置的处理能力或者根据需要而并行或者单独地执行。

[程序、记录介质]

在由计算机实现在上述实施方式中说明的各装置中的各种处理功能的情况下，各装置应具有的功能的处理内容通过程序被描述。并且，通过由计算机执行该程序，从而上述各装置中的各种处理功能在计算机上被实现。

描述了该处理内容的程序能够记录至计算机可读取的记录介质。作为计算机可读取的记录介质，例如也可以是磁记录装置、光盘、光磁记录介质、半导体存储器等任意记录介质。

此外，该程序的流通例如通过对记录了该程序的dvd、cd-rom等可移动型记录介质进行销售、转让、借出等来进行。进而，也可以设为将该程序储存至服务器计算机的存储装置，经由网络，从服务器计算机向其他计算机转发该程序，从而使该程序流通的结构。

执行这样的程序的计算机例如首先将在可移动型记录介质中记录的程序或从服务器计算机转发的程序暂时储存至自身的存储装置。并且，在执行处理时，该计算机读取在自身的存储装置中储存的程序，执行按照所读取到的程序的处理。此外，作为该程序的别的执行方式，也可以设为计算机从可移动型记录介质直接读取程序，执行按照该程序的处理，进而，也可以在从服务器计算机向该计算机转发程序时，依次执行按照所获取到的程序的处理。此外，也可以设为不进行从服务器计算机向该计算机的程序的转发，通过仅通过该执行指示和结果取得来实现处理功能的所谓asp(应用服务提供商(applicationserviceprovider))型的服务，执行上述的处理的结构。另外，设为在本方式中的程序中，包含供于基于电子计算机的处理用的信息并且是遵循程序的信息(并非对于计算机的直接的指令，但其是具有对计算机的处理进行规定的性质的数据等)。

此外，在该方式中，设为通过使得在计算机上执行特定的程序，构成本装置，但也可以以硬件的方式实现这些处理内容的至少一部分。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除