一种基于深度强化学习的空间双臂系统约束运动规划方法与流程

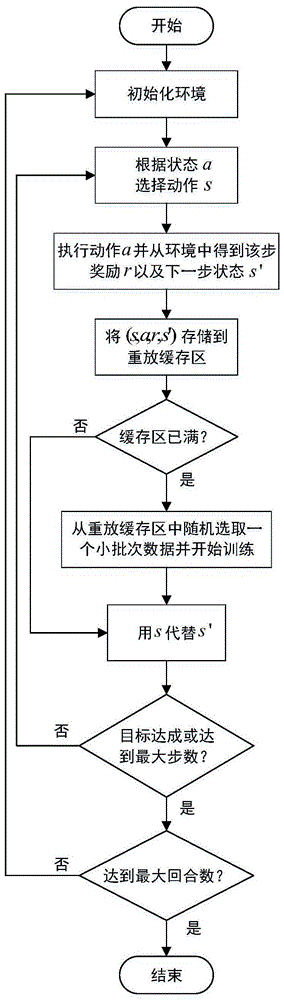
本发明属于空间机械臂运动规划技术领域，具体涉及一种基于深度强化学习的空间双臂系统约束运动规划方法。

背景技术：

空间机械臂作为空间操控任务中十分有效的一种执行机构，在修复故障卫星、清除空间碎片、组装大型空间结构等空间操控任务中都具有很高的工程应用价值。由于空间中微重力环境的影响，空间机械臂的运动特性与地面机械臂存在明显的差异，具体体现在地面机械臂一般具有固定的基座，而空间机械臂在执行任务的过程中基座一般都处于自由漂浮的状态。空间双机械臂系统相比于空间单机械臂系统而言在执行操控任务时更加安全可靠，且具有更高的灵活性，空间双臂系统的运动规划技术是研发空间双臂系统的一项关键技术。

目前，针对空间双臂系统的运动规划问题，往往采用遗传算法或粒子群算法等启发式算法进行寻优处理，然而采用启发式算法往往只能针对特定的一组空间机械臂初始构型与目标未知进行点对点的运动规划，而当空间机械臂初始构型或目标抓取点位置发生变化时，则需要从头开始重新进行一次运算，因此该方法的泛用性较差。

技术实现要素：

针对于上述现有技术的不足，本发明的目的在于提供一种基于深度强化学习的空间双臂系统约束运动规划方法，以解决现有技术中传统运动规划方法泛用性差，以及无约束的基于深度强化学习算法的运动规划方法造成的机械臂碰撞损伤等问题。

为达到上述目的，本发明采用的技术方案如下：

本发明的一种基于深度强化学习的空间双臂系统约束运动规划方法，步骤如下：

1)利用广义雅可比矩阵建立自由漂浮空间双机械臂系统的运动学模型；

2)基于上述的空间双臂系统的运动学模型，结合ddpg算法，设计空间双臂系统运动规划算法；

3)对ddpg算法中奖励函数进行设计，以实现对空间双臂系统运动规划算法中各约束条件的满足，包括机械臂末端执行机构的速度约束和双机械臂协同运动的自碰撞约束。

进一步地，所述步骤1)具体包括：根据下式(1)建立空间双机械臂系统的运动学模型：

其中，ⁱv0与ⁱω0分别为空间机械臂基座在惯性参考系下的速度矢量与角速度矢量；与分别为第1个机械臂在惯性参考系下的速度矢量与角速度矢量；与分别为第2个机械臂在惯性参考系下的速度矢量与角速度矢量；和分别为两臂各关节角的角速度；m为空间机械臂系统的质量矩阵，r0g＝rg-r0，rg表示系统质心位置，r0表示空间机械臂基座位置，算子×表示斜对称矩阵；j0和jφ为机械臂系统分别对关节角和基座的雅可比矩阵，其中：

式中，为第i关节的角速度方向矢量，为第i关节的位置矢量，为第i连杆的质心位置矢量，i为惯性张量矩阵。

进一步地，所述步骤2)具体包括：

21)在python编程环境中将上述建立的空间双机械臂系统的运动学模型构建为ddpg算法中的环境部分，与ddpg算法之间的信息交互，具体为：由ddpg算法生成具体需要执行的动作(即机械臂各关节的角速度信息)作为输入信息，输入到构建的上述环境部分中，通过运动学递推更新机械臂的状态信息，从而计算执行该动作所获得的即时奖励，最后由环境反馈更新后的机械臂状态信息、单步即时奖励以及是否已完成目标的标志位；

22)ddpg算法采用actor-critic模式，利用actor做出决策、critic做出评价：从环境中观测得到状态s，传递给actor根据所述状态s凭当前的策略网络做出决定得到动作a，将动作a作用于环境之后，给出当前步的奖励反馈r和新的状态，根据奖励反馈r，critic更新对actor的行为评价网络，actor再沿着critic建议的方向更新自身的策略网络，从而完成了一步训练，继续循环直到训练成功；ddpg采用记忆池的设计，将与环境交互得到的数据样本存储在记忆池中，再从中随机选择一条数据进行训练，打破数据间的关联，实现了样本的独立；ddpg采用四个神经网络：将actor对应的网络称为策略网络，分为现实策略网络和目标策略网络，将critic对应的网络称为价值网络即q网络，分为现实q网络和目标q网络；现实策略网络用于与环境进行交互，根据当前的状态s选择相应的动作a，并更新策略网络中的参数θ^μ；目标策略网络采用从记忆池中抽取的数据进行训练，完成根据下一状态s'选择合适的下一动作a'这一任务，该网络的网络参数θ^μ'定期从现实策略网络中进行复制更新；现实q网络用于计算当前的q值q(s,a|θ^q)和目标q值y＝r+γq′(s′,a′|θ^q')，并更新q网络中的参数θ^q；目标q网络用于计算目标q值中的q′(s′,a′|θ^q)，该网络的网络参数θ^q'定期从现实q网络中进行复制更新；

23)基于ddpg算法设计空间双臂系统约束运动规划算法包括以下步骤：

231)初始化现实策略网络与现实q网络的网络参数θ^μ与θ^q，并赋予目标策略网络与目标q网络相同的网络参数值；

232)初始化步骤21)中构建的环境；

233)根据当前的状态s选取动作a，将动作a作为环境的输入，在环境中执行动作a并给出下一时刻的状态s'、当前单步的即时奖励以及是否完成目标的标志位；

234)判断重放缓存区是否存满，若未存满，则将当前时刻状态、当前执行的动作、当前单步奖励以及下一时刻状态(s,a,r,s')存入重放缓存区，并使用s'更新s，继续执行步骤233)，若已存满，则将重放缓存区中最早的一组数据删除，并将当前时刻状态、当前执行的动作、当前单步奖励以及下一时刻状态(s,a,r,s')存入重放缓存区，继续执行步骤235)；

235)从重放缓存区中随机选取一批数据(s,a,r,s')，开始进行步骤22)中的训练过程，对网络参数进行更新并判断，若未完成目标或未到达设置的最大单回合步数，则继续执行步骤233)，若已完成目标或到达设置的最大单回合步数，则判断是否达到了最大回合数，若未达到，则继续执行步骤232)，若已达到，则结束。

进一步地，所述步骤3)具体包括：

31)机械臂运动规划的成功与否取决于机械臂末端执行器是否能够到达目标点，两个机械臂末端执行器与其对应的目标点之间的距离d1、d2是设计奖励函数的依据；设计一种线性函数与对数函数混合形式的奖励函数如下所示：

r＝-(d1+d2)-lg(d1+10^-8)-lg(d2+10^-8)(3)

其中，r表示奖励值，线性函数项为r＝k(d1+d2)，k为负常数，值为-1，用于保证两个机械臂末端执行机构有向其各自目标点靠近的趋势，而只使用线性函数形式的奖励函数只能保证部分收敛趋势，而很难保证两个末端执行机构同时精准地到达目标位置，因此添加对数函数项lg(d1+10^-8)-lg(d2+10^-8)，10^-8项用于避免对数函数产生奇异，同时约束对数函数项的最大值，用于在末端执行器到达目标点附近时，使其能够加速收敛到目标点处并获得该决策方法(即当末端执行器到达目标点附近时，做出决策让末端执行器加速向目标点靠近)；

32)对机械臂末端执行器速度设置如下约束：当机械臂末端执行器距离其对应的抓取目标点较远时，速度约束项对整体奖励没有影响；当机械臂末端执行器与其对应的抓取目标点之间的距离超过安全阈值后，距离越近，速度约束所能提供的惩罚就越大；为了满足这一要求，速度约束所对应的惩罚项设计为如下形式：

其中，rv表示速度约束对应的奖励值，和分别为两个末端执行器的速度，系数k1为距离对惩罚项大小的影响程度，系数k2为限制惩罚项的最大值，k1＝1,k2＝1；

33)当两个机械臂协同工作时，加入碰撞检测算法，具体如下：

假设s0,s1,t0,t1分别表示两条有向线段s和t的四个端点，ls和lt表示线段s和t所在的直线；sj,tj表示直线ls和lt的公垂线在这两条直线上的垂足；定义向量u＝s1-s0，v＝t1-t0，则使用这两个向量对垂足sj和tj进行表示：

其中，系数ks和kt分别表示垂足sj和tj在直线ls和lt上的位置；定义向量w0＝s0-t0,w＝sj-tj，结合上式(5)，w表示为如下形式：

向量w垂直于向量u和向量v，故有u·w＝0,w·v＝0，结合上式(6)和上述向量w与向量u和向量v的垂直关系，得到如下关系式：

令a＝u·u,b＝u·v,c＝v·v,d＝u·ω0,e＝v·ω0，则系数ks和kt通过上式(7)获得：

将系数ks和kt代入公式(5)即可求出垂足sj和tj的位置；当ac-b²＝0时，出现直线ls和lt平行或重合的情况，当两直线平行时，取kt＝0，即可求出一组垂足位置sj和tj，此时两线段之间的最小距离就是两个垂足之间的距离；当两直线重合时，不考虑线段重合的情况，则两线段之间的最小距离通过直接求解端点s0,s1与t0,t1之间距离的最小值获得；最终通过判断垂足与两线段之间的相对位置，即可求出两线段之间的最小距离dst，其具体形式如下式所示：

其中，dst表示点s到点t的最小距离，点s包括s0,s1,sj，点t包括t0,t1,tj；

34)根据上述步骤33)得到左机械臂上每一个连杆与右机械臂上每一个连杆之间的最小距离，再通过比较得到的最小距离得到其中的最小值dmin，即为左机械臂与右机械臂之间的最小距离，然后设计避免发生自碰撞的惩罚项函数；

在奖励函数中，两个机械臂之间最小距离dmin约束的惩罚项需要满足如下性质：当dmin足够大时，最小距离约束所提供的惩罚忽略；当dmin超过安全阈值时，随着dmin的减小，最小距离约束所提供的惩罚加重；最小距离约束的惩罚项采用与速度约束惩罚项相同的函数形式：

其中，rd表示最小距离约束对应的奖励值，最小距离约束惩罚项中的系数为：h1＝100,h2＝0.5；

35)结合步骤31)、32)与34)，得到考虑各约束条件的最终形式的奖励函数如下：

本发明的有益效果：

1、本发明利用广义雅各比矩阵描述空间双臂系统的运动学模型，能够准确描述基座自由漂浮的空间双臂系统末端执行器、基座的速度以及角速度与各关节的角速度之间的映射关系。

2、本发明利用强化学习算法进行空间双臂系统运动规划，显著提高了运动规划算法的泛用性。

3、本发明通过对强化学习算法的奖励函数进行合理的设计，使得运动规划算法能够满足一定的安全性约束，包括机械臂末端执行机构的速度约束以及双臂协同运动时的自碰撞约束，从而提高了规划运动轨迹的安全性。

附图说明

图1为本发明方法流程图；

图2为ddpg算法的原理图；

图3a为使用训练完成的网络抓取带自转卫星过程中第0秒效果图；

图3b为使用训练完成的网络抓取带自转卫星过程中第6秒效果图；

图3c为使用训练完成的网络抓取带自转卫星过程中第12秒效果图；

图3d为使用训练完成的网络抓取带自转卫星过程中第18秒效果图。

具体实施方式

为了便于本领域技术人员的理解，下面结合实施例与附图对本发明作进一步的说明，实施方式提及的内容并非对本发明的限定。

参照图1所示，本发明的一种基于深度强化学习的空间双臂系统约束运动规划方法，步骤如下：

1)利用广义雅可比矩阵建立自由漂浮空间双机械臂系统的运动学模型；

根据下式(1)建立空间双机械臂系统的运动学模型：

其中，ⁱv0与ⁱω0分别为空间机械臂基座在惯性参考系下的速度矢量与角速度矢量；与分别为第1个机械臂在惯性参考系下的速度矢量与角速度矢量；与分别为第2个机械臂在惯性参考系下的速度矢量与角速度矢量；和分别为两臂各关节角的角速度；m为空间机械臂系统的质量矩阵，r0g＝rg-r0，rg表示系统质心位置，r0表示空间机械臂基座位置，算子×表示斜对称矩阵；j0和jφ为机械臂系统分别对关节角和基座的雅可比矩阵，其中：

式中，为第i关节的角速度方向矢量，为第i关节的位置矢量，为第i连杆的质心位置矢量，i为惯性张量矩阵。

2)基于上述的空间双臂系统的运动学模型，结合ddpg(深度确定性策略梯度)算法，设计空间双臂系统运动规划算法；具体包括：

21)在python编程环境中将上述建立的空间双机械臂系统的运动学模型构建为ddpg算法中的环境部分，与ddpg算法之间的信息交互，具体为：由ddpg算法生成具体需要执行的动作(即机械臂各关节的角速度信息)作为输入信息，输入到构建的上述环境部分中，通过运动学递推更新机械臂的状态信息，从而计算执行该动作所获得的即时奖励，最后由环境反馈更新后的机械臂状态信息、单步即时奖励以及是否已完成目标的标志位；

22)参照图2所示，ddpg算法采用actor-critic模式，利用actor做出决策、critic做出评价：从环境中观测得到状态s，传递给actor根据所述状态s凭当前的策略网络做出决定得到动作a，将动作a作用于环境之后，给出当前步的奖励反馈r和新的状态，根据奖励反馈r，critic更新对actor的行为评价网络，actor再沿着critic建议的方向更新自身的策略网络，从而完成了一步训练，继续循环直到训练成功；ddpg采用记忆池的设计，将与环境交互得到的数据样本存储在记忆池中，再从中随机选择一条数据进行训练，打破数据间的关联，实现了样本的独立；ddpg采用四个神经网络：将actor对应的网络称为策略网络，分为现实策略网络和目标策略网络，将critic对应的网络称为价值网络即q网络，分为现实q网络和目标q网络；现实策略网络用于与环境进行交互，根据当前的状态s选择相应的动作a，并更新策略网络中的参数θ^μ；目标策略网络采用从记忆池中抽取的数据进行训练，完成根据下一状态s'选择合适的下一动作a'这一任务，该网络的网络参数θ^μ'定期从现实策略网络中进行复制更新；现实q网络用于计算当前的q值q(s,a|θ^q)和目标q值y＝r+γq′(s′,a′|θ^q')，并更新q网络中的参数θ^q；目标q网络用于计算目标q值中的q′(s′,a′|θ^q)，该网络的网络参数θ^q'定期从现实q网络中进行复制更新；

23)基于ddpg算法设计空间双臂系统约束运动规划算法包括以下步骤：

231)初始化现实策略网络与现实q网络的网络参数θ^μ与θ^q，并赋予目标策略网络与目标q网络相同的网络参数值；

232)初始化步骤21)中构建的环境；

233)根据当前的状态s选取动作a，将动作a作为环境的输入，在环境中执行动作a并给出下一时刻的状态s'、当前单步的即时奖励以及是否完成目标的标志位；

234)判断重放缓存区是否存满，若未存满，则将当前时刻状态、当前执行的动作、当前单步奖励以及下一时刻状态(s,a,r,s')存入重放缓存区，并使用s'更新s，继续执行步骤233)，若已存满，则将重放缓存区中最早的一组数据删除，并将当前时刻状态、当前执行的动作、当前单步奖励以及下一时刻状态(s,a,r,s')存入重放缓存区，继续执行步骤235)；

235)从重放缓存区中随机选取一批数据(s,a,r,s')，开始进行步骤22)中的训练过程，对网络参数进行更新并判断，若未完成目标或未到达设置的最大单回合步数，则继续执行步骤233)，若已完成目标或到达设置的最大单回合步数，则判断是否达到了最大回合数，若未达到，则继续执行步骤232)，若已达到，则结束。

3)对ddpg算法中奖励函数进行设计，以实现对空间双臂系统运动规划算法中各约束条件的满足，包括机械臂末端执行机构的速度约束和双机械臂协同运动的自碰撞约束；

31)机械臂运动规划的成功与否取决于机械臂末端执行器是否能够到达目标点，两个机械臂末端执行器与其对应的目标点之间的距离d1、d2是设计奖励函数的依据；设计一种线性函数与对数函数混合形式的奖励函数如下所示：

r＝-(d1+d2)-lg(d1+10^-8)-lg(d2+10^-8)(3)

其中，r表示奖励值，线性函数项为r＝k(d1+d2)，k为负常数，值为-1，用于保证两个机械臂末端执行机构有向其各自目标点靠近的趋势，而只使用线性函数形式的奖励函数只能保证部分收敛趋势，而很难保证两个末端执行机构同时精准地到达目标位置，因此添加对数函数项lg(d1+10^-8)-lg(d2+10^-8)，10^-8项用于避免对数函数产生奇异，同时约束对数函数项的最大值，用于在末端执行器到达目标点附近时，使其能够加速收敛到目标点处并获得该决策方法(即当末端执行器到达目标点附近时，做出决策让末端执行器加速向目标点靠近)；

32)对机械臂末端执行器速度设置如下约束：当机械臂末端执行器距离其对应的抓取目标点较远时，速度约束项对整体奖励没有影响；当机械臂末端执行器与其对应的抓取目标点之间的距离超过安全阈值后，距离越近，速度约束所能提供的惩罚就越大；为了满足这一要求，速度约束所对应的惩罚项设计为如下形式：

其中，rv表示速度约束对应的奖励值，和分别为两个末端执行器的速度，系数k1为距离对惩罚项大小的影响程度，系数k2为限制惩罚项的最大值，k1＝1,k2＝1；

33)当两个机械臂协同工作时，加入碰撞检测算法，考虑到以下原因：1、通过机械臂的运动学参数可以看出，机械臂的半径相对于长度来说是可以忽略的；2、由于需要在算法的每一步中都进行碰撞检测运算，所以复杂的模型必然会带来庞大的计算量，甚至可能会导致算法无法运行。同时ddpg算法需要进行大量的迭代运算，碰撞检测算法的设计也需要尽量简化，因此，选取一种基于向量运算的方法来进行两臂之间最短距离的计算；具体如下：

假设s0,s1,t0,t1分别表示两条有向线段s和t的四个端点，ls和lt表示线段s和t所在的直线；sj,tj表示直线ls和lt的公垂线在这两条直线上的垂足；定义向量u＝s1-s0，v＝t1-t0，则使用这两个向量对垂足sj和tj进行表示：

其中，系数ks和kt分别表示垂足sj和tj在直线ls和lt上的位置；定义向量w0＝s0-t0,w＝sj-tj，结合上式(5)，w表示为如下形式：

向量w垂直于向量u和向量v，故有u·w＝0,w·v＝0，结合上式(6)和上述向量w与向量u和向量v的垂直关系，得到如下关系式：

令a＝u·u,b＝u·v,c＝v·v,d＝u·ω0,e＝v·ω0，则系数ks和kt通过上式(7)获得：

将系数ks和kt代入公式(5)即可求出垂足sj和tj的位置；当ac-b²＝0时，出现直线ls和lt平行或重合的情况，当两直线平行时，取kt＝0，即可求出一组垂足位置sj和tj，此时两线段之间的最小距离就是两个垂足之间的距离；当两直线重合时，不考虑线段重合的情况，则两线段之间的最小距离通过直接求解端点s0,s1与t0,t1之间距离的最小值获得；最终通过判断垂足与两线段之间的相对位置，即可求出两线段之间的最小距离dst，其具体形式如下式所示：

其中，dst表示点s到点t的最小距离，点s包括s0,s1,sj，点t包括t0,t1,tj；

34)根据上述步骤33)得到左机械臂上每一个连杆与右机械臂上每一个连杆之间的最小距离，再通过比较得到的最小距离得到其中的最小值dmin，即为左机械臂与右机械臂之间的最小距离，然后设计避免发生自碰撞的惩罚项函数；

在奖励函数中，两个机械臂之间最小距离dmin约束的惩罚项需要满足如下性质：当dmin足够大时，最小距离约束所提供的惩罚忽略；当dmin超过安全阈值时，随着dmin的减小，最小距离约束所提供的惩罚加重；最小距离约束的惩罚项采用与速度约束惩罚项相同的函数形式：

其中，rd表示最小距离约束对应的奖励值，最小距离约束惩罚项中的系数为：h1＝100,h2＝0.5；

35)结合步骤31)、32)与34)，得到考虑各约束条件的最终形式的奖励函数如下：

采用上式所述的奖励函数对网络进行训练，使用训练完成的网络抓取带自旋卫星的全过程效果图如图3a-图3d所示。

本发明基于深度强化学习的空间双臂系统，采用深度强化学习模型，只需要选取一个合理的机械臂初始构型和目标抓取点位置的范围，通过训练，即使在该范围内任意选定机械臂初始构型和目标抓取点位置，也可以实时地规划出合理的运动路径，因此能够很好地提高规划算法的泛用性。然后，由于没有考虑各类约束问题，该方法规划出地运动路径往往存在两机械臂之间发生碰撞或机械臂与目标之间发生碰撞等问题，可能会造成机械臂的损伤。

本发明具体应用途径很多，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进，这些改进也应视为本发明的保护范围。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除