基于反演法的不确定性机器人自适应神经网络控制方法与流程

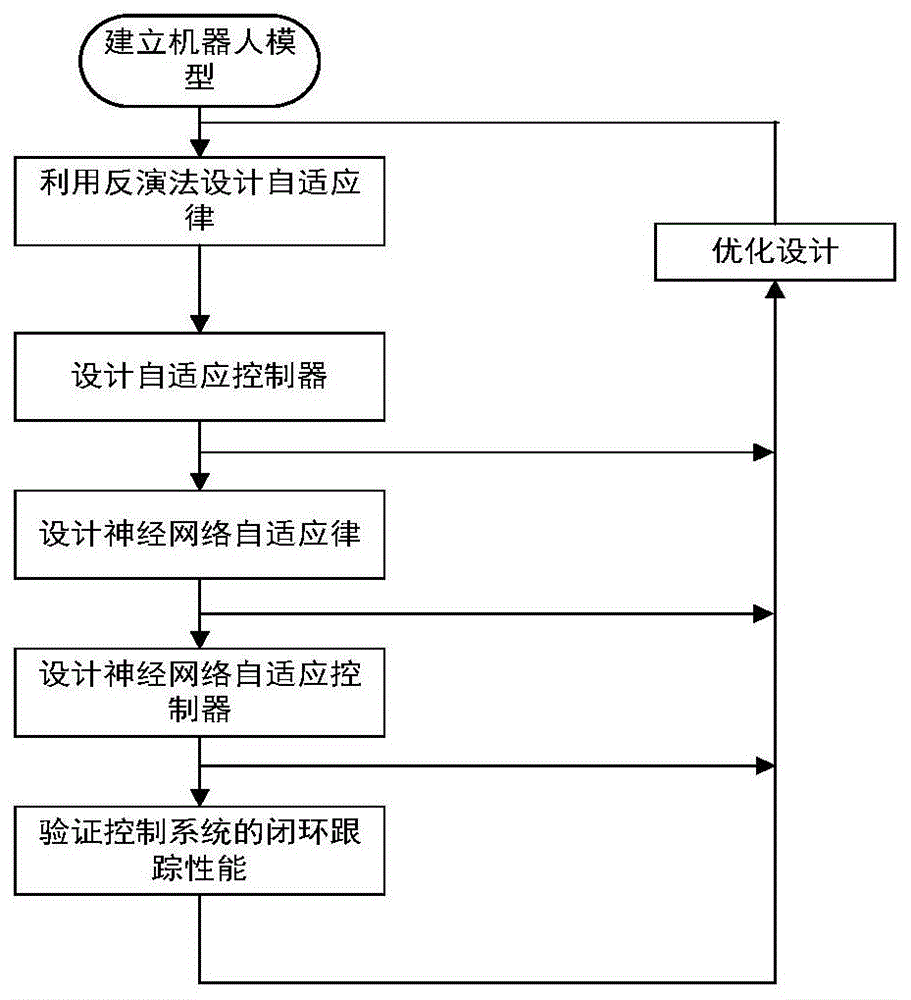
本发明属于机器人轨迹跟踪控制技术领域，具体涉及一种基于反演法的不确定性机器人自适应神经网络控制方法。

背景技术：

当机器人的结构及其机械参数确定时，可以通过动力学模型描述系统完整的动态特性，从而应用各种控制理论，设计基于模型的控制器，实现机器人的轨迹跟踪控制，使得机器人的位置、速度等状态变量跟踪给定的理想轨迹。但是在实际工程中，由于机器人是一个非线性和不确定性系统，很难得到机器人精确的数学模型。因此，对系统非线性不确定性的处理是机器人轨迹跟踪控制中非常关键的研究内容。

目前，自适应控制技术研究在机器人控制系统中取得了丰硕的成果。但就目前热门的研究成果来说，仍存在以下问题：

针对机器人具有建模误差、外部扰动等不确定性的问题，自适应控制能够根据被控对象的参数变化以及实际输出情况进行辨识、学习，从而对控制律结构和参数做出调整，实现一定的控制性能指标。但是这种在线辨识方法计算量庞大，实时性要求高，对于存在不确定性复杂系统，自适应控制不能保证系统的稳定性。采用神经网络实现对机器人动力学方程中未知部分的精确逼近，从而保证了系统的稳定性。

技术实现要素：

本发明解决的技术问题是：为了解决现有技术的不足，针对机器人具有建模误差、外部扰动等不确定性的问题，提供了一种能够对未知模型的参数变化和实际输出情况进行精确估计和实时调整，并可以使系统具有自主消除模型不确定性影响的能力，从而使得机器人的位置、速度以及加速度等变量具有理想的跟踪状态。

为解决上述问题，本发明的技术解决方案提出基于反演法的不确定性机器人自适应神经网络控制方法，通过以下步骤实现：

步骤一、建立不确定性机器人的动力学模型，具体如下：

其中，q，分别表示关节位置，速度和加速度；表示正定的惯性矩阵，为关节力或力矩；表示离心力项和科氏力项；表示重力项；j(q)为非奇异雅可比矩阵；表示外部干扰；

步骤二、将不确定性机器人的动力学模型转化为一般的状态空间形式，具体如下：

其中x1＝q，

步骤三、定义跟踪误差，并将步骤二中的一般状态空间形式转化为关于误差的状态空间形式，具体如下：

z1＝x1-α1

z2＝x2-α2

其中，α1为机器人关节的理想轨迹，α2为虚拟控制输入。

步骤四、利用反演法设计基于模型的控制器，具体如下：

选取barrier李雅普诺夫函数:

其中，kci表示一个正常数且满足|z1i|<kci,(i＝1,2,…,n)。

对v1(t)求导可得：

其中，β2i是一个虚拟控制输入并且满足以下等式关系：

其中，

利用反演法设计v2(t)，可得：

对v2(t)求导可得：

将误差模型代入可得：

步骤五、引入moore-penrose逆，并设计控制律τ0，具体如下：

当z2＝[0,0,…,0]^t时，当z2≠[0,0,…,0]^t时，设计控制律为

其中，kp＝diag(kp1,kp2,…,kpn)；kp是一个正常数。

将上式代入中可得：

步骤六、在考虑动力学模型和外部扰动不确定的情况下，利用神经网络设计自适应控制器，具体如下：

其中，w＝[w1,w2,…,wn]^t为神经网络的权值；sz＝[s(z)1,s(z)2,…,s(z)n)]^t表示基础函数；表示神经网络的输入；为估计误差。

设计自适应律为：

其中，wi^*分别为神经网络的权值误差，估计值，实际值；表示常数增益矩阵；σi>0(i＝1,2,…,n)表示极小的正常数。

设计控制律：

本发明与现有技术相比有益效果为：

(1)本发明研究提供的神经网络自适应轨迹跟踪方法及控制器，并且充分考虑了外部环境产生的扰动，以及机器人建模不确定性，对于提高机器人控制系统对不确定性因素的自适应能力更具有实际意义；

(2)本发明研究提出自适应控制与神经网路控制相结合的控制策略，利用自适应控制辨识系统的不确定信息，通过神经网络替代所述轨迹跟踪系统的不确定项，引入自适应律对控制器进行相应的调节，保证了系统的稳定性，而且通过自适应控制即时调整控制规律和参数提高了系统的动态性能。

附图说明

图1是本发明的自适应神经网络方法流程图；

图2是两关节机械臂系统；

图3是机械手各关节的位置跟踪效果；

图4是机械手各关节的速度跟踪效果；

图5是机械手各关节的位置跟踪误差；

图6是机械手各关节的速度跟踪误差。

具体实施方式

现结合附图对本发明的具体实施方式做进一步详细的说明。为了本领域普通技术人员可以更好地了解本发明的实施，本发明还提供了利用matlab2012b软件进行轨迹跟踪的仿真验证结果。

如图1所示，当姿态传感器发生故障时，为了使柔性航天器能够跟踪上期望姿态，通过未知输入观测器和滤波器建立故障诊断与辨识模块，对故障进行实时检测与估计，进一步利用故障估计信息设计动态输出反馈容错控制器，提高柔性航天器姿态控制系统对故障的容忍能力。

本发明一种基于动态输出反馈控制的柔性航天器主动容错控制方法，包括以下步骤：

步骤一、建立不确定性机器人的动力学模型，具体如下：

其中，q，表示关节位置，速度和加速度；表示正定的惯性矩阵，为关节力或力矩；表示离心力项和科氏力项；表示重力项；j(q)为非奇异雅可比矩阵；表示外部干扰；

步骤二、将不确定性机器人的动力学模型转化为一般的状态空间形式，具体如下：

其中x1＝q，

步骤三、定义跟踪误差，并将步骤二中的一般状态空间形式转化为关于误差的状态空间形式，具体如下：

z1＝x1-α1

z2＝x2-α2

其中，α1为机器人关节的理想轨迹，α2为虚拟控制输入。

步骤四、利用反演法设计基于模型的控制器，具体如下：

选取barrier李雅普诺夫函数:

其中，kci表示一个正常数且满足|z1i|<kci,(i＝1,2,…,n)。

对v1(t)求导可得：

其中，β2i是一个虚拟控制输入并且满足以下等式关系：

其中，

利用反演法设计v2(t)，可得：

对v2(t)求导可得：

将误差模型代入可得：

步骤五、引入moore-penrose逆，并设计控制律τ0，具体如下：

当z2＝[0,0,…,0]^t时，当z2≠[0,0,…,0]^t时，设计控制律为

其中，kp＝diag(kp1,kp2,…,kpn)；kp是一个正常数。

将上式代入中可得：

步骤六、在考虑动力学模型和外部扰动不确定的情况下，利用神经网络设计自适应控制器，具体如下：

其中，w＝[w1,w2,…,wn]^t为神经网络的权值；sz＝[s(z)1,s(z)2,…,s(z)n)]^t表示基础函数；表示神经网络的输入；为估计误差。

设计自适应律为：

其中，wi^*分别为神经网络的权值误差，估计值，实际值；表示常数增益矩阵；σi>0(i＝1,2,…,n)表示极小的正常数。

设计控制律：

通过以下步骤验证上述控制器是否稳定：

一、定义lyapunov函数：

对lyapunov函数进行求导，可得如下不等式：

令

则

根据杨氏不等式：

其中ε＝ε(z)且

由此可以得到

其中ρ是v3的系数，c表示一个常数。

因此，通过上述不等式条件可验证系统的稳定性。

下面以具体仿真实验，以验证本实施例提供的轨迹跟踪控制方法的有效性

(1)机器人动力学模型的具体仿真参数如下：

其中，m1和m2分别为机械臂两个关节的质量；l1和l2为机械臂杆的长度；q1和q2分别为两关节转动角度。

(2)仿真参数选取：

m1＝1kg，m2＝2kg，l1＝1m，l2＝0.5m

假设关节初始状态为

系统期望轨迹为qd＝[sin(t),sin(t)]^t

结果说明：

如图3和图4所示，机械手都能够成功达到所期望的轨迹，验证了机械手存在不确定项时，该方法能够进行有效的控制；

如图5和图6所示，系统的跟踪误差能够收敛到一个接近于0的极小值；

通过以上仿真结果图的分析比较，可以看出，本发明提供的自适应神经网络控制方法能够有效消除不确定性影响，改善了系统的轨迹跟踪性能，具有良好的稳定性和动态性能。

以上所述，仅为本发明中的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉该技术的人在本发明所揭露的技术范围内，可理解想到的变换或替换，都应涵盖在本发明的包含范围之内，因此，本发明的保护范围应该以权利要求书的保护范围为准。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除