三自由度转动曲柄连杆并联平台位姿控制方法与流程
 2021-01-19 14:01:09|
2021-01-19 14:01:09| 288|
288| 起点商标网
起点商标网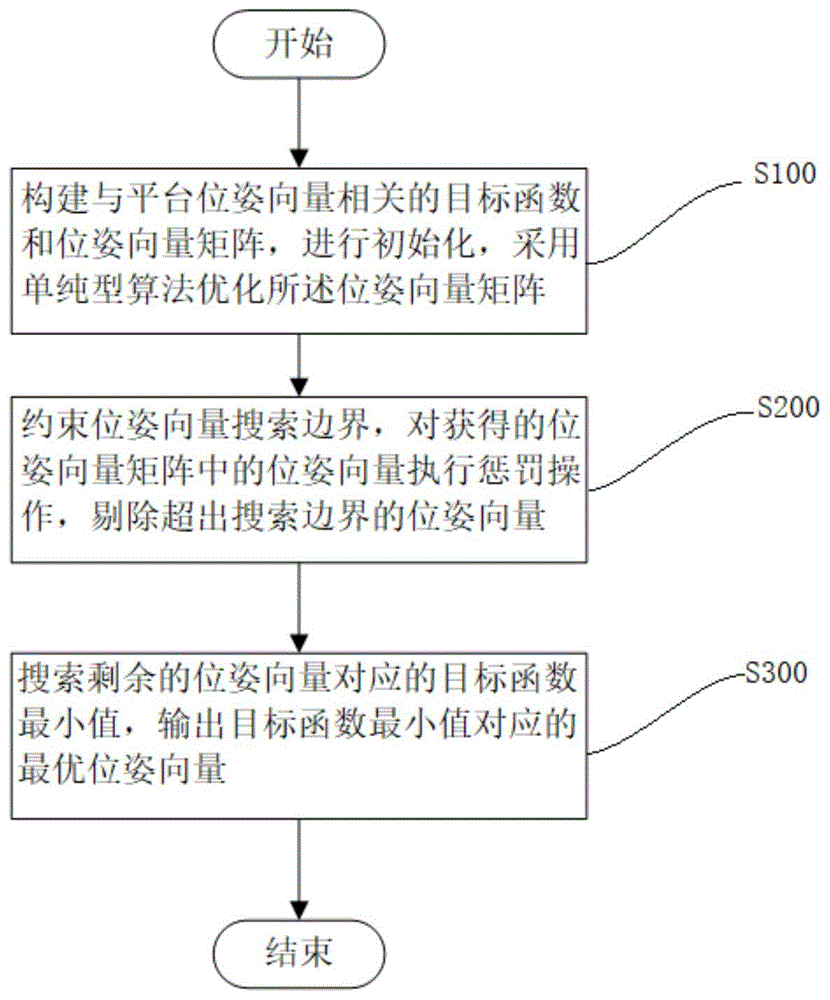
本发明涉及并联机器人运动学领域,具体涉及一种三自由度转动曲柄连杆并联平台位姿控制方法。
背景技术:
并联机器人是机器人中重要的一类,具备机构紧凑、刚度高、负载能力强等优势。其中,三自由度转动曲柄连杆(简称3-rss/s)并联平台被广泛应用于航天、医疗和工业装配领域,其精确定姿和力学响应特性正是当下研究与应用的热点,而平台位姿监控是这些研究中不可或缺的技术环节。在实际生产中,由于安装传感器会较大地限制平台行程范围,因此直接测算平台位姿的方法往往难以满足使用要求,依靠促动器末端驱动量信息,通过正运动学求解平台位姿的方法往往更具应用前景。但是,三自由度并联平台正运动学求解的难点主要在于:并联机构正运动学无法直接求解,往往需通过逆解迭代或解析雅克比矩阵的方法求解,而在实际应用中机构驱动端输入量测量存在扰动,使得传统算法难以保证求解的准确性和稳定性;训练评估与反馈对平台位姿信息获取的实时性要求较高,需要正解求解算法快速收敛,而依据现有技术,三自由度转动曲柄连杆并联平台逆解模型依赖二元二次方程组建立,需要根据促动器相角范围判断可行解,这使得构建正运动学解析解的难度加大,迭代寻优法是正解模型构建的首选手段,但由于工程应用中对实时性的要求和测量误差的限制,亟需设计一种收敛讯速、精度高和抗扰能力强的寻优算法。
技术实现要素:
本发明针对目前现有技术中的上述问题,提出一种适用于三自由度转动曲柄连杆并联平台的正解求解优化方法法,该方法基于三自由度转动曲柄连杆并联平台运动特性,以三转动促动器驱动量为输入,以平台旋转位姿为输出,具备收敛速度快,求解精度高,抗扰能力强的优势。
本发明的目的通过以下的技术方案实现:三自由度转动曲柄连杆并联平台位姿控制方法,包括以下步骤:
s100、构建与平台位姿向量相关的目标函数和位姿向量矩阵,进行初始化,采用单纯型算法优化所述位姿向量矩阵;
s200、约束位姿向量搜索边界,对优化获得的位姿向量矩阵中的位姿向量执行惩罚操作,剔除超出搜索边界的位姿向量;
s300、搜索剩余的位姿向量对应的目标函数最小值,输出目标函数最小值对应的最优位姿向量。
进一步地,所述s100中,根据三自由度转动曲柄连杆的机械结构和运动学逆解理论,建立逆解数学模型s=inv(pj),其中,s为逆解得到的曲柄连杆促动器的角度变化量,pj为平台位姿向量集,构建目标函数f(pj)=(inv(pj)-s0)2,其中,s0为曲柄连杆促动器的角度变化量实测值。
进一步地,所述s100中,任意选取平台上的至少三个点,以至少三个点的n组位姿向量参数为元素构建位姿向量矩阵,完成位姿向量矩阵初始化。
进一步地,所述s200的具体步骤包括:
s201、建立惩罚函数:
s202、根据s201建立的惩罚函数,对位姿向量重新赋值。
进一步地,所述s300之前还包括s210、执行回溯操作。
进一步地,所述回溯操作的具体步骤包括:s211、对位姿向量进行逆解求解曲柄连杆促动器角度变化量,判断能否获得有效的角度变化量;s212、根据回溯函数:
进一步地,s300之后还包括步骤s400:判断s300中获得的位姿向量对应的目标函数值是否小于预设的最大允许误差值,如果是,则输出该位姿向量,得到最优解。
进一步地,如果判断结果为否,则采用粒子群算法搜索全局后,返回s300。
本发明的有益效果:
1、本发明的求解方法在粒子群算法基础上加入单纯形算法,并且采用惩罚函数算法,避免寻优过程超出边界,以解决机构极限行程外正解无解,致使搜索算法不收敛的情况,能够实现快速收敛;
2、本发明的求解过程中通过对位姿向量逆解求解促动器的角度变化值,可避免位姿传感器的使用,并避免传感器数据传输线对并联平台运动范围的影响,具有强的抗干扰能力。
附图说明
图1为本发明的三自由度转动曲柄连杆并联平台位姿控制方法流程图;
图2为三自由度转动曲柄连杆并联平台的机械结构图,其中,a-动平台,b-定平台,e2-第三定杆,f2-第四定杆,b2-第二约束球铰,a2-第四定杆与第二促动器的连接点,c1-第一定杆与动平台a的连接点,c2-第三定杆与动平台的连接点,c3-第五定杆与动平台a的连接点,411-第七定杆,412-第八定杆,o1-第四约束球铰,2-第二促动器;
图3为三自由度转动曲柄连杆与并联平台上各点在三自由度转动曲柄连杆并联平台坐标系中的位置示意图;
图4为第二驱动支链和中间约束支链上各点在三自由度转动曲柄连杆并联平台坐标系以及建模坐标系中的位置示意图;
图5为本发明的三自由度转动曲柄连杆并联平台另一位姿控制方法流程图。
具体实施方式
下面结合附图和具体实施例,对本发明的技术方案进行清楚,完整地描述。
具体实施例1:结合图1~图4说明本实施例,三自由度转动曲柄连杆并联平台位姿控制方法,如图1所示,包括以下步骤:
s100、构建与平台位姿向量相关的目标函数和位姿向量矩阵,进行初始化,采用单纯型算法优化所述位姿向量矩阵;
s200、约束位姿向量搜索边界,对优化获得的位姿向量矩阵中的位姿向量执行惩罚操作,剔除超出搜索边界的位姿向量;
s300、搜索剩余的位姿向量对应的目标函数最小值,输出目标函数最小值对应的最优位姿向量。惩罚函数算法的引入,避免寻优过程超出边界,以解决机构极限行程外正解无解,致使搜索算法不收敛的情况,能够实现快速收敛。
在一个实施例中,s100中根据三自由度转动曲柄连杆的机械结构和运动学逆解理论,建立逆解数学模型,进而构建目标函数。
例如,根据三自由度转动曲柄连杆的机械结构和运动学逆解理论,建立逆解数学模型s=inv(pj),其中,s为逆解得到的曲柄连杆促动器的角度变化量,pj为平台位姿向量集,如图2,三自由度转动曲柄连杆并联平台由动平台a、定平台b、三路驱动支链和中间约束支链构成。其中三路驱动支链包括第一驱动支链、第二驱动支链和第三驱动支链,第一驱动支链由第一定杆、第二定杆和第一约束球铰(图中未示出)组成,第二驱动支链由第三定杆e2、第四定杆f2和第二约束球铰b2组成,第三驱动支链由第五定杆定杆、第六定杆和第三约束球铰(图中未示出)组成,中间约束支链由第七定杆411、第八定杆412及第四约束球铰o1组成。第一定杆、第三定杆e2以及第五定杆与动平台a的连接点分别为c1、c2和c3;在图3或图4中,a1为第二定杆与第一促动器(图中未示出)的连接点,a2为第四定杆f2与第二促动器2的连接点,且为平台b上的点,a3为第六定杆与第三促动器(图中未示出)的连接点;定平台b固定不动,动平台a绕第四约束球铰o1只可实现三个方向的转动运动。三自由度转动曲柄连杆并联平台坐标系(xyz)如图3中所示,其中,以o为原点,x轴与至a2点所在直线平行;x、y所在平面与静平台所在平面平行,z轴竖直向上。如图4所示,动平台a的建模坐标(xyz)定义为:以第四约束球铰o1抽象成的点为原点,z轴与定平台b垂直,方向竖直向上,x轴方向与定平台b所在平面平行,对应三自由度转动曲柄连杆并联平台+x轴,y轴由右手定则确定。
三自由度转动曲柄连杆并联平台中所指俯仰运动角θ为动平台a所在平面绕y轴运动,偏摆运动角ψ为动平台a所在平面绕z轴运动,横滚运动角
利用逆解模型得到的第一促动器、第二促动器2和第三促动器的角度变化定义为s=[σ1σ2σ3]t,角度变化的实际测量值定义为
rb为定平台b上的点ai(i=1,2,3)到三自由度转动曲柄连杆并联平台坐标系原点o的距离,ra为动平台a上的点ci(i=1,2,3)到点o2的距离,点o2为建模坐标系的原点o1在动平台a上的正投影,h为动平台a与定平台b平行时两平台的间距,h0为三自由度转动曲柄连杆并联平台坐标系原点o点到建模坐标系的原点o1点的距离。
定平台b上的点a1、a2、a3相对于中三自由度转动曲柄连杆并联平台坐标系的坐标分别为:
χa1:(rb·cos30,-rb·sin30,0),
χa2:(-rb,0,0),
χa3:(rb·cos30,rb·sin30,0),
动平台a上的点c1、c2、c3在建模坐标系内的坐标分别为:
χc1:(ra·cos30,-ra·sin30,h-h0);
χc2:(-ra·cos30,0,h-h0);
χc3:(ra·cos30,-ra·sin30,h-h0);
将建模坐标系下点c1、c2、c3坐标转换为三自由度转动曲柄连杆并联平台坐标系下坐标的转换公式如下:
γci=r·χci+[0,0,h0]
b1、b2、b3在三自由度转动曲柄连杆并联平台坐标系下的坐标分别为:
χb1=χa1+(l1·cosσ1·cos30,-l1·cosσ1·sin30,l1·sinσ1);
χb2=χa2+(0,l1·cosσ2,l1·sinσ2);
χb3=χa3+(-l1·cosσ3·cos30,-l1·cosσ3·sin30,l1·sinσ3);
其中,σ1、σ2和σ3分别表示点a1、a2和a3处电机转角变化。l1代表定杆fi(i=1,2,3)的长度,根据式(2)和(3),利用数学公式表达三自由度转动曲柄连杆并联平台的运行学逆解数学模型:
l2=(χbi[1]-χci[1])2+(χbi[2]-χci[2])2+(χbi[3]-χci[3])2(i=1,2,3)i=1,2,3(4)
(sinσi)2+(cosσi)2=1(5)
i代表的是i个驱动支链,其中,i=1,2,3。l2表示定杆ei的长度,其中,i=1,2,3。
为便于阐述,采用逆解模型s=inv(pj),其中,i=1,2,3替代公式(4)和公式(5),表示利用逆解模型求解第一促动器(图中未示出)、第二促动器2和第三促动器(图中未示出)的角度变化,构建目标函数f(pj)=(inv(pj)-s0)2。
其次,定义平台的位姿矩阵
最后,采用单纯形法执行寻优操作:寻找位姿矩阵中对应目标函数值最大的三个位姿向量,取其中一位姿向量pn,位姿向量pn对应目标函数值为f(pn),对位姿向量pn进行反射操作:定义反射位姿向量为pnr,pnr对应的目标函数值记为f(pnr),令pnr=pnc+λ(pnc-pn),其中,反射系数λ=1;
计算并比较f(pnr)和f(pnb),如果f(pnr)<f(pnb),则反射方向正确,执行扩张操作:定义扩张位姿向量pne,pne对应的函数值记为f(pne),令pne=pnc+ω(pnr-pnc),其中,扩张系数ω=1.8,计算f(pne)并与f(pnb)比较,判断f(pne)<f(pnb)是否成立,
是,则用pne取代pn;
否,则用pnr取代pn;
如果f(pnr)>f(pnb),则反射方向不正确,执行压缩操作:定义压缩位姿向量pnt,pnt对应的函数值记为f(pnt),令
是,则用pnt取代步pn;
否,则pn的值保持不变;
如果f(pnr)=f(pnb),则pn的值保持不变;
比较函数值f(pn)、f(pnr)和f(pnb)的大小,并判断f(pn)>f(pnr)>f(pnb)是否成立,
如果f(pn)>f(pnr)>f(pnb)成立,则执行收缩操作:定义收缩位姿向量pnw,pnw对应的函数值记为f(pnw),令pnw=pnc-α(pn-pnc),其中,收缩系数α=0.6,计算f(pnw)的值并与f(pn)比较,判断f(pnw)<f(pn)是否成立,如果:
是,则用pnw取代pn;
否,则pn的值保持不变;
如果f(pn)>f(pnr)>f(pnb)不成立,则pn的值保持不变,执行下一步骤,根据重新获得的最优位姿向量优化初始位姿向量矩阵q0中的各个元素,获得新的位姿向量矩阵q′;
在本发明的其他实施例中,步骤s100可以通过其他方式实现,例如选取平台上4个、5个或更多的点的位姿向量参数来构建位姿矩阵;或者选取8组、9组或者更多组位姿向量构建初始位姿矩阵;或者在寻优过程中,反射系数选取0.9或1.1或其他能够实现收缩操作的数值,扩张系数选取1.7或1.9或其他能够实现扩张操作的数值,压缩系数选择0.5或0.7或者其他能够实现压缩操作的数值,收缩系数选择0.5或者0.7或其他能够实现收缩操作的数值。
在本发明的另一个实施例中,s200的具体步骤可以包括:
s201、构建惩罚函数:
s202、根据s201中所构建的惩罚函数,对s100中获得的最优位姿向量重新赋值。
引入惩罚函数的作用是剔除超出搜索边界的位姿向量,在本发明的其他实施例中,惩罚操作可以通过其他方式例如构建其他可以使边界收敛的惩罚函数实现。
如图5所示,本发明的另一实施例在具体实施例1的基础上进一步改进,所述s300之前还可以包括s210、执行回溯操作:
s211、对位姿向量进行逆解求解曲柄连杆促动器角度变化量,判断能否获得有效的角度变化量;
s212、根据回溯函数:
回溯操作的作用是解决位姿向量逆解无有效解的异常情形,在本发明的其他实施例中,可以构建其他能够实现相同作用的回溯函数。
在本发明的另一个实施例中,s300的之后还包括步骤s400:判断s300中获得的最优位姿向量对应的目标函数值是否小于预设的最大允许误差ε,如果是,则输出该最优位姿向量。
本发明的另一个实施例中,s400中,如果判断结果为最优位姿向量对应的目标函数值大于或等于预设的最大允许误差ε,则采用粒子群算法依据公式:
搜索界限内全部位姿向量,其中,
需要说明的是,以上实施例仅用于解释说明本发明的技术方案,并不用于限定本发明的保护范围,凡未脱离本发明技艺精神所作的等效实施例或变更均应包含在本发明的保护范围之内。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



