基于有限时间跟踪控制的协作机器人控制方法与流程
 2021-01-19 13:01:40|
2021-01-19 13:01:40| 313|
313| 起点商标网
起点商标网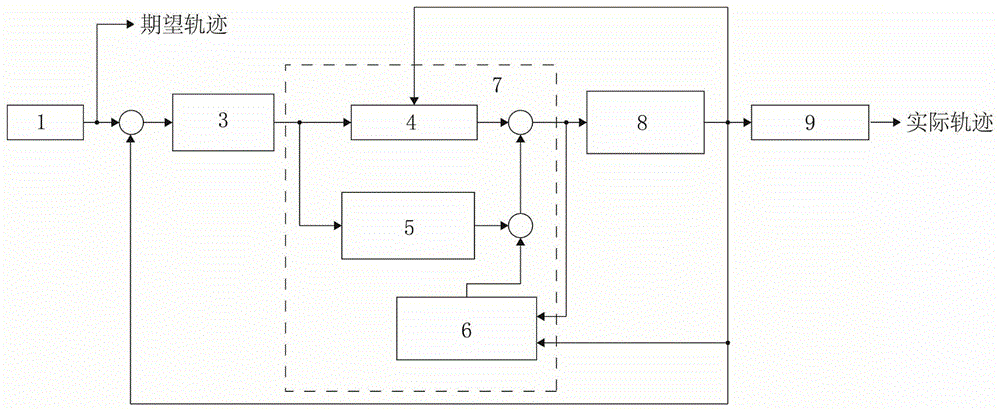
本发明涉及一种基于有限时间跟踪控制的协作机器人控制方法,应用于协作机器人的运动控制领域。
背景技术:
协作机器人是机器人应用的一个重要分支,主要应用于医疗康复、人机协同工作等领域。相对于传统的工业机器人,协作机器人具有体积小、高负载自重比、低速安全、灵活性高等特点。协作机器人控制系统的设计不仅要满足常规机器人的功能需求,还要具备人与机器人之间进行力交互的能力。更重要的是,在人机交互过程中需要确保人的安全。目前而言,协作机器人仍处于起步阶段,但工业机器人已经发展多年,积累了丰富的技术与经验,对协作机器人的发展将会提供很有利的帮助。
协作机器人是一个复杂的控制系统,具有多输入多输出、强耦合性、快时变性和非线性等特点,并且存在模型不精确、参数变化、摩擦、外部干扰等不确定性因素的影响。不确定性容易降低协作机器人控制系统的控制性能和稳定性,因此有效地抑制不确定性对控制系统的影响是跟踪控制器设计的关键。近年来,扰动观测器技术被广泛用于处理控制系统的不确定性。扰动观测器的输出可以用于干扰的前反馈补偿,由于这种方法具有前反馈的特性,扰动观测器不需要使用较大的反馈增益就可以提供快速的跟踪效果及平滑的控制动作。另一方面,传统的滑模控制器常采用的是线性滑模切换面,该切换面的特点是当系统的状态变量靠近平衡点时,控制器迫使系统状态变量达到平衡点的速度较慢,即渐进收敛性。因此,如何有效地提高协作机器人控制系统的全局快速收敛性也是控制系统设计的关键。
技术实现要素:
本发明的目的在于克服已有技术存在的不足,提供一种基于有限时间跟踪控制的协作机器人控制方法,利用非线性扰动观测器逼近并且补偿控制系统中存在的集中扰动量,利用非奇异快速终端滑模切换函数设计等效控制器,特点是收敛速度快及具有全局快速收敛特性。另外,设计二阶滑模控制器,用于补偿非线性扰动观测器的逼近误差,同时有助于增强控制系统的稳定性和抗干扰能力。
为达到上述目的,本发明采用如下技术方案:
一种基于有限时间跟踪控制的协作机器人控制方法,操作步骤如下:
a.建立协作机器人的动力学模型:
针对协作机器人,以关节为研究对象,利用拉格朗日法求解协作机器人的动力学模型,通过以下所示的二阶微分方程表示:
式中,
式中,τdis(t,q)定义为一个集中扰动向量,表达式如下所示:
式中,δm(q),
b.设计非线性扰动观测器:
记
式中,
定义辅助变量z如下:
式中,函数向量
结合式(4),对式(5)求导得:
令
将式(7)代入到式(6)中可得:
因此,非线性扰动观测器设计为:
其中:
式中,
c.设计协作机器人有限时间跟踪控制器:
定义协作机器人的关节角度误差函数e(t)及其一阶导数如下:
e(t)=q(t)-qd(t)(12)
式中,qd(t)是协作机器人关节角度的期望值;定义滑模面函数s(t)如下:
式中,
令
利用上一节设计的非线性扰动观测器对扰动量τdis(t,q)进行估计,观测器可设计如下:
式中,
对于补偿系统的不确定性及提高系统的鲁棒性,采用如下二阶滑模控制器:
τsosm(t)=m(q)·u(t)(18)
其中:
式中,k1,2,3,4>0,表示滑模控制增益;
基于非线性扰动观测器的有限时间跟踪控制器设计为:
t(t)=τeq(t)+τobs(t)+τsosm(t)(20)
针对式(2)所描述的协作机器人系统,在由等效控制器、非线性扰动观测器、和二阶滑模控制器所构成的有限时间跟踪控制器的作用下,得出如下结论:
1)协作机器人系统能够实现对关节期望轨迹的有效跟踪;
2)关节的跟踪误差能够在有限的时间内快速收敛至零;
3)控制力矩中的抖振能够被有效地抑制,同时该控制系统不会出现奇异性问题;
d.搭建协作机器人matlab/simulink仿真模型:
基于所述有限时间跟踪控制方法,在matlab/simulink环境中搭建协作机器人控制系统的仿真模型;该仿真模型主要包含四个主要模块,分别是输入模块、控制器模块、动力学模型模块和输出模块;其中,控制器模块包括等效控制器模块、非线性扰动观测器模块及二阶滑模控制器模块;
输入模块用于定义协作机器人的期望关节角度qd(t),;
滑模切换函数模块用于定义具有全局快速收敛特性的滑模切换面,滑模切换函数模块利用非奇异快速终端滑模切换函数结果输入等效控制器模块和二阶滑模控制器模块;
等效控制器模块、非线性扰动观测器模块及二阶滑模控制器模块组成总控制器,作为控制器模块用于控制协作机器人的轨迹跟踪运动;
动力学模型模块用于定义协作机器人的动力学模型;
输出模块用于输出协作机器人的期望关节角度或期望轨迹,从而输出期望轨迹,输出模块用于输出协作机器人的关节运动的实际轨迹;
e.仿真结果分析:
根据仿真结果,分别得到协作机器人关节的角度和角速度轨迹跟踪结果、角度和角速度的误差收敛情况以及非线性扰动观测器对干扰的逼近结果;具体包括关节角速和角速度的轨迹跟踪图、关节角度和角速度的误差收敛图、非线性扰动观测器对干扰的逼近结果图。
本发明与现有技术相比较,具有如下显而易见的突出实质性特点和显著优点:
1.本发明有限时间跟踪控制方法,用于解决协作机器人的轨迹跟踪控制问题;在控制系统中,利用非线性扰动观测器逼近控制系统中存在的集中扰动,并利用观测器的输出值对集中扰动进行补偿,进而削弱集中扰动对控制系统的影响;
2.本发明方法利用一种新型的非奇异快速终端滑模切换函数,设计了等效控制器,特点是收敛速度快、跟踪误差小且非奇异性;
3.本发明方法设计二阶滑模控制器,用于补偿非线性扰动观测器的跟踪误差,同时能够提高控制系统的稳定性和抗干扰能力。
附图说明
图1为本发明基于协作机器人有限时间跟踪控制的控制系统架构图。
图2为本发明基于协作机器人有限时间跟踪控制的控制系统matlab/simulink仿真图。
图3为本发明实施例二的协作机器人的关节角度跟踪轨迹。
图4为本发明实施例二的协作机器人的关节角速度跟踪轨迹。
图5为本发明实施例二的协作机器人关节角度和角速度的误差收敛情况。
图6为本发明实施例二的非线性扰动观测器对干扰的逼近结果。
具体实施方式
本发明的优选实施例结合附图详述如下:
实施例一:
参见图1-图2,一种基于有限时间跟踪控制的协作机器人控制方法,操作步骤如下:
a.建立协作机器人的动力学模型:
针对协作机器人,以关节为研究对象,利用拉格朗日法求解协作机器人的动力学模型,通过以下所示的二阶微分方程表示:
式中,
式中,τdis(t,q)定义为一个集中扰动向量,表达式如下所示:
式中,δm(q),
b.设计非线性扰动观测器:
记
式中,
定义辅助变量z如下:
式中,函数向量
结合式(4),对式(5)求导得:
令
将式(7)代入到式(6)中可得:
因此,非线性扰动观测器设计为:
其中:
式中,
c.设计协作机器人有限时间跟踪控制器:
定义协作机器人的关节角度误差函数e(t)及其一阶导数如下:
e(t)=q(t)-qd(t)(12)
式中,qd(t)是协作机器人关节角度的期望值;定义滑模面函数s(t)如下:
式中,
令
利用上一节设计的非线性扰动观测器对扰动量τdis(t,q)进行估计,观测器可设计如下:
式中,
对于补偿系统的不确定性及提高系统的鲁棒性,采用如下二阶滑模控制器:
τsosm(t)=m(q)·u(t)(18)
其中:
式中,k1,2,3,4>0,表示滑模控制增益;
基于非线性扰动观测器的有限时间跟踪控制器设计为:
t(t)=τeq(t)+τobs(t)+τsosm(t)(20)
针对式(2)所描述的协作机器人系统,在由等效控制器、非线性扰动观测器、和二阶滑模控制器所构成的有限时间跟踪控制器的作用下,得出如下结论:
1)协作机器人系统能够实现对关节期望轨迹的有效跟踪;
2)关节的跟踪误差能够在有限的时间内快速收敛至零;
3)控制力矩中的抖振能够被有效地抑制,同时该控制系统不会出现奇异性问题;
d.搭建协作机器人matlab/simulink仿真模型:
基于所述有限时间跟踪控制方法,在matlab/simulink环境中搭建协作机器人控制系统的仿真模型;该仿真模型主要包含四个主要模块,分别是输入模块1、控制器模块7、动力学模型模块8和输出模块9;其中,控制器模块7包括等效控制器模块4、非线性扰动观测器模块6及二阶滑模控制器模块5;
输入模块1用于定义协作机器人的期望关节角度qd(t),;
滑模切换函数模块3用于定义具有全局快速收敛特性的滑模切换面,滑模切换函数模块3利用非奇异快速终端滑模切换函数结果输入等效控制器模块4和二阶滑模控制器模块5;
等效控制器模块4、非线性扰动观测器模块6及二阶滑模控制器模块5组成总控制器,作为控制器模块7用于控制协作机器人的轨迹跟踪运动;
动力学模型模块8用于定义协作机器人的动力学模型;
输出模块1用于输出协作机器人的期望关节角度或期望轨迹,从而输出期望轨迹,输出模块9用于输出协作机器人的关节运动的实际轨迹;
e.仿真结果分析
根据仿真结果,分别得到协作机器人关节的角度和角速度轨迹跟踪结果、角度和角速度的误差收敛情况以及非线性扰动观测器对干扰的逼近结果;具体包括关节角速和角速度的轨迹跟踪图、关节角度和角速度的误差收敛图、非线性扰动观测器对干扰的逼近结果图。
本实施例有限时间跟踪控制方法,用于解决协作机器人的轨迹跟踪控制问题;在控制系统中,利用非线性扰动观测器逼近控制系统中存在的集中扰动,并利用观测器的输出值对集中扰动进行补偿,进而削弱集中扰动对控制系统的影响。本实施例利用非线性扰动观测器逼近并且补偿控制系统中存在的集中扰动量,利用非奇异快速终端滑模切换函数设计等效控制器,特点是收敛速度快及具有全局快速收敛特性。另外,本实施例方法设计二阶滑模控制器,用于补偿非线性扰动观测器的逼近误差,同时有助于增强控制系统的稳定性和抗干扰能力。
实施例二:
本实施例与实施例一基本相同,特别之处在于:
在本实施例中,参考图1~图6,基于有限时间跟踪控制的协作机器人控制方法,操作步骤如下:
a.建立协作机器人的动力学模型:
根据实施例一的步骤a,为了简化仿真模型,以二自由度协作机器人模型为例构建仿真控制系统,其动力学模型如下:
式中,q=[q1q2]t,q1,q2分别是协作机器人的关节运动角度。矩阵m(q),
式中,
b.设计非线性扰动观测器:
根据上述发明内容b的内容,非线性扰动观测器设计如下:
其中:
式中,x是一个常数可逆矩阵,取x=diag(0.0626,0.0626)。
c.设计协作机器人有限时间跟踪控制器:
根据上述发明内容c的内容,协作机器人有限时间跟踪控制器设计如下:
t(t)=τeq(t)+τobs(t)+τsosm(t)(28)
τsosm(t)=m(q)·u(t)(31)
其中:
式中,λ1=2,λ2=0·5,α=2,γ=7,ι=5,k1=5,k2=20,k3=3和k4=25。
d.搭建协作机器人matlab/simulink仿真模型:
根据上述发明内容d的内容,建立如图2所示的协作机器人有限时间跟踪控制系统的matlab/simulink仿真系统模型。
e.仿真结果分析
通过仿真结果得到协作机器人关节角度和角速度的轨迹跟踪情况及误差收敛情况、非线性扰动观测器对干扰的逼近结果。图1是协作机器人有限时间跟踪控制的控制系统架构,图2是协作机器人有限时间跟踪控制系统的matlab/simulink仿真系统模型,图3是协作机器人关节角速的轨迹跟踪情况,图4是协作机器人关节角速度的轨迹跟踪情况,图5是协作机器人关节角度和角速度的误差收敛情况,图6是非线性扰动观测器对干扰的逼近结果。角度的量纲是弧度(rad),角速度的量纲是弧度每秒(rad/s)。从图3和图4看出有限时间跟踪控制器能够实现对目标角度轨迹和角速度轨迹的有效跟踪。根据图5,关节的角度跟踪误差和角速度跟踪误差能够快速地收敛至零。在图5的局部放大图中,跟踪误差出现突变是因为集中扰动量中包含了不连续函数。事实上,干扰的形式是多种多样的,并且无法准确地预测,因此关节的跟踪误差不会总是趋于某个特定的值,甚至是零。控制器只能保证关节的跟踪误差在零的某一个很小的且可接受的邻域内波动。从图6得出非线性扰动观测器能够有效地对干扰进行补偿。根据仿真结果,对于给定的协作机器人系统,在有限时间控制器的作用下,协作机器人能够有效地跟踪目标轨迹,并且关节跟踪误差是最终一致有界的。
本实施例基于协作机器人有限时间跟踪控制方法,有效地提高协作机器人系统的稳定性及抗干扰能力,同时能够保证协作机器人的关节跟踪误差在有限的时间内收敛至零,对提高协作机器人的控制性能有重大的指导意义。
综上所述,上述实施例基于有限时间跟踪控制的协作机器人控制方法,应用于协作机器人控制系统设计领域,其操作步骤为:1)利用拉格朗日法建立协作机器人系统的动力学模型;2)设计非线性扰动观测器,用于补偿控制系统中存在的集中扰动量;3)设计有限时间控制器,用于协作机器人的轨迹跟踪控制;4)在matlab/simulink环境中搭建协作机器人有限时间跟踪控制系统的仿真模型;5)通过仿真实验,分析在有限时间跟踪控制器的作用下,协作机器人关节角度和角速度的轨迹跟踪情况及误差收敛性情况。上述实施例方法具有一定的创新性和可行性,可用于解决现有协作机器人控制系统中存在的跟踪误差收敛较大及抗干扰能力差等缺陷,对协作机器人控制系统的设计具有一定的借鉴意义。
上面对本发明实施例结合附图进行了说明,但本发明不限于上述实施例,还可以根据本发明的发明创造的目的做出多种变化,凡依据本发明技术方案的精神实质和原理下做的改变、修饰、替代、组合或简化,均应为等效的置换方式,只要符合本发明的发明目的,只要不背离本发明的技术原理和发明构思,都属于本发明的保护范围。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



