一种多重多维动力系统运动模型构建与模拟方法与流程

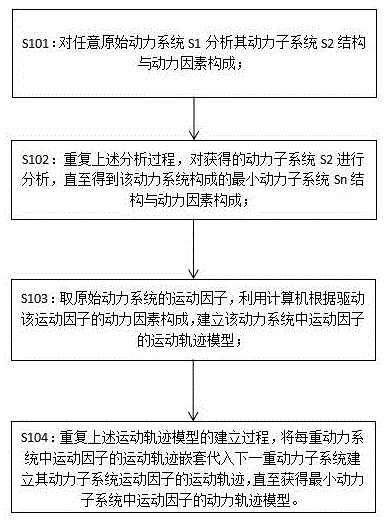
本发明涉及动力系统技术领域，尤其涉及一种多重多维动力系统运动模型构建与模拟方法。

背景技术：

在基础物理对微观量子效应和宏观宇宙的广义相对论进行解释的过程中，需要对微观量子与宏观宇宙中多运动因子的运动模型进行合理构建与模拟。

现有多重动力系统模型的构建，一般仅对微观中运动因子或仅对宏观中运动因子或某一类特殊运动的运动因子进行描述，构建过程通常通过获取运动轨迹并根据运动轨迹进行运动模型构建与模拟。其只适用于简单模型构建，若用该方法对多重/高重动力系统模型进行构建，模拟计算量巨大，对计算资源需求要求高；同时构建的运动模型不能对微观量子效应和宏观宇宙的广义相对论进行共同的解释。因此，如何提供一种多重多维动力系统运动模型及其快速构建与模拟方法，来统一微观粒子与宏观宇宙中运动因子的运动规律，是一个亟需解决的技术问题。

上述内容仅用于辅助理解本发明的技术方案，并不代表承认上述内容是现有技术。

技术实现要素：

本发明的主要目的在于提供一种多重多维动力系统运动模型构建与模拟方法，旨在解决现有技术中存在的多重动力系统模型的构建只适用于简单模型构建，同时构建的运动模型不能对微观量子效应和宏观宇宙的广义相对论进行共同的解释的技术问题。

为实现上述目的，本发明的第一方面，提供一种多重多维动力系统运动模型构建方法，所述多重多维动力系统运动模型构建方法包括如下步骤：

s101：对任意原始动力系统s1分析其动力子系统s2结构与动力因素构成；

s102：重复上述分析过程，对获得的动力子系统s2进行分析，直至得到该动力系统构成的最小动力子系统sn结构与动力因素构成；

s103：取原始动力系统的运动因子，利用计算机根据驱动该运动因子的动力因素构成，建立该动力系统中运动因子的运动轨迹模型；

s104：重复上述运动轨迹模型的建立过程，将每重动力系统中运动因子的运动轨迹嵌套代入下一重动力子系统建立其动力子系统运动因子的运动轨迹，直至获得最小动力子系统中运动因子的动力轨迹模型。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中：原始动力系统s1、动力子系统s2…动力子系统sn皆为球型系统。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中：动力因素包括该运动因子本身提供的动力因素和该运动因子在其动力系统下其它动力因子所提供的动力因素。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中，所述动力轨迹模型包括由球心center、法向normal、方向direction、半径radius构成的运动因子在其动力系统下的运动轨迹表达式：

sphere={center:(x,y,z),normal:(x,y,z),direction:(x,y,z):radiusout:number}；

其中，x、y、z分别为三维空间的坐标；number为半径预设值。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中，所述将每重动力系统中运动因子的运动轨迹嵌套代入下一重动力子系统建立其动力子系统运动因子的运动轨迹，包括如下步骤：

获取任意一重动力系统的运动轨迹表达式：

sphereout={centerout:(x,y,z),normalout:(x,y,z),directionout:(x,y,z):radiusout:number}；

centerin取在经过centerout方向为normalout的直线上；

radiusin取小于radiusout；

normalin与normalout呈预设夹角；

directionin为以其法向normalin为轴的预设方向；

根据获得的centerin、radiusin、normalin和directionin建立其动力子系统运动因子的运动轨迹表达式：

spherein={centerin:(x,y,z),normalin:(x,y,z),directionin:(x,y,z):radiusin:number}。

本发明的第二方面，提供一种多重多维动力系统运动模型模拟方法，所述多重多维动力系统运动模型模拟包括如下步骤：

s201：利用计算机模拟最小动力子系统sn中运动因子关于第1预设原点的动力轨迹模型；获取该最小动力子系统sn作为其上重动力子系统sn-1的运动因子关于第2预设原点的动力轨迹模型；

s202：重复上述模拟过程，获得最上重动力系统s1关于第n预设原点的动力轨迹模型；

s203：将获得的所有动力轨迹模型在三维空间进行展示得到多重多维动力系统运动模型。

优选的，一种多重多维动力系统运动模型模拟方法，所述所述多重多维动力系统运动模型构建过程中：最小动力子系统sn、其上重动力子系统sn-1…最上重动力系统s1皆为球型系统。

本发明中，通过对提出多重多维动力系统运动模型进行构建与模拟的过程，利用将每重动力系统中运动因子的运动轨迹嵌套代入下一重动力子系统建立其动力子系统运动因子的运动轨迹，直至获得最小动力子系统中运动因子的动力轨迹模型进行多重多维动力系统运动模型构建；利用计算机模拟最小动力子系统sn中运动因子关于第1预设原点的动力轨迹模型，获取该最小动力子系统sn作为其上重动力子系统sn-1的运动因子关于第2预设原点的动力轨迹模型；重复直至获得最上重动力系统s1关于第n预设原点的动力轨迹模型。旨在解决现有技术中存在的多重动力系统模型的构建只适用于简单模型构建，对多重/高重动力系统模型进行构建时，模拟计算量巨大，计算资源需求要求高；同时构建的运动模型不能对微观量子效应和宏观宇宙的广义相对论进行共同的解释的技术问题。基于构建与模拟的多重多维动力系统能够统一微观粒子与宏观宇宙中所有的运动因子的运动规律。对量子理论、时空弯曲及高维时空、多重宇宙、粒子物理模型、超弦理论提供合理的解释。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图示出的结构获得其他的附图。

图1为本实施例提出的多重多维动力系统运动模型构建方法的步骤流程示意图。

图2为本实施例提出的五重球型动力系统的实体静态模型一。

图3为本实施例提出的五重球型动力系统的实体静态模型二。

图4为本实施例提出的五重球型动力系统的实体动态模型。

图5为本实施例提出的计算机构建的五重球体旋转运动模型。

图6为本实施例提出的隐藏掉五重球体后的五重圆圈的旋转运动示意图。

图7为本实施例提出的五重圆圈旋转运动标注点的轨迹示意图。

图8为本实施例提出的五重球型动力系统的多种轨迹示意图。

图9为本实施例提出的多重多维动力系统的动力轨迹模型示意图。

图10为本实施例提出的多重多维动力系统运动模型构建与模拟方法的步骤流程示意图.

图11为本实施例提出的多重多维动力系统的动力轨迹数字实体模型示意图。

本发明目的的实现、功能特点及优点将结合实施例，参照附图做进一步说明。

具体实施方式

应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅是本发明的一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

本发明提出了一种实施例，参照图1，图1为本发明提出的一种多重多维动力系统运动模型构建方法的步骤流程示意图。

如图1所示，在本实施例中，一种多重多维动力系统运动模型构建方法，所述多重多维动力系统运动模型构建方法包括如下步骤：

s101：对任意原始动力系统s1分析其动力子系统s2结构与动力因素构成；s102：重复上述分析过程，对获得的动力子系统s2进行分析，直至得到该动力系统构成的最小动力子系统sn结构与动力因素构成；s103：取原始动力系统的运动因子，根据驱动该运动因子的动力因素构成，建立该动力系统中运动因子的运动轨迹模型；s104：重复上述运动轨迹模型的建立过程，将每重动力系统中运动因子的运动轨迹嵌套代入下一重动力子系统建立其动力子系统运动因子的运动轨迹，直至获得最小动力子系统中运动因子的动力轨迹模型。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中：原始动力系统s1、动力子系统s2…动力子系统sn皆为球型系统。

在本实施例中，如图2-4所示，为五重球型动力系统的实体模型。

在本实施例中，提供上述五重球型动力系统的构建：

建立一个五重球体的旋转模型。第一旋转球，半径为r1，周期为t1；第一旋转球中设置有第二旋转球，半径为r2，周期为t2；第二旋转球中设置有第三旋转球，半径为r3，周期为t3；第三旋转球中设置有第四旋转球，半径为r4，周期为t4；第四旋转球中设置有第五旋转球，半径为r5，周期为t5。五重球的球心没有重叠。五重球开始旋转运动时，相互之间的旋转轴方向有15至45度的差异。计算机构建的五重球体旋转运动模型如图5所示，当隐藏掉五重球体后的五重圆圈的旋转运动如图6所示，在五重圆圈上各标注一个点，五重圆圈旋转运动的五重轨迹如图7所示，多重动力系统旋转运动的多重轨迹见图8。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中：动力因素包括该运动因子本身提供的动力因素和该运动因子在其动力系统下其它动力因子所提供的动力因素。

优选的，如图9所示，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中，所述动力轨迹模型包括由球心center、法向normal、方向direction、半径radius构成的运动因子在其动力系统下的运动轨迹表达式：

sphere={center:(x,y,z),normal:(x,y,z),direction:(x,y,z):radiusout:number}；

其中，x、y、z分别为三维空间的坐标；number为半径预设值。

优选的，一种多重多维动力系统运动模型构建与模拟方法，所述多重多维动力系统运动模型构建过程中，所述将每重动力系统中运动因子的运动轨迹嵌套代入下一重动力子系统建立其动力子系统运动因子的运动轨迹，包括如下步骤：

获取任意一重动力系统的运动轨迹表达式：

sphereout={centerout:(x,y,z),normalout:(x,y,z),directionout:(x,y,z):radiusout:number}；

centerin取在经过centerout方向为normalout的直线上；

radiusin取小于radiusout；

normalin与normalout呈预设夹角；

directionin为以其法向normalin为轴的预设方向；

根据获得的centerin、radiusin、normalin和directionin建立其动力子系统运动因子的运动轨迹表达式：

spherein={centerin:(x,y,z),normalin:(x,y,z),directionin:(x,y,z):radiusin:number}。

如图10所示，本实施例提供的一种多重多维动力系统运动模型模拟方法的步骤流程示意图，所述多重多维动力系统运动模型模拟包括如下步骤：

s201：利用计算机模拟最小动力子系统sn中运动因子关于第1预设原点的动力轨迹模型；获取该最小动力子系统sn作为其上重动力子系统sn-1的运动因子关于第2预设原点的动力轨迹模型；

s202：重复上述模拟过程，获得最上重动力系统s1关于第n预设原点的动力轨迹模型；

s203：将获得的所有动力轨迹模型在三维空间进行展示得到多重多维动力系统运动模型。

优选的，一种多重多维动力系统运动模型模拟方法，所述所述多重多维动力系统运动模型构建过程中：最小动力子系统sn、其上重动力子系统sn-1…最上重动力系统s1皆为球型系统。

在该实施例中，提供一种多重多维动力系统运动模型模拟方法。

假设一个有n重的动力系统，最外重为1，最内（最小）重为n。数学描述中，以第1重旋转运动动力系统的中心为坐标原点，以旋转经过原点的平面为基础平面，基础平面上为x轴和y轴，z轴垂直于基础平面，xyz轴构成了多重多维动力系统的三维空间坐标系。每一重动力系统（ni）都以第ni重动力系统在ni-1重动力系统中的轨线为原点，其旋转面与第1重动力系统的基础平面的起始夹角（又叫倾角）为θi。第i重动力系统的旋转半径为其原点与第i+1重动力系统的原点的距离ri，第i重动力系统的旋转运动速度（或周期）为ti。由此得出五重动力系统的运动轨迹如图11。

第1重动力系统的运动轨迹就在xy且经过原点o的平面上，它的半径为r1，倾角为0，运行周期为t1。第1重动力系统的运动轨线为：ξ1（r1，θ1，t1ǀ0），即ξ1（r1，0，t1ǀ0）

第2重动力系统沿着第一重轨线旋转运动的同时，自身又进行旋转运动，其旋转面在起始时与xoy的倾角为θ2，旋转运动的半径为r2，旋转运动周期为t2，则第2重动力系统的运动轨线为：ξ2（r2，θ2，t2ǀξ1）。这样就将第1重动力系统和第2重动力系统的运动轨迹迭代合并到了第2重动力系统。

同理，第i重动力系统沿着第i-1重轨线进行旋转运动，其旋转面的半径为ri，旋转面在起始时与xoy的倾角为θi，旋转运动周期库ti，则第i重动力系统的运行轨线为：ξi（ri，θi，tiǀξi-1）。这里的ξi-1表示第i重动力系统的原点是在第i-1重动力系统运动轨线上旋转运动的。

在本实施例中，通过对提出多重多维动力系统运动模型进行构建与模拟的过程，利用将每重动力系统中运动因子的运动轨迹嵌套代入下一重动力子系统建立其动力子系统运动因子的运动轨迹，直至获得最小动力子系统中运动因子的动力轨迹模型进行多重多维动力系统运动模型构建；利用计算机模拟最小动力子系统sn中运动因子关于第1预设原点的动力轨迹模型，获取该最小动力子系统sn作为其上重动力子系统sn-1的运动因子关于第2预设原点的动力轨迹模型；重复直至获得最上重动力系统s1关于第n预设原点的动力轨迹模型。旨在解决现有技术中存在的多重动力系统模型的构建只适用于简单模型构建，同时构建的运动模型不能对微观量子效应和宏观宇宙的广义相对论进行共同的解释的技术问题。

基于上述构建与模拟的多重多维动力系统能够统一微观粒子与宏观宇宙中所有的运动因子的运动规律。对量子理论、时空弯曲及高维时空、多重宇宙、粒子物理模型、超弦理论进行令人信服的解释；其中：

(1)高维时空和多重宇宙。

用多重多维动力系统代替高维时空和多重宇宙，从多重动力系统来看，从银河系、太阳系、地球、原子、质子（中子）到基本粒子等都是不同层次的动力系统。如果将每重动力系统定义为1个时空维度，那么，从宏观到微观就构成了多重多维时空系统，也可称之为多重宇宙。由多重动力系统构成的时空维度就是超越了当前人们认识的四维时空之上的高维时空系统。那些超越四维时空系统的现象和难题在高维时空系统就能够得到科学的理解和阐释。

(2)时空弯曲在多重多维动力系统的中表现。

由于每一重时空维度（每一重旋转动力系统）都有不同的大小、不同的旋转运动方向、不同的运动时间（周期或频率），它们决定了不同的时空特性。因此，由不同重数的动力系统形成的时空具有不同的时空特性。不同的多重多维动力系统所形成的时空也具有不同的时空特性。这些不同特性的时空就是时空在宇宙中不同区域的差异，不同区域的时空差异就表现为时空的弯曲。辐射的光在宇宙中运行时，将通过许多不同的动力系统，也就是要通过许多不同特性的时空，当光线经过这些不同特性的时空时，将会受到其作用而产生不同的变化。例如光线经过一个强大的动力系统；光线经过水汽层；光线经过三棱镜等，都发生了不同的变化。当辐射能量，例如光经过若干重动力系统或者经过若干个动力系统时，每一重动力系统或者每一个动力系统都将对其产生作用并使其留下相应的痕迹。

(3)多重多维动力系统的多维时空特性。

从宏观方向看，日常事物是第一重动力系统，包括动物、植物、大气层、海洋等，例如大气层的运动变化表现出狂风大浪、阴晴雨雪等时空特性。地球自转是第二重动力系统，它的运动变化表现为24小时周期、白昼交替等时空特性。地球公转（即太阳系的旋转）为第三重动力系统，它的运动变化表现出365天周期和春夏秋冬四季交替等时空特性。太阳系在银河系中围绕银河系中心运动为第四重动力系统，它在银河系中的运动表现为2.26亿年周期和以数千万年为时段的气象变化等时空特性。银河系在星系群中的运动为第五重动力系统。

从微观方向，物体的分子是第一重动力系统。分子决定物体的基本性质，如物体的密度（比重）、硬度、温度，固体、液体、气体等不同状态，这些基本性质就是分子层次的时空特性。原子是第二重动力系统，它的运动变化表现出的周期性（元素周期表所列）特征就是原子层次的时空特性。质子、中子等亚原子粒子是第三重动力系统，它们的运动周期、运动方式等就是亚原子层次的时空特性。电子、夸克、玻色子等是第四重动力系统，它们的运动周期、运动方式（如量子(quantum)特性）就是基本粒子的时空特性。构成基本粒子的能量子（energieelement）是第五重动力系统。

(4)量子效应是多重多维动力系统的基本规律。

量子运动的测不准（表现为随机性、叠加性）是量子在多重多维动力系统中运动的本质特性。量子之上有多重动力系统，由于每重动力系统具有不同的时空特性（大小、方向、周期），而量子的运动都遵从其上的各重动力系统的运动特性（规律）。由于量子同时具有多重动力系统的运动特性（大小、方向、周期），所以，量子的运动轨迹必然是其所在的多重动力系统运动轨迹的迭加合并而成。虽然每一重动力系统的运动轨迹（特性）是确定可测的，但是将多重动力系统的运动合并起来，就不具备确定的可测性了。也就是说，从多重动力系统外去观测量子在某一时刻的运动方向及位置和速度是不可能的。从不同重动力系统去测量或预测量子的运动，也必然会得出不同的结果。因此，量子运动的测不准、随机性和叠加态是多重多维动力系统运行规律赋予的本质属性。描述量子的运动应该沿着多重动力系统的运动迭加（迭代）去实现，才能揭示其真实过程。事实上，如果从星系群外观测地球上每一个人的运动，也是呈现出量子状态的。量子效应之所以不能被理解是因为我们现在只是从一重动力系统的四维时空（即地球及其四维时空）去观测多重动力系统中的微观粒子的运动过程，而不是从多重动力系统的迭代中观测量子行为。这犹如只从二维空间去观测，是不可能理解三维空间的现象一样。该实施例提供的多重多维动力系统构建与模拟方法解决了同一个物体或者同一个质点实现同时向多个或者n个方向运动的“奇异”现象和过程。

(5)亚原子粒子的波粒二象性是多重多维动力系统周期性旋转运动决定的基本属性。

微观粒子在多重多维动力系统中的运动具有多重动力系统的周期性旋转运动特性，它的运动本质上就具有周期性和波动性。微观粒子的波粒二象性可以概括为：第一，微观粒子单个粒子具有粒子性，它的运动轨线是波动性的；第二，微观粒子单独运行表现为粒子，但群体运行效应表现为波动性。简言之，微观粒子单个是粒子，群体是波。

(6)化学键。同一个多重多维动力系统的原子之间在涡漩运动中相互作用，它们在旋转运动的惯性力作用下相互靠近，同时它们之间的涡漩能量子和电子及其他辐射粒子也相互作用从而产生阻碍其靠近的阻力。趋近力和阻力相互缠绕形成扭合力，这种扭合力使原子之间相互结合，这就是化学键的本质。

(7)暗物质和暗能量。当物体的温度降到0k时，质子、中子、原子等涡漩周围的能量粒子几乎被驱散，它们之间会实现更紧密的结合，这时物体的物质密度会增加，同时又几乎不向外辐射能量，因而远距离就不能观测到它们的存在。暗物质就是不产生辐射的物体，暗物质也是暗能量的存在方式。能量子不发生辐射时，宇宙中看不见的能量子也是暗物质和暗能量的存在方式。宇宙万物在多重多维惯性系统中运行，宇宙万物的运动变化及相互作用都由不同层次的惯性力来驱动和维持，并不需要暗物质或暗能量来驱使或维持。

(8)质量。物体的质量本质上是物体所含能量子的数量。在同一个动力系统也是同一个惯性运动系统中，两个物体的质量大小可以用惯性质量来测度和比较。日常生活和科学研究中，都是用惯性质量代替物体的质量。物体的静止质量、运动质量和相对论质量（总质量）等也都是物体质量的不同表现形式。引力质量实质上是惯性质量。由于任何物体都由能量子构成，所以任何物体都具有质量。

在本实施例中，通过模拟与构建的多重多维动力系统运动模型能够解决现有技术中构建的运动模型不能对微观量子效应和宏观宇宙的广义相对论进行共同的解释的技术问题。其构建的多重多维动力系统运动模型能够在物理领域的实际应用及商业价值上起到好的效果：

（1）多重多维动力系统模型对物理研究和理论物理的创新发展具有重要的参考价值。

（2）多重多维动力系统模型对于从事物理研究及对物理乃至对自然科学感兴趣和有爱好的读者具有启迪和欣赏价值。

（3）将多重多维动力系统模型作为一种体验项目，可以让人们到多重多维动力系统中亲身体验高维时空的奇妙运行过程，具有较高的娱乐及商业运用价值。

（4）统一微观粒子与宏观宇宙中运动因子的运动规律。

以上所述仅是本发明的优选实施方式，应当理解本发明并非局限于本文所披露的形式，不应看作是对其他实施例的排除，而可用于各种其他组合、修改和环境，并能够在本文所述构想范围内，通过上述教导或相关领域的技术或知识进行改动。而本领域人员所进行的改动和变化不脱离本发明的精神和范围，则都应在本发明所附权利要求的保护范围内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除