一种预测定向凝固包晶合金糊状区内雀斑形貌缺陷的方法与流程

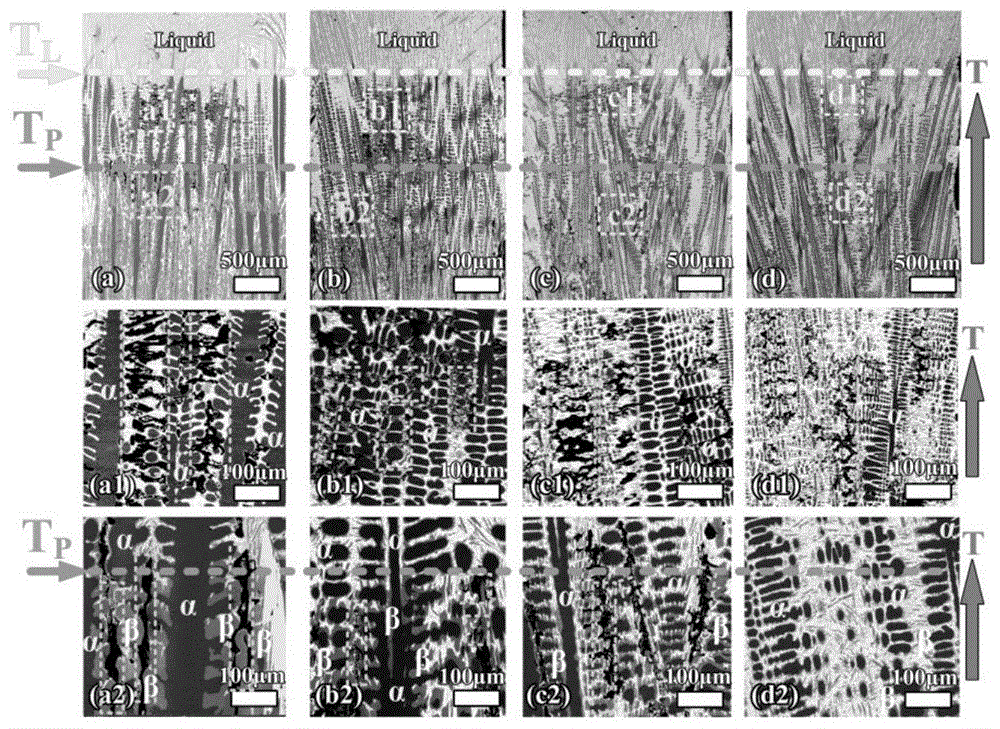
本发明涉及合金制备，具体为一种预测定向凝固包晶合金糊状区内雀斑形貌缺陷的方法。

背景技术：

在具有一定凝固区间的合金凝固过程中，会形成固液共存的糊状区。业已证明，糊状区中由于存在热对流，经常会形成雀斑形貌等缺陷。雀斑形貌由细小的枝晶碎片链和沿凝固方向的气孔组成，其存在严重影响了凝固材料的性能。在向上定向凝固过程中，假设温度分布稳定，热对流受到抑制，而当被排斥的溶质使熔体密度变轻时，溶质分布就不稳定，从而导致热对流。

为了量化树枝状糊状区中的纵向热对流，业已证明糊状区的雷诺数ra是预测雀斑形貌形成的有用参数。ra有几种定义，如果ra超过临界值，热对流开始，这会导致雀斑形貌的形成。ra直接受渗透率k的影响，而在常见的树枝状结构中渗透率k与枝晶臂的间距、固体的体积分数(fs)和枝晶的比表面积有关。因此，应合理地描述树枝状结构对ra的影响。

在枝晶凝固过程中，由吉布斯-汤姆逊(g-t)效应驱动的枝晶粗化导致了溶质在液体中以不同的半径在相邻的二次枝晶之间扩散，从而导致较细二次枝晶上发生重熔并在较粗二次枝晶上重新凝固。另外，熔体中的溶质扩散也可以由凝固过程中温度梯度所导致的溶质浓度梯度引起，这就是温度梯度区熔效应(tgzm)。在过去的几十年中，已经在fe-ni和钢合金等众多重要的包晶合金中观察到了枝晶生长。业已证明，包晶反应会限制枝晶粗化过程并促进tgzm效应。然而，目前对包晶凝固过程中与流体流动有关的树枝状糊状区的演变的分析还远远不够。

如上所述，尽管预测雀斑形貌形成非常重要，其关乎凝固制备的合金材料最终性能表现，但可用于预测雀斑形貌形成的数据相对较少，特别是针对包晶合金，预测的准确度较低。

技术实现要素：

针对现有技术中存在的问题，本发明提供一种预测定向凝固包晶合金糊状区内雀斑形貌缺陷的方法，在包晶凝固过程中，能够更准确得预测树枝状糊状区中雀斑形貌的形成。

本发明是通过以下技术方案来实现：

一种预测定向凝固包晶合金糊状区内雀斑形貌缺陷的方法，获取雷诺数与渗透率k的关系；

建立一种较细二次枝晶位于两个较粗二次枝晶之间的模型，并综合tgzm效应和g-t效应对二次枝晶的影响，获取渗透率k与糊状区内固相体积分数fs的关系；

根据上述各关系，得到雷诺数与固相体积分数fs的关系，通过雷诺数随固相体积分数fs变化时的最大值来预测缺陷的形成。

优选的，雷诺数与渗透率k的关系为：

(δρ/ρ0)＝ρ0-ρ(h)/ρ0(2)

其中，(δρ/ρ0)是糊状区中的液体密度的倒数，g是重力加速度，α是热扩散率，ν是动力学粘度，ρ0是在淬火固/液界面上方的熔体密度，ρ(h)是熔体的密度随高度的函数。

进一步的，渗透率k与固相体积分数fs的关系为：

其中，kc是kozeny-carman常数，sv是枝晶比表面积。

进一步的，枝晶比表面积sv为

其中，a和b分别是较粗二次枝晶臂和较细二次枝晶臂的长度，r为较细二次枝晶臂的半径，r为较粗二次枝晶臂的半径。

优选的，所述包晶合金为sn-36at.％ni合金。

优选的，雷诺数随固相体积分数fs变化时的最大值有两个，一个最大值位于包晶反应之前，另一个最大值位于包晶反应之后，两个最大值分别对应一雀斑形貌缺陷。

与现有技术相比，本发明具有以下有益的技术效果：

包晶凝固广泛存在于许多结构和功能材料中。如常见的不锈钢，磁性材料，或是永磁合金材料，高温超导材料，航空航天材料等的制备过程都和包晶反应息息相关。而包晶凝固过程中会形成固液共存的糊状区，糊状区中由于存在热对流，经常会形成雀斑形貌等缺陷。雀斑形貌由细小的枝晶碎片链和沿凝固方向的气孔组成，其存在严重影响了凝固材料的性能，但目前依然缺乏关于包晶凝固过程中雀斑形貌形成的研究报道。在不同生长速度下的定向凝固过程中，针对sn-36at.％ni包晶合金的树枝状糊状区的观察表明，雀斑形貌形成的区域可分两种：一是包晶反应之前的区域(区域一)，二是包晶反应之后的区域(区域二)，在生长速度较低时，雀斑形貌更多。而之前研究报道的雷诺数ra只能预测区域一雀斑形貌的形成，目前对区域二中雀斑形貌的形成还没有任何相关内容发表，也没有相应成果转化。对实验结果的检验表明，温度梯度区熔(tgzm)和吉布斯-汤姆逊(g-t)效应均对定向凝固过程中的树枝状形貌有明显影响。关于雷诺数ra的理论描述了树枝状糊状区的热溶质对流，通过ra的最大值来预测雀斑形貌的形成，这只能解释区域一中的雀斑形貌，却不能预测区域二中雀斑形貌的出现。因此，考虑到树枝状糊状区的作用和包晶反应，提出了一种新雷诺数rap。rap的理论预测除在包晶反应之前外也可以显示出包晶反应之后的最大值，因此，与区域二的雀斑形貌形成非常吻合，本发明的新雷诺数rap能够对区域二也作出解释。另外在生长速度较低时，新雷诺数rap可预测剧烈的热对流，这进一步证明了用rap描述雀斑形貌形成与生长速度的关系是十分可靠的。因此，本发明对包晶凝固过程雀斑形貌形成的预测更加全面，有利于减少最终包晶合金材料中的气孔等缺陷，从而大幅提高材料的可靠性及其他性能。因此，基于描述了两个因素的渗透率k的分析模型，提出了基于sn-ni包晶体系的定向凝固包晶合金中树枝状糊状区的新雷诺数rap。本发明新的雷诺数rap，在包晶凝固过程中，它能够更准确得预测树枝状糊状区中雀斑形貌的形成。

附图说明

图1是定向凝固sn-36at.％ni包晶合金树枝状糊状区雀斑形貌形成的典型微观结构：(a)5μm/s，(b)10μm/s，(c)20μm/s，(d)40μm/s，(a1)-(d1)显示了从tl到tp的区域一中的雀斑形貌的形成，(a2)-(d2)显示了低于包晶温度tp的区域二中的雀斑形成；

图2是不同生长速度下定向凝固的sn-36at.％ni包晶合金糊状区的宏观偏析：(a)溶质浓度与固相体积分数的关系；(b)log(cl/c0)与log(1-fs)的关系；(c)糊状区雷诺数ram，ray和ram的计算结果对比，此处以5μm/s为例进行计算。

图3是包晶合金定向凝固过程中tgzm和g-t效应对重熔/再凝固过程影响的对比图：(a)i，(b)ii，(c)iii，(d)iv。

图4是本发明提出的糊状区雷诺数rap与糊状区固相体积分数fs的关系：(a)5μm/s，(b)10μm/s，(c)20μm/s和(d)40μm/s，其中f为包晶反应常数，代表包晶反应的程度，以sn-ni包晶体系为例，f＝0代表无反应，f＝1.23代表完全反应，0<f<1.23则代表部分反应。

图5是考虑到tgzm效应时，不同生长速度下定向凝固sn-36at.％ni包晶合金中渗透率k的理论预测与实验结果的比较：(a)5μm/s，(b)10μm/s，(c)20μm/s和(d)40μm/s。

具体实施方式

下面结合具体的实施例对本发明做进一步的详细说明，所述是对本发明的解释而不是限定。

本发明需要先进行定向凝固实验制备样品棒，包括以下步骤：

首先用纯度为99.9％的镍和锡在感应熔炼炉中铸造sn-36at.％ni合金。然后从铸锭上切下直径为3mm，长度为110mm的棒。随后将棒放入al2o3管中并放入bridgman型炉。其次，将棒的温度升至1250℃使其熔化，后将样品在bridgman型炉中静置30分钟。随后在恒定的温度梯度下以不同的生长速度进行定向生长：5μm/s，10μm/s，20μm/s和40μm/s。之后当生长距离达到40mm时，将管快速淬火。最后将样品纵向切开，抛光后通过扫描电子显微镜(sem(quanta-200))分析棒的纵向截面的微观结构。由于样品在具有固定温度梯度的温度场中固化并随后淬火，因此可以首先确定液相从熔体中凝固的液相线温度tl。达到包晶反应开始的包晶反应温度tp时，在定向凝固的样品中可以发现包覆初生相二次枝晶的包晶相。通过将ptrh30-ptrh6热电偶放在定向坩埚样品固/液界面附近的氧化铝坩埚中，即可测量得到本实施例的温度梯度(g)。这些热电偶测得的温度分别表示为t1和t2，两个热电偶之间沿定向凝固方向的距离l为2mm。当样品以特定的凝固速度下拉时，借助于连接到计算机的数据记录器记录t1和t2。通过这种方式，可以测量定向凝固实验中t1和t2的关系，并确定温度梯度g＝(t1-t2)/l。

图1显示了四种不同生长速度下的典型树枝状结构。图1(a)-(d)显示了从1040℃(tl)的淬灭固/液界面到798℃(tp)的包晶反应界面的微观结构。eds结果表明深灰色相为ni3sn2相，浅灰色相为ni3sn4相，白色相为剩余液相。在这里，α和β分别代表初生ni3sn2相和包晶ni3sn4相。雀斑形貌由孔隙率、沿着凝固方向的等轴晶粒链或枝晶碎片组成。在这项工作中，黑色缺陷是枝晶间区域的孔隙率。由于可以从这些宏观视图中发现由等轴晶和孔隙率组成的线缺陷，因此可以断定该线缺陷是定向凝固过程中形成的雀斑形貌。此外，与以前的其他合金方法不同，雀斑形貌可以在两个不同的区域看到：tl和tp之间即包晶反应之前(区域一)和tp以下即包晶反应之后(区域二)。为了更好地显示这两个不同位置的雀斑形貌形态，图1(a1)-(d1)显示了区域一的微观结构，而在区域二中则观察到了接近包晶界面的微观结构图1(a2)-(d2)。

因为雀斑形貌由孔隙率、沿着凝固方向的等轴晶粒链或枝晶碎片组成，所以微孔的积累和生长可以直接影响雀斑形貌的形成。而微孔受枝晶间区域的热对流的影响会发生移动。在较低的生长速度下，较大的一次枝晶间距会导致更严重的热对流，因此，在枝晶间热对流更剧烈之处会聚集并产生更多微孔。因此，雀斑形貌形成的位置也是微孔聚集和产生较为明显的位置。此外，对图1(a2)-(d2)的检查表明，在较大的生长速度下可以发现较少的雀斑形貌。此外，可以找到具有不同半径的粗/细的二次枝晶，这印证了g-t效应的影响。此外，图1(a2)-(d2)还表明，包晶ni3sn4相仅在二次枝晶的前边缘包覆初生ni3sn2相，这也是包晶凝固过程中tgzm效应的典型形貌特征。而本发明阐明了这些作用如何影响树枝状形貌以及雀斑形貌的形成。

凝固过程中溶质不断被排入熔体再加上热对流的影响导致了溶质的重新分布，此时糊状区中发生溶质的宏观偏析。在图2(a)中给出了在这些样品中以不同的生长速度测得的纵向宏观偏析。从图2(a)可以看出，在相同比例的固相(初生ni3sn2相/包晶ni3sn4相)中，当生长速度较低时，熔质浓度较高。这表明纵向宏观偏析在较低的生长速度下更为明显。此外，在糊状区中存在热对流的情况下，实际溶质分配系数也会发生变化。由于随定向凝固的进行溶质浓度不断变化，因此在此绘制了log(cl/c0)与log(1-fs)的关系图(图2(b))。经过线性拟合，该关系可表达为宏观偏析数据表明，在较低的生长速度下，ke较小，此时热对流的影响更大。c0是合金初始成分，cl是溶质浓度，fs是固相体积分数，ke是平衡溶质分配系数。

尽管用雷诺数ra预测雀斑形貌的形成比较可靠，但不同出版物对其的表达各不相同，这使得对其的分析更加复杂。而beckermann等人指出的以下定义能更有效地预测雀斑形貌的形成：

(δρρ0)＝ρ0-ρ(h)/ρ0(2)

其中，(δρ/ρ0)是糊状区中的液体密度的倒数，g是重力加速度，α是热扩散率，ν是动力学粘度，tewari等人计算得出α和ν的积是4×10^-12m⁴/s²，ρ0是在淬火固/液界面上方的熔体密度，ρ(h)是熔体的密度随高度的函数，k是渗透率。关于渗透率k，他们假设：

kb＝6×10^-4(λ1/fs)²×(1-fs)³(3)

杨万宏等人认为k可以计算为：

之后，考虑二次枝晶对渗透率的影响，tewari和tiwari提出：

此处dl是熔体中的溶质扩散系数，g是糊状区中的温度梯度，v是生长速度，ml是固相的液相线斜率，c0是合金初始成分，k是溶质分配系数，λ1是一次枝晶间距。通过等式(3)-(6)，将获得的雷诺数分别定义为rab，ray和ram。

在图2(c)中，fs在0.01到0.9的范围内且v＝5μm/s时，分别进行了雷诺数这三个定义的预测，并且通过scheil方程，fs与溶质浓度cl有关。可以在所有三个预测中观察到最大值，并且当fs为0.51时，糊状区雷诺数ra的“突然”下降意味着包晶反应的发生。因为渗透率降低而糊状区中的液体密度的倒数项随fs增加，所以雷诺数会出现一个最大值。如果雷诺数ra超过临界值，则由于热对流而形成雀斑形貌，因此当雷诺数ra接近其最大值时会形成雀斑形貌。然而，根据图1中的实验结果，在两个不同的区域观察到了雀斑形貌，这表明在定向凝固过程中应该存在两个局部最大的雷诺数。但是，这不能通过当前的ra定义来预测。因此，在本发明工作中将开发ra的新定义以解决该问题。

由于糊状区的定义的区别，业已证明雷诺数可以由式(1)确定，本发明中糊状区雷诺数的新表达也应与之相符。对式(1)的研究表明，雷诺数的进一步研究只能通过特定合金体系糊状区的渗透率k来实现。因此，将首先分析在包晶凝固期间给定温度梯度时糊状区中树枝状结构的演变，从而确定渗透率k。

由于两种效应在树枝状结构演化过程中都起着重要作用，因此应首先阐明它们之间的相对重要性。为了与先前的粗化模型进行比较，如图3所示，这里建立了一种较细(半径为r)的二次枝晶位于两个较粗(半径为r>r)的二次枝晶之间的模型。因为这两种效应对较细二次枝晶的影响一般不同，所以较粗和较细二次枝晶的这种分布是合理的。tgzm效应导致后边缘/前边缘的重熔/凝固。然而，由g-t效应引起的重熔发生在较细二次枝晶的两个边缘。因此，该模型是合适的。此外，假定由这两种作用引起的溶质通量是独立的。

根据实验结果，如图3所示，在实验检查的基础上，整个过程可以分为四个阶段。在图3(a)中，只有α相参与了包晶反应发生前的阶段i。图3(a)中的三条倾斜直线是α相的液相线，其中黑色倾斜直线e为平衡液相线，其他两条是半径为r、r2时的液相线。图3(a)清楚地表明，在tr1和tr2处，tgzm效应引起的熔质浓度差δct大于g-t效应引起的熔质浓度差δcg。这表明在枝晶的上下边缘上，与tgzm效应相比，由g-t效应引起的重熔/凝固较弱。实际上，枝晶的上边缘的实际δc1是tr1处由两个效应引起的δc之差。同时，枝晶的下边缘上的实际δc2是tr2处两个效应的δc之和。因此，tr2的实际δc大于tr1的实际δc。

阶段ii起始于包晶反应发生之时，只有β相参与阶段ii。图3(b)说明了在tr1和tr2处，由g-t效应引起的溶质浓度差δcg仍小于由tgzm效应引起的溶质浓度差δct。tr2的重熔速度大于tr1的重熔速度。此外，tr2的β相应首先完全重熔，然后如图3(c)所示，进行阶段iii。在这种情况下，包晶β相出现在t2′，初生α相出现在tr2。图3(c)中的虚线是包晶反应后(tp下方)的α相的液相线，并假定它们是包晶反应前(tp上方)的斜直线的延长线。如上所述，tr2处的重熔速度大于tr1处的重熔速度，如图3(c)所示，阶段iii时，在t1′处的β相完全熔化。此时如图3(d)所示，β相出现在t1′，而初生α相出现在tr2。较细的二次枝晶臂消失时，该过程完成。

根据carman-kozeny模型，糊状区渗透率k表示为：

其中kc是kozeny-carman常数，在先前的工作中，将kc选择为3.0或5.0。在这项工作中发现，当kc为3.0时，理论预测与使用carman-kozeny模型的实验结果非常吻合。

根据本发明图3建立的模型，得到枝晶的比表面积sv为：

其中a和b分别是较粗二次枝晶臂和较细二次枝晶臂的长度。用a和b的平均测量值作为其初始值。

基于渗透率k的理论预测，给出了糊状区雷诺数与固相体积分数fs的关系。为了区别于先前的雷诺数，本发明中的新雷诺数这里写为rap。rap随生长速度的增加而降低，这是因为在生长速率较低时，一次枝晶间距较大而且二次枝晶还没形成，枝晶间热对流更强。如图4所示，目前新雷诺数rap的特殊之处是可以发现两个最大值：一个最大值在包晶反应之前，另一个在包晶反应之后。此外，尽管第一个最大值始终大于第二个最大值，但两个最大值都随生长速度的增加而减小，而第二个最大值在40μm/s的生长速度下几乎消失了。这里给出了第二最大值的放大图，以更好地理解包晶反应后rap的变化。如果雷诺数达到最大值，雀斑形貌就很可能会形成。由此本发明认为雀斑形貌形成的两个不同区域对应于rap的两个最大值。

值得注意的是，尽管第二个最大值始终小于第一个最大值，但仍可以在tp以下找到雀斑形貌。这表明雀斑形貌的形成不仅取决于雷诺数的绝对量，而且还取决于雷诺数的相对量。应该注意的是在这两个不同区域的雀斑形貌形成机理是不同的。对于包晶反应之前的区域一，因为渗透率降低，而液体密度的倒数随fs升高而升高，所以出现了最大值。对于包晶反应后的区域二，最大值的存在可以归因于包晶凝固过程中g-t和tgzm效应的综合影响，渗透率k明显增加(图5)。因此本发明认为在定向凝固期间，特别是在包晶反应之后，在糊状区内树枝状结构的渗透率发生变化，因此树枝状结构的细节可以显著地影响雷诺数rap，从而影响雀斑形貌的形成，也影响了材料的最终性能。

本发明通过如上方法能够预测雀斑形貌的形成，在实际工作中，为更便捷地实现对雀斑形貌形成的避免，本发明引入了固相体积分数fs与糊状区内的局部凝固时间tf的关系，如下所示。通过调节tf以调节fs，从而实现对雀斑形貌形成的避免。

a2＝2gyml(k-1)(12)

其中，fo是溶质扩散傅里叶数，c0是合金初始浓度，y是施加温度梯度的方向上枝晶内侧间距的一半，k是溶质分配系数，ds是固相的溶质扩散系数，λ2是二次枝晶间距，tf是糊状区内的局部凝固时间。d是液相的溶质扩散系数。

下面本发明将从四个方面阐述本发明的优势：

1.与其他类型的合金不同，在包晶合金定向凝固过程中，在两个不同的区域形成雀斑形貌：包晶反应之前的区域一和包晶反应之后的区域二。当前关于雷诺数ra的理论仅能解释区域一，其通过ra的最大值预测雀斑形貌的形成，而本发明的新雷诺数rap能够对区域二也作出解释。

2.在定向凝固的sn-ni包晶合金中，在施加温度梯度的条件下，本发明阐述了tgzm和g-t效应对糊状区树枝状结构演化的影响。

3.建立了基于carman-kozeny方程的分析模型，描述了包晶合金定向凝固过程中糊状区树枝状结构的流体渗透率k。另外在包晶反应后发现k的升高，本发明认为这是由包晶凝固过程中tgzm和g-t效应的综合影响引起的重熔/再凝固过程引起的。

4.基于k的预测，本发明提出了定向凝固过程中树枝状糊状区的新雷诺数rap，其在包晶反应前后均表现出两个最大值，因此与不同区域的雀斑形貌形成非常吻合。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除