一种基于孟德尔随机化的多性状全转录组关联分析方法、系统及其应用与流程
 2021-01-08 11:01:24|
2021-01-08 11:01:24| 373|
373| 起点商标网
起点商标网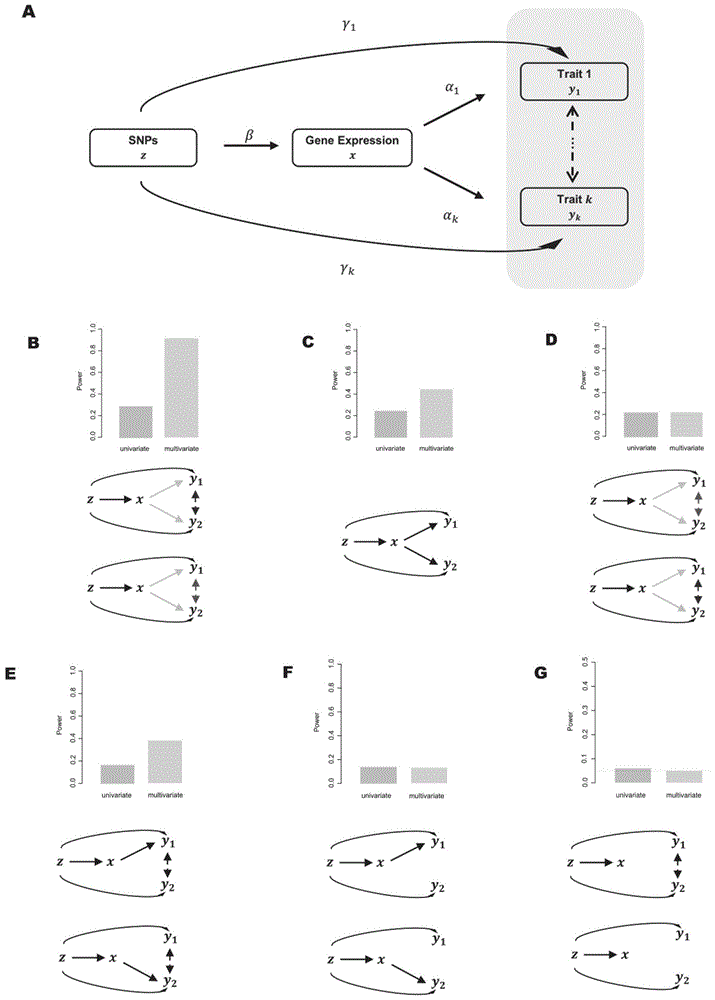
本发明属于生物技术和数据分析技术领域,具体涉及一种基于孟德尔随机化的多性状全转录组关联分析方法及其应用。
背景技术:
公开该背景技术部分的信息仅仅旨在增加对本发明的总体背景的理解,而不必然被视为承认或以任何形式暗示该信息构成已经成为本领域一般技术人员所公知的现有技术。
全转录组关联研究(transcriptome-wideassociationstudy,twas)在设计上旨在整合全基因组关联研究(genome-wideassociationstudies,gwass)和基因表达谱研究,以探讨复杂疾病的内在分子遗传机制。twas将特定基因的顺式snps(cis-snps)作为工具变量,进而检验该特定基因与gwas性状的因果效应,因此,twas的分析策略可以纳入孟德尔随机化(mendelianrandomization,mr)框架。目前已产生了许多twas统计分析方法,包括predixcan,twas,dpr,tigar,smr,pmr-egger,focus和utmost等。不同的twas方法在以下诸多方面存在差异:纳入分析的cis-snps数目不同(有些方法使用一个cis-snp,而有些方法使用所有cis-snps);是否校正了水平基因多效性(有些方法考虑了水平多效性,而有些方法未考虑);构建的cis-snps对基因表达的预测模型假设不同(有些方法依赖于稀疏性假设,而有些方法依赖于基因多效性假设);模型推断方式不同(有些方法基于似然进行推断,而有些方法基于两阶段回归策略进行推断)。
尽管当前twas分析方法众多,但在本质上都是针对单性状进行分析。然而,gwas研究通常包含具有共同遗传基础的多个相关性状,许多位点已经被证实与多种表型之间存在多效关联,比如,cacna1c与双相情感障碍和精神分裂症、slc39a8与精神分裂症和帕金森病、rgs12与血脂和炎症性肠病。因此,对多个性状的联合分析势必能够提升twas的检验效能。事实上,多性状联合分析优于单性状分析已在gwas中得到了证明。在识别同时影响多个性状的基因时,多性状联合twas分析比单性状twas具有更高的检验效能。此外,将多性状间的相关性考虑在内,多性状联合分析也比单性状分析能够更有效地识别只影响其中一个性状的基因。因此,发展多性状联合的twas统计分析方法势在必行。
技术实现要素:
针对上述现有技术的不足,本发明提供一种基于孟德尔随机化的多性状全转录组关联分析方法、系统及其应用。基于先前twas分析的似然推断框架,将其拓展到多个结局性状,提出了一种新型的多性状twas方法。该方法考虑了多个性状之间的相关性,适用于存在高度连锁不平衡(linkagedisequilibrium,ld)的cis-snps,借助广泛使用的egger假设将水平基因多效性嵌入模型,并且基于极大似然理论进行推断,本发明将其命名为具有egger假设的多结局概率孟德尔随机化(mopmr-egger)方法。模拟和实例分析表明,mopmr-egger在检验因果效应和水平多效性时可以控制一类错误,比单性状方法具有更高的检验效能,并且可以用于生物库规模数据的实证分析,计算效率高,因此具有良好的实际应用之价值。
本发明是通过如下技术方案实现的:
本发明的第一个方面,提供一种基于孟德尔随机化的多性状全转录组关联分析方法,所述分析方法包括依托两样本mr框架,在没有样本重叠的两项独立研究中测量暴露和结局,从而估计和检验暴露对结局的因果效应;具体的,一次检验一个基因,并将cis-snps作为工具变量,在似然框架下同时估计和检验基因对多个结局性状的因果效应,同时能将潜在的水平多效性嵌入模型。
所述分析方法包括对个体水平数据进行分析和汇总统计量数据进行分析。
其中,当对个体水平数据进行分析时,所述分析方法包括采用如下回归模型:
尽管上述三个公式针对的是两个独立的研究,但参数β将二者紧密的结合起来。式(2)-(3)可以合并为
其中,
遵循遗传学中常用的多基因建模假设,假设β的所有元素非零,且每个元素都服从正态分布
在上述联合模型中,所关心的参数是基因在多个结局性状上的因果效应α。α的因果效应识别和可解释性可以基于因果推断中的决策理论加以证明。和传统的mr分析一样,α的因果解释至少需要两个假设成立:(1)工具变量与基因表达有关;(2)工具变量与基因表达和每个结局都有关的任何其他混杂因素无关。因为对水平多效性γ做了明确的模型假设,mopmr-egger不再要求满足mr的一般排除限制条件(即,工具变量只能通过基因表达途径影响每个结局)。然而,对γ的模型假设需要满足工具变量强度与直接效应独立的假设(instrumentstrengthindependentofdirecteffect,inside),这个假设要求工具变量-基因表达效应和工具变量-结局效应是相互独立的,有时称为弱排除限制条件。因为混杂因素往往是未知的,这些假设有许多在实践中是无法检验的,本发明所使用的术语“因果效应”,只是为了强调α的估计比y对
在上述模型中,感兴趣的是在水平多效性γ存在时,估计因果效应α并检验原假设h0:α=0,拒绝原假设α=0意味着基因表达至少对一个性状有非零的因果效应。另外,还可对水平多效性γ进行估计和检验h0:γ=0,拒绝原假设γ=0说明cis-snps至少对一个性状有非零的水平多效性。在统计推断层面,发展了期望最大化(em)算法的参数扩展版本(px-em),通过最大化基于式(1)和(4)定义的联合似然来进行参数推断。可以获得最大似然联合模型以及α和γ最大似然估计。此外,进一步将该em算法应用于两个简化模型,一个模型中不包含α,另一个模型中不包含γ,分别获得对应的最大似然。最后,将从联合模型得到的最大似然函数与从两个简化模型得到的最大似然函数进行对比,实现对h0:α=0或h0:γ=0的似然比检验。
将此模型和算法一起称为具有egger假设的多结局概率孟德尔随机化(mopmr-egger)方法。其中,“mo”指的是对多个结局(multipleoutcome)的建模。“概率”是指mopmr-egger模型完全模仿了twas背后的数据生成原理和似然推断程序。“egger”代表水平多效性的假设,参数γ将egger回归假设有效推广到到具备ld相关结构的工具变量和多个结局。
当所述分析方法对汇总统计量数据进行分析时,模型可表示如下:
其中,
本发明的第二个方面,提供一种基于孟德尔随机化的多性状全转录组关联分析系统,所述系统包括:
数据获取单元,用于获取相关数据信息并进行标准化处理;
模型构建单元,用于基于获取的数据进行多结局建模,在似然框架下同时估计和检验基因对多个结局性状的因果效应,同时能将潜在的水平多效性嵌入模型。
其中,当所述系统对个体水平数据进行分析时,
所述数据获取单元获取的相关数据信息包括但不限于基因表达的个体数据、表达数据对应的基因信息,全基因组关联分析的多维性状数据和全基因组关联分析对应的基因信息。
进一步的,上述相关数据信息均需要标准化处理。
所述模型构建单元中采用如下回归模型:
尽管上述三个公式针对的是两个独立的研究,但参数β将二者紧密的结合起来。式(2)-(3)可以合并为
其中,
遵循遗传学中常用的多基因建模假设,假设β的所有元素非零,且每个元素都服从正态分布
当所述系统对汇总统计量数据进行分析时,
所述数据获取单元获取的相关数据信息包括但不限于基因表达的汇总数据,全基因组关联分析的多维性状汇总数据,基因表达遗传变异的连锁不平衡矩阵,全基因组关联分析遗传变异的连锁不平衡矩阵和纳入分析的性状间的相关矩阵。
所述模型构建单元中采用如下模型:
其中,
本发明的第三个方面,提供一种电子设备,包括存储器和处理器以及存储在存储器上并在处理器上运行的计算机指令,所述计算机指令被处理器运行时,完成上述基于孟德尔随机化的多性状全转录组关联分析方法所进行的步骤。
本发明的第四个方面,提供一种计算机可读存储介质,用于存储计算机指令,所述计算机指令被处理器执行时,完成上述基于孟德尔随机化的多性状全转录组关联分析方法所进行的步骤。
本发明的第五个方面,提供上述方法、系统、电子设备和/或计算机可读存储介质在如下任意一种或多种中的应用:
1)复杂疾病内在分子遗传机制研究;
2)疾病易感性研究;
3)药物反应研究;
4)药物靶标研究;
5)药物筛选研究。
上述一个或多个技术方案的有益技术效果:
上述技术方案提供一个多性状twas联合分析方法,称之为mopmr-egger。mopmr-egger一次检验一个基因,将存在特定基因包含的连锁不平衡顺式snps作为工具变量,实现对多个性状因果效应的联合检验。同时,mopmr-egger能够检验和控制工具变量潜在的水平多效性,从而能够最大限度提高检验效能且避免了twas中的错误关联。大量统计模拟证实mopmr-egger对因果效应的检验具有稳定的一类错误,且比现有twas分析方法具有更高的检验效能。进一步,使用mopmr-egger分析了英国生物样本库中五个类别的11个性状,结果显示,mopmr-egger比单变量twas方法多发现了约13.15%的基因关联,并清晰揭示了收缩压和舒张压的不同生物调节机制。因此具有良好的实际应用之价值。
附图说明
构成本发明的一部分的说明书附图用来提供对本发明的进一步理解,本发明的示意性实施例及其说明用于解释本发明,并不构成对本发明的不当限定。
图1为本发明mopmr-egger模型示意图以及在不同情形下mopmr-egger与单性状方法的检验效能对比。(a)mopmr-egger可以应用于twas研究,在混杂因素(u,未展示)存在的情况下,以cis-snps(z)作为工具变量,来估计基因的表达(x)对多个性状(y1,…,yk)的因果效应。mopmr-egger依赖于一个联合似然框架,可以矫正水平多效性(y1,…,yk)和多性状之间的相关性。(b-g)基于mopmr-egger的多性状联合模型在不同场景下都优于单性状方法,比如每次只能分析一种性状的pmr-egger方法。对两个性状(y1,y2)的简单示例性模拟可以概括为以下六种情形。(b)基因影响两个相关性状,其对这两个性状的因果效应与这两个性状的关联方向相反。(c)基因影响两个不相关的性状。(d)基因影响两个相关性状,其对这两个性状的因果效应与这两个性状的关联方向相同。(e)基因只影响两个相关性状中的一个。(f)基因只影响两个不相关性状中的一个。(g)基因不影响任何性状。b-f中y轴表示检验效能,g中y轴表示i类错误。
图2为本发明不同模拟情形下因果效应检验的i类错误和检验效能。(a,b)在零假设成立时,水平多效性存在或不存在时因果效应检验的-log10p值的分位数图。根据不同水平多效性效应大小构建不同零假设的模拟:(a)γ=(0,0,0,0)t(b)γj从(0,1×10-4,5×10-4,1×10-3,2×10-3)中随机选取,j=1,2,3,4.在一定的水平多效性范围内,mopmr-egger具有较好的因果效应检验的i类错误。(c-f)在异质性因果效应设定下,基于bonferroni多重校正阈值因果效应的检验效能为y轴,第一个性状的pvezy为x轴,其它四个性状的pvezy是第一个性状pvezy的15%,50%和85%。比较方法包括mopmr-egger、pmr-egger、predixcan和twas。不同的线条符号代表四种性状是否相关(c)、因果效应的方向(d,e,f)。在不存在水平多效性效应的情况下,对受影响的性状数量从1到4进行模拟(c-f).
图3为本发明不同模拟情形下水平多效性检验的i类错误和检验效能。(a,b)在零假设下,因果效应存在或者不存在时检验水平多效性的-log10p值的分位数图。根据不同因果效应值构建不同零假设的模拟:(a)pvezy=(0,0,0,0)t;(b)pvezy,j从(0,0.005,0.01,0.015,0.02)中随机选取,j=1,2,3,4.(a)γ=(0,0,0,0)t(b)γj从(0,1×10-4,5×10-4,1×10-3,2×10-3)中随机选取,j=1,2,3,4.在一定的因果效应范围内,mopmr-egger具有较好的水平多效性检验的i类错误。(c-f)在不同的模拟情形下,检验水平多效性效应的mopmr-egger和pmr-egger的检验效能。基于bonferroni多重校正阈值的水平多效性检验效能为y轴,pvezy为x轴。模拟在相关性状(d,f),独立性状(c,e),水平多效性为γ=(0,1×10-4,5×10-4,1×10-3)t(c,d),水平多效性为(1×10-4,5×10-4,1×10-3,2×10-3)t(e,f)下进行。
图4为本发明mopmr-egger和pmr-egger方法对ukbiobank中五个性状类别的twas分析结果。检验不同性状因果效应值的-log10p值分位数图:(a)血压性状类;(b)身体测量指标类;(c)血细胞计数类;(d)白细胞指标类;(e)红细胞指标类。检验不同性状水平多效性效应的-log10p值分位数图:(f)血压性状类;(g)身体测量指标类;(h)血细胞计数类;(i)白细胞指标类;(j)红细胞指标类。比较方法有mopmr-egger、单性状pmr-egger(不同性状表示为不同颜色)。sbp,收缩压;dbp,舒张压;bmi,身体质量指数;fvc,最大肺活量;rbc,红细胞计数。
图5为本发明mopmr-egger和pmr-egger对血压性状类的基因进行go功能和kegg通路富集分析。点图展示了对sbp和dbp识别出具有相同因果效应方向的基因(a)和具有相反因果效应方向的基因(c)前十个富集gobp、cc和mf条目的结果。点图展示了对sbp和dbp识别出具有相同因果效应方向的基因(b)和具有相反因果效应方向的基因(d)前十个富集kegg通路的结果。点的颜色表示基于q值富集分析的统计显著性,点的大小表示每项包含基因的比例。sbp,收缩压;dbp,舒张压;go,基因本体;bp,生化过程;cc,细胞成分;mf,分子功能;kegg,京都基因和基因组百科全书。
具体实施方式
应该指出,以下详细说明都是例示性的,旨在对本发明提供进一步的说明。除非另有指明,本文使用的所有技术和科学术语具有与本发明所属技术领域的普通技术人员通常理解的相同含义。
需要注意的是,这里所使用的术语仅是为了描述具体实施方式,而非意图限制根据本发明的示例性实施方式。如在这里所使用的,除非上下文另外明确指出,否则单数形式也意图包括复数形式,此外,还应当理解的是,当在本说明书中使用术语“包含”和/或“包括”时,其指明存在特征、步骤、操作、器件、组件和/或它们的组合。应理解,本发明的保护范围不局限于下述特定的具体实施方案;还应当理解,本发明实施例中使用的术语是为了描述特定的具体实施方案,而不是为了限制本发明的保护范围。下列具体实施方式中如果未注明具体条件的实验方法,通常按照本领域技术内的分子生物学的常规方法和条件,这种技术和条件在文献中有完整解释。
以下通过实施例对本发明做进一步解释说明,但不构成对本发明的限制。应理解这些实施例仅用于说明本发明而不用于限制本发明的范围。
实施例
材料和方法
mopmr-egger概述
mopmr-egger依托两样本mr框架,该框架在没有样本重叠的两项独立研究中测量暴露和结局,旨在估计和检验暴露对结局的因果效应。在twas框架下,暴露是在基因表达研究中测量的基因表达水平,而结局是在gwas中测量的多个相关性状。mopmr-egger一次检验一个基因,并将cis-snps作为工具变量,能够在似然框架下同时估计和检验基因对多个结局性状的因果效应,同时能够将潜在的水平多效性嵌入模型。图1a给出了mopmr-egger模型的示意图。
具体模型的数学表达式可以表述如下,记x为n1维向量,表示n1个个体在基因表达研究中的基因表达水平,zx为n1×p维的cis-snps基因型矩阵,表示在基因表达研究中对应于该基因的p个工具变量,y为一个k×n2维的矩阵,表示gwas研究中n2个个体的k个相关性状的测量值,zy为对应于p个相同工具变量的gwas研究中n2×p维的基因型矩阵。不失一般性,假设x和yt,zx,zy的每一列都实行了标准化。考虑如下三个回归模型:
式(1)刻画了基因表达研究中特定基因的cis-snps与其表达水平的关系,式(2)-(3)描述了gwas研究中预测的基因表达和多维相关性状之间的关系。μx是一个标量,
其中
需要特别说明的是,组学数据研究中p往往远大于n1,因此需要对β做一定的建模假设以保证模型可识别性。类似的,也需要对γ做额外的建模假设,否则,式(4)中定义的两个工具变量效应项:垂直多效性α(zyβ)t和水平多效性
在上述联合模型中,所关心的参数是基因在多个结局性状上的因果效应α。α的因果效应识别和可解释性可以基于因果推断中的决策理论加以证明。和传统的mr分析一样,α的因果解释至少需要两个假设成立:(1)工具变量与基因表达有关;(2)工具变量与基因表达和每个结局都有关的任何其他混杂因素无关。因为对水平多效性γ做了明确的模型假设,mopmr-egger不再要求满足mr的一般排除限制条件(即,工具变量只能通过基因表达途径影响每个结局)。然而,对γ的模型假设需要满足工具变量强度与直接效应独立的假设(instrumentstrengthindependentofdirecteffect,inside),这个假设要求工具变量-基因表达效应和工具变量-结局效应是相互独立的,有时称为弱排除限制条件。因为混杂因素往往是未知的,这些假设有许多在实践中是无法检验的,本研究所使用的术语“因果效应”,只是为了强调α的估计比y对
在上述模型中,感兴趣的是在水平多效性γ存在时,估计因果效应α并检验原假设h0:α=0,拒绝原假设α=0意味着基因表达至少对一个性状有非零的因果效应。另外,还可对水平多效性γ进行估计和检验h0:γ=0,拒绝原假设γ=0说明cis-snps至少对一个性状有非零的水平多效性。在统计推断层面,发展了期望最大化(em)算法的参数扩展版本(px-em),通过最大化基于式(1)和(4)定义的联合似然来进行参数推断。可以获得最大似然联合模型以及α和γ最大似然估计。此外,进一步将该em算法应用于两个简化模型,一个模型中不包含α,另一个模型中不包含γ,分别获得对应的最大似然。最后,将从联合模型得到的最大似然函数与从两个简化模型得到的最大似然函数进行对比,实现对h0:α=0或h0:γ=0的似然比检验。
将此模型和算法一起称为具有egger假设的多结局概率孟德尔随机化(mopmr-egger)方法。其中,“mo”指的是对多个结局(multipleoutcome)的建模。“概率”是指mopmr-egger模型完全模仿了twas背后的数据生成原理和和似然推断程序。“egger”代表水平多效性的假设,参数γ将egger回归假设有效推广到到具备ld相关结构的工具变量和多个结局。
基于汇总数据(summarystatistics)的mopmr-egger模型
考虑到对汇总数据的分析已经成为科学热点,进一步发展了基于汇总数据的mopmr-egger模型。记∑1为基因表达研究中特定基因cis-snps间的snp-snp相关矩阵(即,ld矩阵)。∑2为gwas数据中对应的相关矩阵。这两个矩阵都是p×p维的半正定矩阵。通常,∑1,∑2都可以用ld参考面板数据中相应种族的个体数据进行估算(例如,千人基因组计划)。基于汇总数据的mopmr-egger模型可表示如下
其中,
模拟
进行了跨基因模拟设计来评估mopmr-egger的性能,并将其与现有twas方法进行比较。先从geuvadis数据中随机选择10,000个基因,并提取这些基因对应的cis-snps,基因cis-snps的中位数为576个(最小值为11;最大值为7409)。对每个特定基因,分别利用基因表达研究和gwas研究获得的基因型数据,依次模拟其表达水平和结局性状。具体来讲,首先从geuvadis数据中获得了每个基因的p个cis-snps的基因型,得到了标准化的基因型矩阵zx之后,从正态分布n(0,pvezx/p)中模拟snps对基因表达的效应β,其中,pvezx表示基因表达变异被遗传效应解释的比例。对所有cis-snps的遗传效应求和为zxβ。进一步,从正态分布n(0,1-pvezx)中模拟了残差εx,最后将遗传效应和残差相加,得到基因表达水平。
接下来,在kaiserpermanente/ucsf成人健康和老龄化遗传流行病学(kaiserpermanente/ucsfgeneticepidemiologyresearchstudyonadulthealthandaging,gera)数据中随机从对照人群中选择2000个个体相同的p个cis-snps,获得标准化的基因型矩阵zy,针对四个相关结局性状使用基因表达数据中相同的snp效应大小β,设置四个因果效应
最基本的模拟情形设置为:n1=465,n2=2000,pvezx=10%,pvezy=(0,0,0,0)t,γkj=0(j=1,…,p;k=1,…,4).在该基本设置的基础上,每次改变一个参数,以探索各种参数对模型的影响。对于pvezx,设置为1%,5%或10%,这三个值都接近基因表达遗传度估计的中位数。对于β,考察了偏离多基因假设的不同分布,随机选择1个snp,1%或10%的snps对基因表达有非零效应,并且从正态分布中模拟非零效应来解释一个固定pvezx.对于水平多效性效应γ,为避免人为设定每个γj(j=1,2,3,4)的取值对结果的影响,随机从0,1×10-4,5×10-4,1×10-3,2×10-3选择一个取值,,这些取值是依托真实数据估计出来的水平多效性效应的0%、50%、70%、90%、95%分位数。同时,从0%、10%、30%、50%,100%中随机选择四个比例值,作为四个性状上具有非零水平多效性的snps的比例。进一步,还研究了定向多效性设置(水平多效性效应负与正的snps比值为0∶10)、近似定向多效性设置(1∶9或3∶7)和平衡多效性设置(5∶5).对于ω,除了使用从真实nfbc数据估计的ω之外,还研究了ω为单位矩阵及其ω的每个元素有指数协方差结构ωi,j=ρ|i-j|的情形,ρ取0.5,0.7,0.9.此外,研究了β之间相关的情形,模拟snps对基因表达的效应服从协方差矩阵为w∑的多元正态分布,∑是snps的ld矩阵,w是一个标量,以确保pvezx=10%.对于pvezy,除了上述零因果效应的基本设置外,还考察了同质因果效应设置和异质因果效应设置两种情形。在同质因果效应设置中,pvezy的所有元素都具有相同的值v,v为0.5%/4,1%/4,1.5%/4,2%/4.在异质的因果效应的设置中,第一个性状因果效应为v,其他三个性状的因果效应为0.15v,0.85v和0.50v,v分别是0.5%,1%,1.5%或2%.在效应的方向上,分别在同质和异质因果效应设置中随机选取了基因表达所影响的四个相关性状中的一、二、三、四个性状。当基因表达影响两个性状时,对其中一个性状的影响与对另一个性状的影响效应符号是相反的。当基因表达影响三个性状时,其对随机选择的两个性状的影响与对第三个性状的影响是效应符号相反的。当基因表达影响四个性状时,其对随机选择的两种或三种性状的影响与对另外两种或一种性状的影响效应符号是相反的。
对于i型错误检验,对上述每个设置情形执行了10,000次模拟。对于检验效能计算,使用了两种不同的计算方法。在第一种方法中,进行了1,000次备择假设成立时的模拟,并基于bonferroni多重校正的p值阈值比较了检验效能(多变量方法为0.05/1000,单变量方法为0.05/4000)。在第二种方法中,为每个模拟情形执行了100个备择假设成立的模拟和900个原假设成立的模拟,并在错误发现率(falsediscoveryrate,fdr)为0.05的标准下计算检验效能。同时,基于一种上述模拟情形,也对基于汇总数据的mopmr-egger模型进行了评估(详情见讨论)。
为了更好地说明mopmr-egger模型,考虑了水平多效性存在时两个性状的不同基因因果关联模式,设置n1=465,n2=2000pvezx=10%,γ=(0.0001,0.0005)t,基因表达影响两种性状:pvezy=(0.01,0.01)t,基因表达只影响一种性状:pvezy=(0.01,0)t,基因表达对这两种性状都没有影响:pvezy=(0,0)t,性状间的相关性ρ=0.66,性状独立时ρ=0.需要指出的是,ρ=0.66对应于英国生物样本库(ukbiobank)中估算的收缩压(systemicbloodpressure,sbp)与舒张压(diastolicbloodpressure,dbp)的相关系数。总体而言,研究了水平多效性存在时,考虑三种因果效应值设置和两个性状相关性设置的六种基因因果关联模式。考虑到单性状twas方法中,只有pmr-egger可以解释水平多效性,因此,对于每一种情况,比较了mopmr-egger与pmr-egger的性能。对于i类错误,进行了100次1,000个零假设下的模拟,计算了mopmr-egger在100次重复中p值小于0.05/1000的频率,pmr-egger100次重复中p值小于0.05/2/1000的频率。对于检验效能,进行了1,000次备择假设成立时的模拟,并基于bonferroni多重校正的p值阈值比较了检验效能。
与mopmr-egger相比较的方法
目前还没有多性状twas分析方法,因此,比较了三种常用的单性状twas方法,包括:(1)pmr-egger,使用多个相关的snp工具变量对水平多效性进行检验和控制。pmr-egger模型使用了所有cis-snps作为工具变量,并使用r包pmr中的pmr_individual函数来检验因果效应和水平多效性效应。(2)predixcan,使用多个相关的snp工具变量,但不控制水平多效性。predixcan使用了所有cis-snps,并使用r包glmnet执行elasticnet来获得cis-snps对基因表达的系数估计。(3)twas,采用多个相关的snp工具变量,但不控制水平多效性。twas使用了所有cis-snps,并使用gemma软件中bslmm方法来获得cis-snps对基因表达的系数估计。总体而言,这些方法都属于两样本设计,都能计算p值来检验因果效应αi,i=1,…,4.然而,这三种方法的先验假设有所不同:predixcan依赖于弹性网假设;twas依赖于贝叶斯稀疏线性混合模型假设;而pmr-egger依赖于正态先验假设。在推断上,predixcan和twas依赖于两阶段回归,而pmr-egger则是基于最大似然。在比较过程中,采用单性状twas方法一次分析一个性状,从而根据bonferroni多重校正的p值阈值判定基因关联显著性,该阈值调整了检验的基因数量和性状数量。
此外,考虑到bonferroni矫正或许会降低单性状twas方法的检验效能,进一步提出了单性状twas分析的最小p值策略,对于每种单性状方法和一个特定基因,获得多个性状的最小p值,将其作为该基因的因果关联证据。因为获得最小p值的统计量分布并不容易,所以设定fdr水平为0.05,比较了mopmr-egger和单性状最小p值法的检验效能。对于实际数据分析,首先对个体进行10次随机置换,同时保持性状之间的相关性。然后,将每种方法应用于置换后的数据,以获得最小p值的统计量分布,据此计算fdr,并基于fdr阈值0.05计算因果关联基因的个数。
实际数据应用
通过整合geuvadis基因表达数据和ukbiobank的gwass,应用mopmr-egger进行多性状twas分析。获得了geuvadis数据作为基因表达数据,并从ukbiobank中提取11个性状,这些性状在先前研究中均有报道,其遗传度均大于0.2。将这些结局性状分为以下五类:血压(sbp和dbp)、身体测量指标(身高、体重指数、肺活量(fvc)和fev1-fvc比率)、血细胞计数(血小板计数、红细胞计数、嗜酸性粒细胞数和白细胞计数)、白细胞指标(嗜酸性粒细胞计数和白细胞计数)和红细胞指标(红细胞计数和红细胞分布宽度(rdw))。可以发现,白细胞指标类是血细胞计数类的一个子集。对于每一个类别,使用mopmr-egger和其所比较的方法来分析这五个类别中的性状。下面详细介绍geuvadis和ukbiobank的数据处理流程和步骤。
geuvadis数据包含了465个个体的基因表达测量值,这些个体来自5个不同的群体,包括ceph(ceu)、芬兰人(fin)、英国人(gbr)、托斯卡尼人(tsi)和约鲁巴人(yri)。在表达数据中,只关注在gencode(release12)中注释的蛋白编码基因和lincrnas.在这些基因中,剔除了至少在一半的个体中没有计数的低表达基因,最终得到15,810个基因。根据之前的研究,进行了peer归一化以消除混杂效应和多余的变异。随后,为了消除剩余的群体分层,对每个群体中个体的基因表达测量值进行分位数标准化,以达到标准正态分布,然后对来自所有五个群体的个体的基因表达测量值进行分位数标准化,以达到标准正态分布。除了表达数据外,geuvadis的所有个体也在千人基因组计划中进行了基因型测序。千人基因组项目3期中获得基因型数据。过滤掉了具有哈迪-温伯格平衡(hwe)p值<10-4,基因型召唤率<95%,或次要等位基因频率(maf)<0.01的snps,总共保留了7,072,917个snps进行分析。
ukbiobank数据包括487,298个个体和92,693,895个填补的snps。遵循neale实验室(https://github.com/nealelab/uk_biobank_gwas/tree/master/impuing-v2-gwas)相同的样本质量控制程序,保留了总计337,129个欧洲血统的个体。过滤了hwep值<10-7、基因型召唤率<95%或maf<0.001的snps,总共得到13,876,958个snps。对每个性状依次进行性别和前10个主成分(pcs)的标准化表型回归得到残差,将残差标准化,使其均值为0,标准差为1,最后利用这些标准化的残差进行twas分析。
将geuvadis数据与ukbiobank中的gwass数据进行整合,进行twas分析。对于geuvadis数据中的每个特定基因,依次提取了位于转录起始位点(tss)上游100kb或转录末端位点(tes)下游100kb区间内的cis-snps。将geuvadis中的这些snps与ukbiobank中获得的snps取交集,得到共同的snps集。geuvadis和ukbiobank重叠的所有基因的cis-snps的平均个数为497(中位数为443,最小值为1,最大值为8085)。然后,对于每一对基因(来自geuvadis)和性状类别(来自gwas),依次运行多性状mopmr-egger方法和单性状pmr-egger方法来检验基因表达和每个类别中多个性状之间的因果关系。为了比较mopmr-egger和pmr-egger,依据bonferroni多重校正阈值作为显著性的标准:mopmr-egger为0.05/15,810,pmr-egger为0.05/(15,810*k),k为每个类别中结局性状的数量。
在五个类别中,重点深入分析了血压这一类别。血压类包含sbp和dbp两个性状,两者之间的相关性估计为0.66。血压是一个复杂的性状,遗传度约在30-50%范围内。许多大规模的gwass研究了血压的遗传机制。重要的是,血压升高是导致中风和冠状动脉疾病风险的强有力且可改变的风险因素,而中风和冠状动脉疾病是全球死亡和疾病的主要原因。对于血压类别,除了mopmr-egger和pmr-egger,还应用了pmr-egger、twas和predixcan的最小p值方法。对于这些最小p值方法和每个特定基因,依次分析类别中的每个性状,并获得这些性状间的最小p值,作为该特定基因因果关联的证据。对个体进行了10次随机置换,借此获得最小p值的统计量分布,并据此计算出fdr。在mopmr-egger分析中,依据基因对两种性状的效应大小和方向,将具有统计显著性的基因分为两组:在两种性状上具有相同效应符号的基因和在两种性状上具有相反效应符号的基因,针对这两组不同的基因进一步通过r包clusterprofiler使用基因本体(go)和京都基因和基因组百科全书(kegg)进行富集分析,并根据q值阈值0.05来声明基因集的显著性。
结果
mopmr-egger模型概览
简单来讲,mopmr-egger一次检验一个基因,并估计和检验某特定基因对多个结局性状的因果效应。与现有的twas方法不同,mopmr-egger采用了具有ld相关关系的多个snp工具变量,在最大似然框架下实现twas的统计推断,能够检验和控制twas中广泛存在的水平多效性效应,同时联合分析多个相关性状,借此提高了twas分析的能力。首先总结了图1b-g中两个示范性状的mopmr-egger和pmr-egger的比较结果。当基因影响两个性状,mopmr-egger在基因效应与性状相关性方向相反时较高的检验效能(图1b),紧随其后的是两个性状是独立的情形(图1c)、基因效应与性状相关性方向相同的情形(图1d)。而pmr-egger的检验效能在这三种情况下几乎相同(图1b-d)。出现这种结果的潜在可能的原因是,当二者方向相同时,mopmr-egger很难区分因果效应和性状间相关性。当基因只影响一种性状时,通过利用两种性状之间的相关性,mopmr-egger的检验效能仍然高于pmr-egger(图1e),而当两种性状相互独立时,mopmr-egger与pmr-egger的检验效能几乎相同(图1f)。总的来说,相对于pmr-egger,mopmr-egger的检验效能在大多数情况下要高得多。此外,当基因对这两种性状都没有因果效应时,mopmr-egger得到了校准的i型误差控制,而pmr-egger在0.05的期望值下略微膨胀(图1g)。
模拟:检验和估计因果效应
通过全面的模拟来检验mopmr-egger的有效性,并将其与twas的现有方法进行了比较。材料和方法中提供了具体的模拟。简单地说,依靠真实的基因型数据,模拟基因表达以及四个结局性状,使用mopmr-egger来分析这四个性状,一次一个基因。在总共287个模拟情形下(因果效果检验的25个零假设情形和152个备择假设成立的情形;水平多效性效果检验的22个零假设情形和88个备择假设情形)考虑了mopmr-egger因果效应检验和水平多效性检验的一类错误控制和检验效能。
第一组模拟针对因果效应检验,首先在零假设下检验了mopmr-egger的i型错误控制。结果发现,无论是在存在水平多效性效应(图2a)还是不存在水平多效性效应(图2b)情况下,mopmr-egger都较好的控制了i型错误,而且无论基因表达的遗传结构是稀疏的还是多基因的,无论基因表达遗传度,无论snp对基因表达的影响是否与ld相关,无论多个性状是否相关,mopmr-egger始终能够较好的控制i型错误。需要注意的是,当基因表达遗传度较低时,mopmr-egger的p值略微保守,这可能是由于联合似然提供的信息有限,渐近正态分布不能很好地近似。
mopmr-egger对水平多效性做了一个相对强的egger假设,该假设要求对于给定的性状,所有snp都具有相同的水平多效性效应。为了检验这种假设的稳健性,随机选择固定比例的snp,而不是全部snp,具有水平多效性效应。结果发现,无论水平多效性snp的稀疏性如何,mopmr-egger都能很好的控制i类错误。除了正向和负向效应snp的比例设置为0:10外,还通过随机分配相应比例的snp,检验了两种近似方向多效性设置(1:9或3:7)和一种平衡设置(5:5)。结果表明,当每个性状的水平多效性效应较小或中等时,mopmr-egger在近似方向性多效性设置或平衡设置中较好的控制i类错误。然而,当某一性状的水平多效性效应很大时,正如预期的那样,mopmr-egger出现了i类错误膨胀问题。总体而言,mopmr-egger在检验因果效应零假设下表现良好。
接下来,评估了mopmr-egger识别非零因果效应的检验效能,并将其与三种单变量方法进行比较。在大多数模拟情形下,mopmr-egger比单变量twas方法更强大。在总共152个模拟情形中,与pmr-egger、predixcan和twas相比,mopmr-egger获得了平均53.12%、42.40%和36.79%的检验效能增益。不管因果效应在不同的性状间是同质的还是异质的(图2c-f),无论基因影响一个性状或多个性状,不管性状是如何相互关联,存在或不存在水平多效性,mopmr-egger始终具有大量的检验效能增益。唯一的例外是当四个性状是相互独立情形,且基因只与四个性状中的一个相关(图2c)。在这种情况下,mopmr-egger的低检验效能可能是因为mopmr-egger使用了额外的参数来对多个相关性状的非零随机效应进行建模,从而导致自由度的损失,进而降低了检验效能。然而,即使基因只与四个性状中的一个相关,当性状之间相互关联时,mopmr-egger仍然比其他方法具有更大的检验效能(图2c)。值得注意的是,mopmr-egger和pmr-egger可以控制水平多效性,而predixcan和twas则不能控制水平多效性。因此,在水平多效性存在的情况下,predixcan和twas无法控制i类错误,p值被夸大。如果将所有的p值进行校准,并依赖于一个名义p值阈值,而不是正确的i类错误阈值,那么predixcan和twas似乎比pmr-egger具有更高的检验效能。尽管如此,基于名义p值阈值的predixcan和twas的检验效能始终低于mopmr-egger,这进一步突出了多性状联合建模的重要性。
不同方法的检验效能和mopmr-egger带来的检验效能增益取决于几个重要参数。首先,无论水平多效性是否存在,所有方法的检验效能都随着因果效应的减少而降低。然而,在所有方法中,mopmr-egger的检验效能降低趋势是最不明显的,表明mopmr-egger具有一定程度的稳健性能。第二,mopmr-egger采用了多性状联合建模,并将性状间的相关关系考虑在内。因此,当性状之间的相关性增加时,mopmr-egger的检验效能增加,而其他方法的检验效能基本保持不变。第三,对多性状联合建模所带来的检验效能增益取决于基因表达对性状的因果效应是否与性状相关性方向相同。当两种性状之间存在正相关关系,对两个性状的因果效应相反时的检验效能要高于对两个性状因果效应相同时候的检验效能;反之亦然(图2d)。最后,由于mopmr-egger考虑了snps对多个性状的水平多效性效应。因此,无论受水平多效性影响的性状数量或水平多效性效应的大小如何变化,mopmr-egger仍然有效,而其他方法则无效。
在上述模拟中,主要比较了mopmr-egger与现有三种单性状的twas方法。进一步,还比较了mopmr-egger和这些单性状twas方法最小p值策略。首先获得给定基因关联证据的不同性状间的最小p值,并在fdr0.05的水准下,计算了不同方法的检验效能。与先前的模拟结果一致,无论因果效应对于不同性状是同质的还是异质的,无论水平多效性是否存在,mopmr-egger仍然比pmr-egger,predixcan,twas的检验效能高。不同于上述bonferroni调整阈值的结果,在fdr标准下,当存在水平多效性效应时,predixcan和twas均显示较低的检验效能。
最后,无论水平多效性是否存在,mopmr-egger在零假设和各种备择假设下,均给出了因果效应的准确估计。
模拟:检验和估计水平多效性效应
第二组模拟主要是针对水平多效性效应的检验。与一般的twas/mr方法相比,mopmr-egger能够检验snps是否对任一结局性状表现出非零的水平多效性效应。
首先在零假设下检验了mopmr-egger对水平多效性效应的一类错误控制情况,在零假设条件下,即,任何一个遗传变异对4个性状都不存在水平多效性效应。发现无论因果效应是否存在(图3a,b),无论多个性状之间的相关性大小,因果效应不存在时无论基因表达的基因结构是稀疏或多基因,mopmr-egger对水平多效性的检验均能很好的控制i类错误。然而,当模型假设以多种方式不成立时,例如,当基因表达的基因结构是稀疏的,当基因影响两种以上性状时,mopmr-egger就会出现i类错误膨胀问题。总体来说,在零假设下,mopmr-egger对水平多效性的检验均能较好的控制i类错误。
接下来,评估了mopmr-egger识别非零水平多效性效应的效能。由于pmr-egger是目前唯一可以为水平多效性效应提供检验的方法,为此,重点比较了mopmr-egger和pmr-egger的检验效能。模拟发现,pmr-egger和mopmr-egger的检验效能随着水平多效性的增加而增加,在一系列设置中,mopmr-egger的表现优于pmr-egger(图3cvs图3e,图3dvs图3f)。与上述因果效应的模拟一致,当四个性状彼此不相关时,mopmr-egger与pmr-egger具有类似的检验效能(图3c,e),然而,当性状间存在相关性时,mopmr-egger优于pmr-egger(图3d,f)。此外,无论是否存在因果效应,在一系列稀疏水平范围内,mopmr-egger仍然比pmr-egger更有效,这两种方法的检验效能均随着水平多效性稀疏程度的增加而减小。同样,与因果效应检验的结果一致,两种方法在多效性检验中,在没有定向水平多效性的情况下,效果都很差。进一步将mopmr-egger与pmr-egger的最小p值方法进行了比较,得到了一致的结果。
最后,在存在定向水平多效性时,mopmr-egger可以准确地估计水平多效性效应。然而,在没有定向多效性效应的情况下,多效性效应估计值是有偏的。
实际数据应用
将geuvadis的基因表达数据与来自ukbiobank五个类别的11个性状的gwas数据进行整合(详见材料和方法部分),应用mopmr-egger进行了twas分析。geuvadis研究的基因表达数据共包括15,810个基因,ukbiobank的五个性状类别包括:血压类别、身体测量指标类别、血细胞计数类别、白细胞指标类别和红细胞指标类别。
展示了每个类别中检验每个基因对mopmr-egger性状的因果效应的p值,以及每个类别中单性状pmr-egger方法的p值(图4a-e)。predixcan和twas两种方法本质上不能控制水平多效性,且这两种方法往往出现p值膨胀问题,因此,本研究并未采用predixcan和twas方法分析,相反,将在下一段中采用这两种方法的最小p值策略进行深入分析。结果显示mopmr-egger和pmr-egger的p值都表现良好,在全转录组bonferroni多重校正阈值下,mopmr-egger识别出的基因数目比pmr-egger多13.15%的基因(表1),这突出了在twas中多性状联合分析的优势。pmr-egger识别的基因(89.29%)大部分亦能被mopmr-egger检测到,且mopmr-egger方法的因果关联显著性增加。例如,tfrc基因被识别出与rdw相关(pmr-eggerp=3.22×10-17),但当所有红细胞指标类别的性状联合在一起时,关联证据明显变强(mopmr-eggerp=5.72×10-22)。tfrc编码经典转铁蛋白受体,参与细胞的铁吸收。tfrc中多个snps已被证实与gwas研究中多种红细胞表型相关。这些相关的红细胞表型包括红细胞平均血红蛋白(meancorpuscularhemoglobin,mch)和红细胞平均体积(meancorpuscularvolume,mcv),均与rdw密切相关。tfrc的变异可能正如在tfrc缺乏的小鼠中观察到的那样,导致红细胞前体铁可用性降低,从而导致rdw测量的红细胞大小代偿性增加。更重要的是,mopmr-egger识别了许多未能被pmr-egger识别的基因。例如,在血压类中,只有mopmr-egger发现了ephb4基因(mopmr-eggerp=1.41×10-8,sbppmr-eggerp=0.98,dbpp=5.33×10-4)。ephb4编码ephrinb型受体4,该受体与ephrin-b2结合,在血管发育和血管生成中发挥重要作用。先前的研究表明,在小鼠中,ephb4的缺失会导致低血压,这支持了ephb4调节血压的因果作用。
随后,对血压类进行了深入的分析,它只包含两种性状(sbp和dbp)。除了与上述pmr-egger方法进行比较外,还将mopmr-egger与pmr-egger、predixcan、twas的最小p值方法进行了比较。计算了不同方法在fdr为0.05的标准下的结果。结果发现,mopmr-egger比其他方法识别了更多的基因,再次验证了多性状联合建模的优势。mopmr-egger、pmr-egger、predixcan和twas识别出的显著基因数量分别为765、691、90和83,这也说明基于似然的mopmr-egger和pmr-egger方法比基于两阶段回归推断的predixcan和twas方法具有更高的效能。在mopmr-egger鉴别出的显著基因中,约有40%(301/765)对这两个性状具有相反的因果效应方向。go和kegg通路富集分析(图5)显示,对两种性状具有相同因果效应方向的基因在抗原加工呈递(q=1.96×10-4;图5a)、人类t细胞白血病病毒1感染(q=0.03)、病毒性心肌炎(q=0.03)和iga产生的肠道免疫网络(q=0.04;图5b)通路显著富集。这种在炎症和诱导免疫反应途径中的富集支持了最近揭示的它们在调节血压中的作用。事实上,炎症激活先天和适应性免疫反应,导致血管系统、肾脏和交感神经系统(sns)的改变,最终导致血压长期升高。相反,对两种性状具有相反因果效应方向的基因在cop9信号体(q=0.02;图5c)和溶酶体(q=5.14×10-4;图5d)通路中显著富集。cop9信号体和溶酶体途径的富集支持了它们在维持血管稳态和可塑性以及随后的血压调节中的关键功能。cop9信号体和溶酶体都控制着血管系统中的泛素化和随后的蛋白循环调节。血管中的蛋白质泛素化和循环决定了血管张力和硬度,这可能在细胞收缩和舒张的心脏周期中对sbp和dbp产生不同的影响。
接下来,关注水平多效性效应的检验。展示了5个类别两种方法(mopmr-egger和pmr-egger)基因水平多效性检验的p值(图4f-j)。mopmr-egger和pmr-egger的p值均表现良好,mopmr-egger识别出的水平多效性基因总数比pmr-egger多17.10%(表1)。具体来说,mopmr-egger在血压类中识别出56个基因,在身体测量类中识别出275个基因,在血细胞计数类中识别出383个基因,在白细胞指标类中识别出146个基因,在红细胞指标类中识别出153个基因。相比之下,pmr-egger识别出的基因数分别是26、196、266、106和136。pmr-egger发现的大部分基因(71.53%)也被mopmr-egger所包含。在mopmr-egger识别的水平多效性基因中,36.16%具有显著的因果效应,同时,具有显著的因果效应基因中,11.64%具有水平多效性效应。具有水平多效性效应的基因与具有因果效应的基因之间明显的重叠,突出了在twas建模分析时同时考虑这两种效应的重要性。血压类别的深入分析也显示,对dbp和sbp有显著因果效应的基因在抗原加工递呈和蛋白重折叠途径中富集,而具有显著水平多效性效应的基因在各代谢过程和蛋白质丰富输出中富集。
最后,mopmr-egger同时具备很高的计算效率,计算时间和物理内存需求与现有的twas方法相似(表2)。
讨论
本发明提出了twas分析的mopmr-egger方法,该方法扩展了单性状pmr-egger到多性状联合分析。mopmr-egger考虑了多个性状之间的相关结构,利用了所有ld相关的cis-snps,检验和控制水平多效性效应,并在似然框架下完成推断。在模拟和真实数据应用中,mopmr-egger均能得到稳定的p值,且大大提高了现有单性状twas方法的检验效能。
mopmr-egger的重要的建模假设是,snps在同一性状上表现出相同的水平多效性效应,该假设直接遵循了egger回归假设,类似于通常用于罕见变异关联分析的负荷效应大小假设。与之前的研究一致,发现,在mopmr-egger中采用的这种假设对于因果效应的估计和检验是相当稳健的。然而,必须充分认识到,这种等水平多效性假设在许多情况下可能过于严格。因此,尽管认为mopmr-egger是实现多性状联合分析的重要第一步,但在未来对水平多效性采用更现实的建模假设是必要的。
主要阐述了mopmr-egger在分析个体水平数据方面的优势。mopmr-egger可以很容易地扩展到对汇总统计量数据分析中(详见材料和方法部分)。具体来讲,基于汇总统计量的mopmr-egger需要基因表达和多结局性状的边际snps效应大小估计及其标准误,cis-snps间的ld相关矩阵,这个矩阵可以根据参考数据集构建。此外,还需要多个性状间相关矩阵的估计。利用每个性状的全基因组snps的边际z得分统计量,可以很容易地估计性状间相关矩阵:因为两个性状之间的相关性约等于两个性状零假设下边际z得分统计量之间相关性。因而,对于每个性状,可以选择p值大于预先设定的显著性阈值(例如10-5)的snps,使用这些边际z得分统计量间的相关性作为性状间相关矩阵的估计。在模拟中验证了基于汇总统计量的mopmr-egger基于个体水平数据的mopmr-egger的拟合结果基本一致,这大大增加了mopmr-egger的适用范围。基于个体水平和汇总统计量水平的mopmr-egger的详细算法见表3,4。
表1在bonferroni多重校正阈值下,英国生物库中五类性状的显著基因数
表2在英国生物样本库五个类别中twas分析时每个基因的平均cpu时间和内存使用
计算是在intelxeone5-2697v3的单线程上进行的。表中列出的计算时间和内存使用情况15,810个基因的平均值。
表3算法1:基于个体水平数据的mopmr-egger,应用r包pmr中的mopmr_individual函数。
表4算法2:基于汇总统计量数据的mopmr-egger,应用r包pmr中的mopmr_summary函数。
应注意的是,以上实例仅用于说明本发明的技术方案而非对其进行限制。尽管参照所给出的实例对本发明进行了详细说明,但是本领域的普通技术人员可根据需要对本发明的技术方案进行修改或者等同替换,而不脱离本发明技术方案的精神和范围。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



