三维植物细胞柔性表面几何建模方法及模型与流程

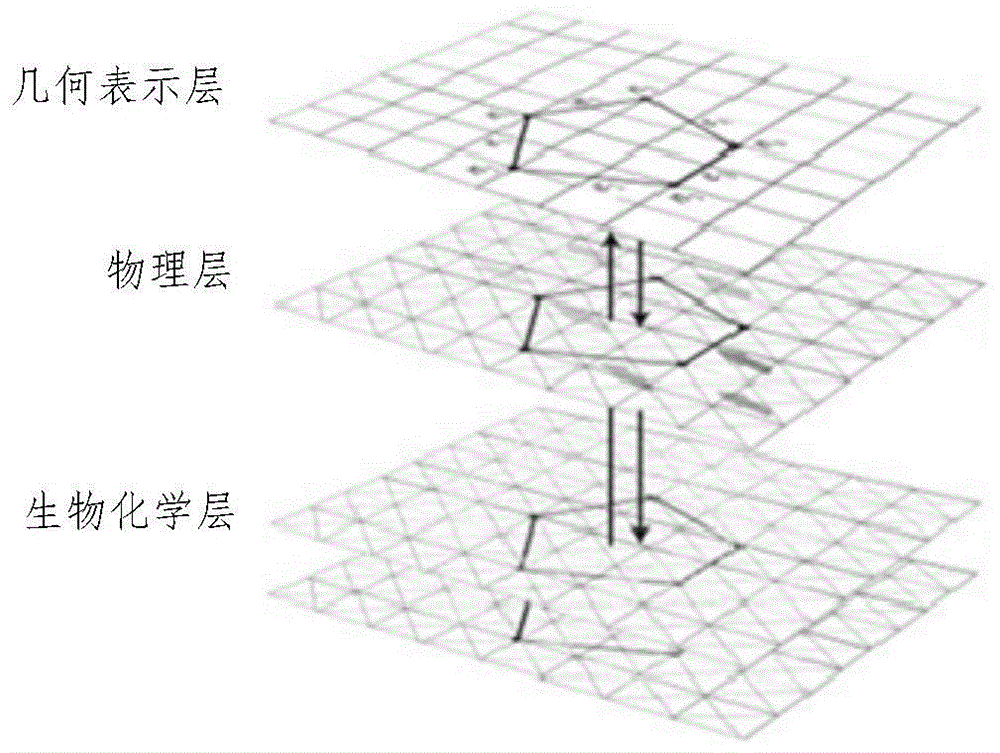
本发明属于生物信息技术领域，具体涉及一种三维植物细胞柔性表面几何建模方法及模型。

背景技术：

生物器官或组织形态建成建模的研究，动物比植物起步较早，在利用几何描述有机体形态方面，英国数学生物学家汤普森于1917年首次出版《生长和形态》，在他的著作中阐述了动物形状的尺度以及类似肥皂薄膜结构(例如：细胞)的表面张力，并运用“汤普森转换法”在笛卡尔网格展示动物头骨的几何形状，这种方法虽然涉及有机体发育初始期和成熟期形态，但忽略新器官形成和分化，这种局限性一直沿续到上世纪60年代末才得以解决。在反应-扩散理论方面，采用数学方法来表示化学物质从初始均匀、稳定的状态再到其从高浓度至低浓度自发形成图案的过程。该理论1952年由著名英国计算机科学家图灵提出，他建立一系列反应扩散微分方程来试图解释自然界有机体的形态建成。格恩赫和迈因哈特借助“反应-扩散”理论并采用短距离激活和长距离抑制的方式来识别激活物、抑制物浓度和源的密度，当源的密度缓慢变化时，激活物和抑制物浓度可以迅速形成图案。中兴大学廖思善借助反应扩散理论研究得到了花豹斑纹专属的方程。也有研究表明模式图案与它们鲁棒性可以对生物形态形成产生重要影响，证实了利用偏微分方程在形态发生研究中具有持久效用特点，但是上述这些模型只是模拟了形态形成的现象，即外在形态的表象，而很少涉及由于生物特征影响该现象的背后机制。

植物组织生长和形态变化起因于复杂动力学，借助计算机模型能够帮助人们较好地理解该过程以及预测它的演化，其可视化建模能直观表达研究对象内在机理与其表象的联系，越来越受到生物研究工作者的青睐。近年来国外在生物形态微观计算机建模的研究进展主要包括以下几个方面：

(1)细胞自动机模型

为实现对大自然中的生物系统模拟，设计繁殖自己的机器，vonneumann提出自我复制自动机理论。起初，vonneumann建立的元胞自动机模型极其复杂，它包含数千个二维的元胞，每一个元胞由29个状态构成，采用的规则具有通用计算性质，它的计算复杂度是现有计算机无法满足。为了解决特定领域问题，其他学者在vonneumann的研究基础上对元胞状态及规则演化方面进行了简化，例如：使用8种状态的元胞自动机开展在计算机虚拟环境中创造人工生命的研究；为了从最简单的规则来观察复杂事物的形成过程，设计了一个类似象棋的二维方形网格，每个方格是一个包含两种状态(“存活”、“死亡”)的“生命游戏”；一维元胞自动机，也称为初等元胞自动机，他的研究表明通过一些简单规则可以完成复杂的系统涌现等；不同遗传算法来提高细胞自动机建模精度。这些模型可以用在模拟不同生长形式的两种植物间的交互等方面。

(2)细胞potts模型

它是基于网络的模型，其目的是将元胞，即生物形态分解的最小单元，定义为相邻晶格点的并集来合成生物形状，该模型是基于哈密尔顿能量函数，通过更新晶格中spin的位置来使能量最小化从而达到稳定。具体应用有：通过potts模型来描述内皮细胞迁移、生长、分裂、细胞粘附和基质结构的演变；借助potts模型来描述早期肾脏发育中简单的管状分支，来研究分支形态是如何依赖于不同的物理或化学因素；采用potts模型对细胞表面张力和元胞粘附性进行了模拟。

(3)粒子模型

在该模型中每个单元由空间中的一个点和一个或多个参数表示，这些参数表示以该点为中心的椭球的半径(或主轴)。生物组织细胞间的相互作用被为具有势函数的软椭球体模拟。具体应用有：基于观察器官样本生长和裂变，建立了可变形上皮组织层的计算模型。与细胞potts模型相比，粒子模型具有更强的物理动机，可以很自然地推广到三维空间，但它们缺乏对细胞形状的明确描述。

(4)椭球体模型

该模型的构建模块是单个单元格，并给定每个单元格特定属性值，这些属性对于所有单元格不一定相同，其中基本属性是单元格受到的可以变形力(拉伸或压缩)来维持其体积，从而对其它单元格产生积极的动力。具体应用有：在生物物理模型研究时空中来模拟其二维肿瘤单层和三维肿瘤球体的生长动力学。

(5)顶点模型

在该模型中形态几何单元是由多边形或多面体表示。生物形状随时间的变化是由二维或三维空间中点的运动所驱动的，这些点被定义为顶点。具体应用：顶点模型用于研究细胞上皮细胞包括细胞运动、粘附、有丝分裂和分层过程。

国内在生物形态微观计算机建模的研究主要是把植物生长建模分成宏观模型与微观模型，前者研究人员一般将植物生物过程抽象一个黑箱，再利用统计回归、机器学习等方法建立其输入与输出关系的数学模型，这些模型能够宏观地反应植物生长规律并对其生长过程进行检验与预测。然而如何揭示植物生物内在机理，进一步提升其模型的科学与应用价值，需要科研人员建立细胞、分子和基因尺度的微观模型。国内对植物宏观建模研究起步较早，而对其微观建模研究鲜有报道。

使用上述建模方法虽然能够实现细胞二维形状或三维细胞拓扑结构，但是无法实现植物细胞属于超柔性三维几何对象。基于此，本发明提出的拓扑与曲面组合方法不仅能够表示细胞形状的拓扑，而且还能表达细胞柔性变形中的丰富几何信息。

技术实现要素：

为了解决上述技术问题，本发明提供了一种三维植物细胞柔性表面几何建模方法及模型。

本发明的目的是提供一种三维植物细胞柔性表面几何建模方法，包括以下步骤：

采用n维广义映射建立细胞柔性形状拓扑模型；

采用b样条曲面对细胞形状几何细胞描述；

设计几何顶、边与面的查询来定位需要进行柔性变形的几何对象：分别创建dart、edge与face拓扑单元的数据结构，其中dart的数据结构包括9个分量，前四个分量alpha0-alpha3为细胞形状拓扑缝合操作；第五个分量关联到边拓扑，一条拓扑边应对多个dart数据结构；第六个分量为dart的标识编号；第七个分量为dart嵌入到欧式空间点的坐标；第八个分量对应b样条曲面的控制网格顶点；最后一个分量为颜色值；边、面拓扑单元数据结构分别定义在edge与face拓扑单元中，一个面单元由若干条边单元组成，一条边指向多个面单元。

优选的，上述三维植物细胞柔性表面几何建模方法，采用n维广义映射建立细胞柔性形状拓扑模型具体过程如下：将细胞形状自顶向下分解成体积、面、边、点的几何形状要素；然后，以“dart”为最小拓扑单元，从下而上组合细胞形状的整体拓扑结构，并为其设计相应的检索算法。

优选的，上述三维植物细胞柔性表面几何建模方法，相应的检索算法为：设2-gmaps是定义一个集合s上的一组操作:g＝(s，α0，α1，α2)，其中该集合由一些dart单元di构成；

在零维拓扑空间中每个di有n+1个α操作；在零维拓扑空间操作α0～α2都没有对di拓扑单元缝合di指定自身，则称di为固定点，即<αi>(di)＝di；在一维拓扑空间这三个操作对每两个di、di+1进行缝合形成边拓扑单元，即对合操作，<α1>(di)＝(di)表示该拓扑单元的边界；

在二维拓扑空间能够将一维边拓扑单元提升到二维拓扑空间。

优选的，上述三维植物细胞柔性表面几何建模方法，参照上述算法递推可获得到n-gmaps操作定义对全部最少单元dart进行组合操作，其中0≤i≤i+2≤j≤3。

优选的，上述三维植物细胞柔性表面几何建模方法，采用b样条曲面对细胞形状几何细胞描述所用b样条曲线公式如下：

其中，pi为b样条曲线的控制顶点，n为控制顶点的个数，ni,k表示k次b样条基函数，通常其基函数由u个非递减节点矢量代入cox-deboor递推公式生成。

优选的，上述三维植物细胞柔性表面几何建模方法，所用b样条曲面计算公式如下：

其中，控制曲面网格多边形大小为m×n，pi,j表示第i行与第j列控制顶点，u,v分别表示曲面两个方向的节点矢量，ni,k(u)、nj,k(v)分别为u,v方向的k次b样条基函数。

优选的，上述三维植物细胞柔性表面几何建模方法，采用增加节点矢量来解决三次b样条曲线曲面过控制多边形和网格端点插值。

优选的，上述三维植物细胞柔性表面几何建模方法，给定一条三次b样条，4个控制顶点，可得共需要8个节点矢量，其中u0＝u1＝u2＝0,u5＝u6＝u7可获得一条顶点p0与p3的b样条曲线。

优选的，上述三维植物细胞柔性表面几何建模方法，三次b样条曲面共16个控制顶点，64个矢量节点，全部边界点对应三个重复节点矢量，控制网络内部点对应一个重复节点矢量。

与现有技术相比，本发明提供的三维植物细胞柔性表面几何建模方法及模型，具有以下有益效果：

1、植物不仅具有丰富多样的外部形态结构，而且有着极及复杂的生理过程和其功能表达。随着生命科学、认知科学与信息科学的进一步交叉，为了实现植物形态结构的精确描述与分析，本发明通过计算机技术将复杂结构和功能进行虚拟化，在柔性植物形态建模与计算机仿真方面重点进行研究分析，以此来表示虚拟环境中的内容。本发明提出的拓扑与曲面组合方法不仅能够表示细胞形状的拓扑，而且还能表达细胞变形丰富的柔性几何信息。所建模型的查询功能可以精确定位细胞形状的某个几何片元，从而可以自由地对该片元进一步进行应力与应变分析。该研究内容不但处于当前的研究前沿，而且还会成为未来一段时间的研究热点。

2、本发明采用n-维广义映射理论，首先将细胞形状自顶向下分解成体积、面、边、点等几何形状要素；然后，以“dart”为最小拓扑单元，从下而上组合细胞形状的整体拓扑结构，并为其设计相应的检索算法；再其次结合曲线、曲线能够几何细节与易控制变形的优点进行细胞形状的几何建模；最后，通过c++语言与opengl图形库进行程序实现上述过程。其优点有：

(1)采用拓扑方法的植物细胞几何形状建模，用户不仅能够自由地查询几何模型的任意单元，而且在程序中实现了查询结果的高亮显示，为细胞形状变形的弹性力学建模过程，提供细胞形状的边界自动化检索；

(2)使用n维广义映射能够用统一方式描述植物细胞形状的拓扑，它对后期的模型维护很方便；

(3)b样条曲面来描述细胞几何细节，有助于引入物理受力变形的分析。

3、本发明采用的拓扑方法属于边界表示法的一种，half-edge数据结构也是作为一个流行的边界表示法，后者虽然数据结构实现简单，但是它关联信息过于复杂、维护成本高，例如，当细胞拓扑网络发生变化时，需要更新大量的指针操作。本发明采用的方法具有统一的数据结构，通过拓扑组合操作有利于降低建模与模型维护成本。

附图说明

图1为本发明三维植物细胞柔性表面几何建模方法的立体结构示意图；

图2为细胞表面形状拓扑结构；

(a)上表面；(b)侧面；

图3为植物细胞上表面拓扑结构分解过程；

(a)二维的cycle拓扑；(b)一维的拓扑边；(c)零维的拓扑顶点；

图4为图3的上表面的序拓扑关系图；

图5为n-gmaps组合操作；

(a)dart单元di；(b)n-gmaps组合；

图6为有效节点矢量与控制点；

(a)b样条曲线；(b)b样条曲面；

图7为插值后有效节点矢量与控制点；

(a)b样条曲线；(b)b样条曲面；

图8为三维细胞拓扑几何模型数据结构；

图9为三维细胞形状拓扑效果；

(a)顶视图；(b)任意解度；

图10为本发明建立的三维细胞几何结构；

(a)三维细胞俯视图；(b)三维细胞变形效果图；

图11为细胞的几何形状查询操作及仿真；

(a)细胞几何图形顶点查询结果；(b)细胞图形边的查询结果；(c)细胞几何图形面查询结果。

具体实施方式

为了使本领域技术人员更好地理解本发明的技术方案能予以实施，下面结合具体实施例和附图对本发明作进一步说明。

植物细胞在半透的细胞膜外比动物细胞多一个“坚硬”的细胞壁，它是一个两边通透的网状结构。当细胞内外物质发生反应扩散时，会导致细胞膜两侧物质浓度的改变，小分子(例如：水分子)从低浓度的溶液穿过细胞膜进入高浓度溶液中，细胞内物质的增多会导致其体积膨胀，细胞壁产生一个反作用力来保护细胞膜不破裂；如果小分子流出细胞，由其体积收缩产生质壁分离。因此，植物细胞是一个超柔性几何对象，其生长形态的改变是时间与空间的函数，如图1所示，它是一个自底向上经历生物化学层、物理层和几何表示三层的交互过程。当细胞受下层信号驱动时其形状发生膨胀或收缩变形时，其几何边缘点间拓扑关系不发生改变。

不失一般性，我们可以假设植物细胞形状是五边形棱柱体结构，如图2所示，细胞壁上表、侧面形状拓分别是由{a,b,c,d,e}顶点集合与{a,b,f,g}顶点集合上建立的拓扑关系组合，其中en，n＝1～5表示顶点间拓扑边单元。

基于此本发明实施例1提出一种基于拓扑与曲面组合的三维植物细胞几何建模方法。

实施例1

本实施例提出一种细胞形状的拓扑结构与曲面造型相结合的三维几何建模技术。包括以下步骤：

步骤1，采用n维广义映射建立细胞柔性形状拓扑模型

在植物细胞形状拓扑方面将细胞形状结构分解不同n维空间的拓扑单元，如图3所示，二维细胞上表面拓扑cycle单元从左到右分解成5条一维的拓扑边，每条拓扑边分解成零维的拓扑点单元。

在细胞形状拓扑分解过程中，不仅需要得到不同维度上的拓扑，而且还需要存储不同维度上的拓扑关系，如图4所示，细胞上表面的分解单元的序拓扑关系。同理容易获得整个三维细胞形状的拓扑单元与其序拓扑关系。

三维细胞形状拓扑建模是指建立在零维度的最小拓扑单元集与序拓扑关系还原到整个细胞拓扑结构，换句话来讲这些拓扑单元能够定义统一的数据结构，只要给定它们任意维度的序拓扑关系图就可以还原任意维度的拓扑结构。由于还原是一个自动化的过程。

本实施例引入了n维广义映射(n-dimensionalgeneralizedmaps,n-gmaps)来限定这些最小单元还原过程，该理论由lienhardt(lienhardtp.topologicalmodelsforboundaryrepresentation:acomparisonwithn-dimensionalgeneralizedmaps[j].computer-aideddesign,1991,23(11):59-82.)在组合映射(combinatorialmaps)的基础上提出来的边界表示方法，这些最小单元称作dart。这里给出了二维拓扑空间还原操作定义，设2-gmaps是定义一个集合s上的一组操作:g＝(s，α0，α1，α2)，其中该集合由一些dart单元di构成，如图5(a)所示，在零维拓扑空间中每个di有n+1个α操作。在零维拓扑空间操作α0～α2都没有对di拓扑单元缝合di指定自身，则称di为固定点，即<αi>(di)＝di；在一维拓扑空间这三个操作对每两个di、di+1进行缝合形成边拓扑单元，即对合(involution)操作，<α1>(di)＝(di)表示该拓扑单元的边界；参见图5(b)，在二维拓扑空间能够将一维边拓扑单元提升到二维拓扑空间，以此递推可获得到n-gmaps操作定义对全部最少单元dart进行组合操作，其中0≤i≤i+2≤j≤3。

步骤2，采用b样条曲面对细胞形状几何细胞描述

借助n维广义映射能够很好的解决细胞形状的拓扑模型建立，然而所得细胞拓扑模型丢失了其表面变形的几何细节，导致无法表示受力柔性变形形状。本实施例用有理b样条曲线、曲面来建立对象形状模型，其表达式如公式(1)与公式(2)所示。

其中，pi为b样条曲线的控制顶点，n为控制顶点的个数，ni,k表示k次b样条基函数，通常其基函数由u个非递减节点矢量代入cox-deboor递推公式生成。同理可获得b样条曲面计算公式：

其中，控制曲面网格多边形大小为m×n，pi,j表示第i行与第j列控制顶点，u,v分别表示曲面两个方向的节点矢量，ni,k(u)、nj,k(v)分别为u,v方向的k次b样条基函数。由于b样条曲线曲线不会在控制端点插值，如图6(a)所示，一条三次的b样条曲线，在四个等距离的节点向量u，b样条曲线不过p0与p3，插值点只在p1与p2，图6(b)三次b样条曲面也出现了该问题，从而导致b样条曲面不能与细胞形状拓扑模型精确组合。

针对上述问题，本实施例采用增加节点矢量来解决三次b样条曲线曲面过控制多边形和网格端点插值。如图7(a)所示，给定一条三次b样条，4个控制顶点，可得共需要8个节点矢量，其中u0＝u1＝u2＝0,u5＝u6＝u7可获得一条顶点p0与p3的b样条曲线，同理三次b样条曲面共16个控制顶点，64个矢量节点，控制网格的边界插值的节点矢量设置如图7(b)所示，全部边界点对应三个重复节点矢量，控制网络内部点对应一个重复节点矢量。

步骤3，设计几何顶、边与面的查询来定位需要进行柔性变形的几何对象

植物细胞三维几何形状模型的数据结构描述，如图8所示，分别创建dart、edge与face拓扑单元的数据结构，其中dart的数据结构包括9个分量，前四个分量alpha0-alpha3为细胞形状拓扑缝合操作；第五个分量关联到边拓扑，一条拓扑边应对多个dart数据结构；第六个分量为dart的标识编号；第七个分量为dart嵌入到欧式空间点的坐标；第八个分量对应b样条曲面的控制网格顶点(包括欧式空间的坐标)；最后一个分量为颜色值(包括红、绿、蓝和透明度四个分量)。边、面拓扑单元数据结构分别定义在edge与face中，一个面单元由若干条边单元组成，一条边指向多个面单元。

通过上述方法构建出了能够展示细胞柔性几何细节的模型，图9为三维细胞形状拓扑效果；(a)顶视图；(b)任意解度；图10本发明建立的三维细胞几何结构，(a)三维细胞俯视图；(b)三维细胞变形效果图。

利用上述模型可从顶点、边、面三个层次查询细胞几何形状，也可以通过修改曲面控制点的坐标来更新曲面形状。所建模型的查询功能可以精确定位细胞形状的某个几何片元，从而可以自由地对该片元进一步进行应力与应变分析，达到模拟细胞受力后其柔性几何形状的变化效果。

图11为细胞的几何形状查询操作及仿真；图11(a)顶点，其对应的查询过程如下：

图11(b)边；对应的查询过程如下：

图11(c)面；对应的查询过程如下：

需要说明的是，本发明中涉及数值范围时，应理解为每个数值范围的两个端点以及两个端点之间任何一个数值均可选用，由于采用的步骤方法与实施例相同，为了防止赘述，本发明描述了优选的实施例。尽管已描述了本发明的优选实施例，但本领域内的技术人员一旦得知了基本创造性概念，则可对这些实施例做出另外的变更和修改。所以，所附权利要求意欲解释为包括优选实施例以及落入本发明范围的所有变更和修改。

显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除