基于数据驱动多组元镍基高温合金γ`相演化的预测方法与流程

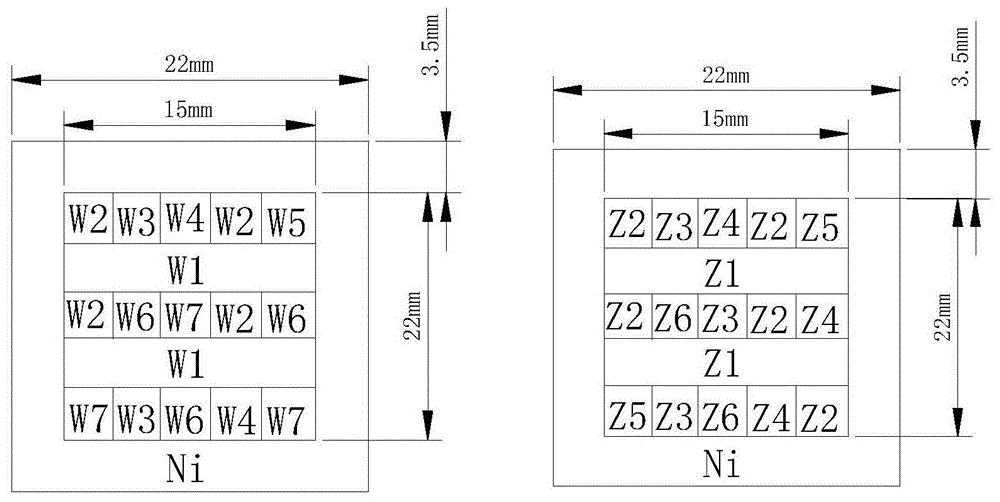
本发明涉及多组元合金互扩散领域，更具体地，涉及一种基于数据驱动多组元镍基高温合金γ’相演化的预测方法。

背景技术：

镍基高温合金主要用于航空发动机涡轮盘、涡轮叶片等热端部件。从上世纪40年代开始，航空发动机涡轮盘和涡轮叶片的涡轮进口温度、推重比不断提高，对高温合金在高温长期服役条件下的组织稳定性提出了更高的要求。在长期高温服役条件下，镍基高温合金中的γ’相会逐渐长大，导致合金的力学性能恶化。因此，微观组织稳定性对高温合金的服役性能具有重要影响。一般通过实验的方法研究微观组织稳定性主要是通过长期的热暴露实验，该实验的周期较长、成本较高。而通过理论计算的方法预测γ’相的粗化速率对加速镍基高温合金的成分设计与优化具有至关重要的作用。

镍基合金的维管组织稳定性、氧化、蠕变等性能与合金化元素的互扩散系数紧密相关，而镍基高温合金化学成分多(＞7个)，合金元素之间的交互作用比较复杂，当前镍基高温合金的互扩散系数研究主要集中在二元、三元等低组分体系，对镍基多组分体系的互扩散系数主要是基于低组分体系的互扩散信息通过caphad方法外推得到，与实际合金的互扩散行为具有较大的偏差，因此，通过实验的方法高通量获得可靠的镍基多组分原子移动性数据库对预测γ’相的演化以及通过相场模拟方法研究镍基微结构的演化具有至关重要的作用。

合金的微观组织演化、蠕变、氧化等过程均涉及合金元素的扩散过程，通常使用互扩散系数来描述合金化元素在某个特定的相中的扩散的快慢。目前，镍基多组分体系的互扩散系数在文献中鲜有报道，导致合金设计过程中依赖二元、三元等低组分体系的扩散信息，未考虑到元素之间的相互作用，且外推得到的多组分扩散动力学数据库的可靠性有待考量，对合金设计的可靠性提出了挑战。

互扩散系数作为一种物理性质，不能通过实验直接获得，而是需要通过求解fick第二定律或einstein-smoluchowski方程来获得。互扩散系数的测定方法主要有理论计算与实验测定。理论计算主要是结合第一性原理计算、集团展开法和蒙特卡罗等方法来获得互扩散系数。实验测定的方法主要是基于fick第二定律从扩散偶的成分-距离曲线中提取互扩散系数，其中最为广泛使用的是通过固相扩散偶方法来获得成分-距离曲线，进而发展为扩散多元节方法。从成分-距离曲线中提取互扩散系数的传统方法有boltzmann-matano方法、sauer-freise方法、wagner方法和kirkaldy-matano方法等，而这些方法只适合求解二元、三元合金体系的互扩散系数，难以求解多组元合金体系互扩散系数。

镍基高温合金在长期高温服役条件下，由于表面能的降低，γ’相会逐渐长大，降低合金的力学性能。大量研究表明，γ’相的粗化是体扩散控制的过程。根据经典的lsw粗化理论可知，γ’相的粗化速率与合金化元素在基体相中的扩散紧密相关。目前在计算合金基体相中有效扩散系数时，采用的是镍基二元体系的自扩散系数或杂质扩散系数与合金中元素的摩尔分数乘积的线性叠加来获得，未考虑粗话过程中元素之间的交互作用。

为进一步计算多组元镍基高温合金中元素的互扩散系数，通过已有的镍基低组分体系的互扩散信息，采用calphad方法外推得到多组分镍基高温合金的互扩散系数是一个重要的计算方法，如商用的dictra软件中的mobni2数据库。但该方法的缺点是未考虑多组分合金中元素复杂的交互作用，且一些关键的低组分体系实验数据难以通过试验获得。在模拟镍基高温合金γ’相演化时如商用的pandat、jmatpro等软件均采用镍基二元体系的自扩散系数或杂质扩散系数。然而，镍基高温合金组分众多，元素交互作用较为复杂，采用二元体系的自扩散系数或杂质扩散系数计算镍基合金的有效扩散系数时未考虑到元素之间复杂的交互作用。

技术实现要素：

基于现有技术中存在的上述技术问题，本发明提供了一种预测多组元镍基高温合金γ’相演化的预测方法，该方法先通过多组元合金扩散偶获得扩散偶的成分-距离曲线，通过该成分距离曲线获得可靠的多组分镍基高温合金基体相原子移动性数据库，再结合γ’相的lsw粗化规律预测多组元镍基高温合金在时效过程中γ’相的粗化速率常数、粗化激活能等，该方法可有效、可靠、快速地获得多组元镍基高温合金基体相的原子移动性数据库，并应用于预测γ’相的演化，促进相关理论和应用的发展。

为实现上述目的，本发明的技术方案如下：

一种基于数据驱动多组元镍基高温合金γ’相演化的预测方法，包括以下步骤：

s1：通过合金扩散多元节技术高通量制备若干组多组元镍基高温合金扩散偶；

s2：通过检测仪器检测获得每组所述扩散偶的成分-距离曲线；

s3：根据所述步骤s2获得的成分-距离曲线，建立多组元镍基高温合金互扩散系数矩阵，具体操作步骤如下：

s3-1：通过步骤s2获得的成分-距离曲线以及现有技术中已评估的镍基二元体系的自扩散系数或杂质扩散系数的原子移动性参数mk，对于现有技术中未记载的镍基二元体系的原子移动性参数进行近似处理，将二元交互作用参数作为可调整的参数，设为常数a；

s3-2：根据多组元合金互扩散系数与原子移动性参数存在的下述关系，其表达式如下：

式1中：i、j、k表示不同元素，n表示溶剂ni,r为气体常数，t为扩散退火温度，mi为原子移动性参数，xi表示元素i的摩尔分数，是热力学因子；当i和j是同一个元素时，热力学因子等于1，否则等于0；

s3-3根据fick第二定律，n元系中元素互扩散系数与所述成分-距离曲线存在下述关系，其表达式如下：

式2中：ci为元素i的成分，t为退火时间，x为距离，为多组元合金互扩散系数；

s3-4通过所述步骤s3-1、s3-2、s3-3过程可以初步模拟出扩散偶的成分-距离曲线，并与实验的成分-距离曲线对比，为了获得最可靠的原子移动性参数，采用遗传算法不断迭代优化调整参数a，直至模拟的成分-距离曲线与实验的成分-距离曲线在可以接受的误差范围内，所获得的原子移动性参数为当前的原子性数据库；其中，采用遗传算法优化调整参数a的过程通过hitdic软件实现；

s4：验证所述原子移动性数据库的可靠性；

s5：通过所述原子移动性数据库，结合γ’相的lsw粗化规律，预测多组元镍基高温合金在时效过程中γ’相的粗化速率常数k和粗化激活能qeff，其具体表达式如下：

式3-6中，d0,eff为有效指数前因子值，ci为元素i的摩尔分数，d^*o,i为所述原子移动性数据库计算的i元素在基体相中的示踪扩散指数前因子值，qeff为粗化激活能，q^*i为所述原子移动性数据库计算的i元素在基体相中的示踪扩散激活能，deff为有效扩散系数，r为气体常数，t为时效温度，k为粗化速率常数，σ为γ/γ′相界面能，nα为溶质元素在基体相中的摩尔分数，vm为γ′相的摩尔体积。

在一些实施方式中，所述s2中，检测所述扩散偶时，检测距离为3000μm或4000μm。

在一些实施方式中，所述检测仪器为微束x射线荧光设备。

在一些实施方式中，所述检测仪器对所述扩散偶的检测参数为：束斑为15μm，信息深度为10μm，能量分辨率为130ev，检测速率为5s/point。

在一些实施方式中，所述高通量制备若干组扩散偶的方法包括以下步骤：

步骤一、根据待研究的合金成分空间，进行合金和组合设计；

步骤二、熔炼若干个多组元合金块并根据组合设计将所述合金块排列布置形成一个合金块整体；

步骤三、将所述合金块整体进行加工、打磨；

步骤四、制作纯镍包套和包套盖，将经步骤三处理后的合金块整体装配到所述包套中，然后将包套与包套盖焊接成一体，确保包套内部为真空状态，形成合金扩散偶试样；

步骤五、对所述合金扩散偶试样采用热等静压，使合金块整体中各合金块之间、各合金块与包套之间形成良好的界面结合；其中，所述热等静压温度为1180℃，压力为150mpa，时间为8h；

步骤六、经步骤五处理后的合金扩散偶试样在1180℃或1280℃下进行扩散退火处理；

步骤七、经步骤六处理后的合金扩散偶试样进行镶样与制样，用于后续检测获得扩散偶的成分-距离曲线。

相较于现有技术，本发明的有益效果如下：

1.采用合金扩散多元节技术高通量制备多组元高温合金扩散偶，可快速获得多组元高温合金扩散偶，无需使用多次实验，大大减少工作量；

2.利用有效的多组元高温合金扩散偶，获得扩散偶的成分-距离曲线，然后将原子二元交互作用参数作为可调整的参数，设为常数a，为了获得最可靠的原子移动性参数，采用遗传算法不断迭代优化调整参数a，直至模拟的成分-距离曲线与实验的成分-距离曲线在可接受的误差范围内，从而获得基于数据驱动多组元镍基高温合金原子移动性数据库；结合γ’相的lsw粗化规律，预测镍基高温合金在时效过程中γ’相的演化，通过结合公开文献的实验数据证实本发明可对镍基高温合金的γ’相演化如粗化激活能、粗化速率常数进行可靠的预测，从而可预测合金化学成分较多(＞4)的多组元高温合金中γ’相的演化，而且准确度高，在设计合金时可依据通过本发明预测的时效温度的粗化激活能和粗化速率常数进行成分设计，有利于促进相关理论和应用的发展。

附图说明

图1为具体实施例中多组元合金的结构设计图；

图2为具体实施例中的高通量制备多组元合金扩散偶的制备流程图。

图3为本发明所提供的部分成分-距离曲线模拟值与实验值对比结果。

图4为本发明所提供的原子移动性数据库对镍基三元体系互扩散系数的预测值与相关文献中所记载的实验值对比结果。

图5和图6分别为本发明所提供的预测方法对镍基高温合金γ’相的粗化激活能和粗化速率常数的预测值与文献中所记载的实验值对比结果。

具体实施方式

在下面的描述中阐述了很多具体细节以便于充分理解本发明。但是本发明能够以很多不同于在此描述的其它方式来实施，本领域技术人员可以在不违背本发明内涵的情况下做类似改进，因此本发明不受下面公开的具体实施的限制。

除非另有定义，本文所使用的所有的技术和科学术语与属于本发明的技术领域的技术人员通常理解的含义相同。本文中在本发明的说明书中所使用的术语只是为了描述具体的实施例的目的，不是旨在于限制本发明。

实施例1

一种基于数据驱动多组元镍基高温合金γ’相演化的预测方法，包括以下步骤：

s1：通过合金扩散多元节技术高通量制备若干组多组元镍基高温合金扩散偶；

s2：通过检测仪器检测获得每组所述扩散偶的成分-距离曲线；

s3：根据所述步骤s2获得的成分-距离曲线，建立多组元镍基高温合金互扩散系数矩阵，具体操作步骤如下：

s3-1：通过步骤s2获得的成分-距离曲线以及现有技术中已评估的镍基二元体系的自扩散系数或杂质扩散系数的原子移动性参数mk，对于现有技术中未记载的镍基二元体系的原子移动性参数进行近似处理，将二元交互作用作为可调整的参数，设为常数a；

s3-2：根据多组元合金互扩散系数与原子移动性参数存在的下述关系，其表达式如下：

式1中：i、j、k表示不同元素，n表示溶剂ni,r为气体常数，t为扩散退火温度，mi为原子移动性参数，xi表示元素i的摩尔分数，是热力学因子；当i和j是同一个元素时，热力学因子等于1，否则等于0；

s3-3：根据fick第二定律，n元系中元素互扩散系数与所述成分-距离曲线存在下述关系，其表达式如下：

式2中：n为多组元合金中金属元素数量，n为溶剂ni，i＝1，2，…，n-1表示第1个元素，第2个元素，…，第n-1个元素；ci为元素i的成分，t为退火时间，x为距离，为多组元合金互扩散系数；

s3-4：通过所述步骤s3-1、s3-2、s3-3过程初步模拟出扩散偶的成分-距离曲线，并与实验的成分-距离曲线对比，为了获得最可靠的原子移动性参数，采用遗传算法不断迭代优化调整参数a，直至模拟的成分-距离曲线与实验的成分-距离曲线在可以接受的误差范围内，所获得的原子移动性参数为当前的原子性数据库；其中，采用遗传算法优化调整参数a的过程通过hitdic软件实现；

s4：验证所述原子移动性数据库的可靠性；

s5：通过所述原子移动性数据库，结合γ’相的lsw粗化规律，预测镍基高温合金在时效过程中γ’相的粗化速率常数k和粗化激活能qeff等，其表达式如下：

式3-6中，d0,eff为有效指数前因子值，ci为元素i的摩尔分数，d^*o,i为所述原子移动性数据库计算的i元素在基体相中的示踪扩散指数前因子值，qeff为粗化激活能，q^*i为所述原子移动性数据库计算的i元素在基体相中的示踪扩散激活能，deff为有效扩散系数，r为气体常数，t为时效温度，k为粗化速率常数，σ为γ/γ′相界面能，nα为溶质元素在基体相中的摩尔分数，vm为γ′相的摩尔体积。

以下结合具体的操作方式对本发明进行详细地说明：

一、多组元镍基高温合金扩散偶的高通量制备，具体步骤如下：

步骤一：根据待研究的合金成分空间，进行镍基多组元合金扩散偶结构设计，本实施例的合金扩散偶结构如图1所示；

步骤二：根据图1的结构设计图(其中左图为w系列合金设计结构，右图为z系列合金设计结构)和图2的加工工艺流程图以及表1的合金组分，熔炼相应的合金块，然后将合金块设计的结构进行排列布置形成一个合金块整体；

步骤三：对步骤二所形成的合金块整体进行加工、打磨；

步骤四：制作纯镍包套和包套盖，将经步骤三处理后的合金块整体装配到所述包套中，然后将包套与包套盖焊接成一体，确保包套内部为真空状态，形成合金扩散偶试样；

步骤五：对所述合金扩散偶试样采用高温热等静压，使合金块整体中各合金块之间、各合金块与包套之间形成良好的界面结合；其中，所述热等静压温度为1180℃，压力为150mpa，时间为8h；

步骤六：经步骤五处理后的合金扩散偶试样进行扩散退火处理，w系列合金退火温度为1180℃，退火时间为1000h，w系列合金退火温度为1280℃，退火时间为100h，形成扩散成分梯度；

步骤七：经步骤六处理后的合金扩散偶试样，然后进行镶样与制样，用于后续检测获得扩散偶的成分-距离曲线。

表1各合金块的组成成分

二、试样成分-距离曲线的获取

采用微束x射线荧光设备对所制成的试样的扩散偶分别进行检测分析，检测分析距离为：检测w系列扩散偶界面左右两边约3000μm的一段距离的原子扩散情况(以本实施例为具体说明，检测w1和w2之间元素互扩散形成的成分梯度，检测宽度为3000μm或4000μm)，得到所述扩散偶的的成分-距离曲线，具体测试方式如下：

微束x射线荧光设备的检测参数为：束斑为15μm，信息深度为10μm，能量分辨率为130ev，检测速率为5s/point，然后将x射线对准扩散偶界面两侧的一定长度d，检测扩散偶界面两侧的成分梯度，根据检测结果获得实验的成分-距离曲线；同理，测试其他扩散偶的成分距离曲线，如图3。图3中，左图为ni+28co扩散偶的实验-成分距离曲线(散点)与模拟的成分距离曲线(实线)比较；右图为28co+4mo扩散偶的实验成分距离曲线(散点)与模拟的成分距离曲线(实线)比较。由图3可以看出，本方法模拟的成分-距离曲线与实验值具有较好的一致性，证明当前获得的原子移动性数据库是可靠的。

三、根据成分-距离曲线，获得原子移动性数据库，具体步骤如下：

(1)通过成分-距离曲线以及现有技术中(本申请中引用如下述参考文献1-17中的相关数据)已评估的镍基二元体系的自扩散系数或杂质扩散系数的原子移动性参数，对于现有技术中未记载的镍基二元体系的原子移动性参数进行近似处理，将二元交互作用作为可调整的参数，设为常数a；

(2)互扩散系数与原子移动性参数存在下述关系，其表达式如下：

式1中：i、j，k表示不同元素，n表示溶剂ni,r为气体常数，t为扩散退火温度，mi为原子移动性参数，是热力学因子。在当前模型中，当i和j是同一个元素时，热力学因子等于1，否则等于0；

(3)根据fick第二定律，n元系中元素互扩散系数与成分距离曲线存在下述关系，其表达式如下：

式2中：ci为元素i的成分，t为退火时间，x为距离，为互扩散系数；

(4)通过所述步骤(1)、(2)、(3)过程可以初步模拟出扩散偶的成分-距离曲线，并与实验的成分-距离曲线对比，采用遗传算法不断迭代优化调整参数a，直至模拟的成分-距离曲线与实验的成分-距离曲线在可以接受的误差范围内，所获得的原子移动性参数为当前的原子性数据库；其中，采用遗传算法优化调整参数a的过程通过hitdic软件实现。

结合现有相关文献(下述编号为1-17的文献)的相应实验数据结果，确定本发明的原子移动性数据库计算的镍基三元体系互扩散系数与实验结果一致性较高，从而说明当前获得的原子移动性数据库具有较好的可靠性，具体如图4所示。

如图4，图4为本发明所提供的镍基三元系互扩散系数模拟值(实线和虚线)与相关文献中所记载的相应实验值(散点)的对比结果，其中，横坐标为为实验值测定结果，纵坐标为模拟值，虚线为模拟互扩散系数可接受的误差范围。图4中，模拟值均在可接受的误差范围内，说明本发明所提供的原子移动性数据库可靠性高。

其中，图4使用的实验数据来源于以下文献：

1、xug,liuy,kangz.atomicmobilitiesandinterdiffusivitiesforfccni-cr-nballoys[j].metallurgicalandmaterialstransactionsb,2016,47(5):3126–3131.

2、zhun,lij,lux-g,etal.experimentalandcomputationalstudyofdiffusionmobilitiesforfccni-cr-moalloys[j].metallurgicalandmaterialstransactionsa,2015,46(11):5444–5455.

3、wangj,wangy,zhun,etal.experimentalandcomputationalstudyofinterdiffusionforfccni-co-walloys[j].journalofphaseequilibriaanddiffusion,2017,38(1):37–50.

4、chenj,zhangl,zhongj,etal.high-throughputmeasurementofthecomposition-dependentinterdiffusivitymatricesinni-richfccni-al-taalloysatelevatedtemperatures[j].journalofalloysandcompounds,2016,688:320–328.

5、wens,tangy,zhongj,etal.high-throughputmeasurementsofinterdiffusivitymatricesinfacecenteredcubicni–al–moalloysat1273–1473k[j].journalofmaterialsresearch,2017,32(11):2188–2201.

6、wangcp,yux,qinsy,etal.interdiffusionandatomicmobilitiesinfccni-mo-taalloys[j].journalofphaseequilibriaanddiffusion,2019,40(3):432–441.

7、cuipingw,shiyangq,yongl,etal.interdiffusionandatomicmobilitiesinni-richfccni-cr-walloys[j].raremetalmaterialsandengineering,2020:6.

8、cuipingw,yuanjingl,yongl,etal.interdiffusionandatomicmobilitiesinni-richfccni-nb-tialloys[j].raremetalmaterialsandengineering,2019:6.

9、yangyl,shiz,luoys,etal.interdiffusionandatomicmobilitystudiesinni-richfccni-co-alalloys[j].journalofphaseequilibriaanddiffusion,2016,37(3):269–276.

10、wangy,lux-g.interdiffusionanddiffusionmobilityforfccni-co-moalloys[j].journalofphaseequilibriaanddiffusion,2017,38(5):656–664.

11、nesbittja,heckelrw.interdiffusioninni-rich,ni-cr-aialloysat1100and12oo～partii.diffusioncoefficientsandpredictedconcentrationprofiles[j].:12.

12、xug,liuy,kangz.mobilities,interdiffusivitiesandtheirkineticimplicationsforfccni-al-nballoys[j].journalofalloysandcompounds,2017,709:272–276.

13、karunaratnemsa,carterp,reedrc.onthediffusionofaluminiumandtitaniumintheni-richni–al–tisystembetween900and1200℃[j].actamaterialia,2001,49(5):861–875.

14、chenj,zhangl,lux-g.screeningofpossiblere-substitutionalelementsinsingle-crystalni-basedsuperalloys:aviewpointfrominterdiffusioncoefficientsinni-al-xternaries[j].metallurgicalandmaterialstransactionsa,2018,49(7):2999–3010.

15、huangj,wangy,wangj,etal.thermodynamicassessmentsoftheni-cr-tisystemandatomicmobilityofitsfccphase[j].journalofphaseequilibriaanddiffusion,2018,39(5):597–609.

16、wangy,wangj,wangh,etal.thermodynamicdescriptionoftheni-mo-wsystemandinterdiffusionstudyofitsfccphase[j].calphad,2018,61:165–172.

17、林远靖.部分ni基高温合金fcc相互扩散系数的实验测定及扩散动力学计算[j].厦门大学,2018.

四、根据多组分镍基高温合金基体相原子移动性数据库对γ’相演化进行预测

通过获得的成分-距离曲线，基于γ’相的lsw粗化规律，预测镍基高温合金在时效过程中γ’相的粗化速率常数k和粗化激活能qeff，其表达式如下：

式3-6中，d0,eff为有效指数前因子值，ci为元素i的摩尔分数，d^*o,i为所述原子移动性数据库计算的i元素在基体相中的示踪扩散指数前因子值，qeff为粗化激活能，q^*i为所述原子移动性数据库计算的i元素在基体相中的示踪扩散激活能，deff为有效扩散系数，r为气体常数，t为时效温度，k为粗化速率常数，σ为γ/γ′相界面能，nα为溶质元素在基体相中的摩尔分数，vm为γ′相的摩尔体积。

式3-6中，nα和vm参数通过热力学计算软件thermo-calc(ttni8数据库)软件获得；σ通过如下关系式获得：σ＝94.603-0.0368×t，t为时效温度；气体常数r等于8.314j/(mol·k)，ci为常数；根据公式d^*i＝rtmi(式7)，d^*i＝d^*0,iexp(-q^*i/rt)(式8)；其中，d^*i为时效温度的互扩散系数，mi为原子移动性系数，当t＝1453k和1553k时，结合式7-8，得出q^*i和d^*0,i；然后结合式3，得到有效指数前因子值d0,eff；根据式4，算出粗化激活能qeff；由式5-6，得到时效温度的粗化速率常数。图5为当前方法预测的粗化激活能(实线和虚线)与实验值(散点)的对比(其中，图5中的实验值相应数据来源于下述编号为18-25的文献)，可以看到预测的粗化激活能与实验值具有较好的一致性，误差在10kj/mol以内。图6(a)为当前方法预测的粗化速率常数(实线和虚线，虚线为模拟可接受的误差范围)与实验值(散点)的对比，可以看到预测的粗化速率常数与实验值具有较好的一致性，误差在一个数量级以内。图6(b)为jmatpro软件计算的粗化速率常数(实线和虚线，虚线为模拟可接受的误差范围)与实验值(散点)的对比结果(其中，图6(a)、(b)的实验值数据均来源于下述文献中编号为23、25-32的文献)。由图6(a)和(b)可知，当前方法和jmatpro软件预测的均方误差分别为4.96×10^-50和1.81×10^-48，可以看到当前方法预测的均方误差更小，因此，当前方法相比jmatpro软件预测γ’相演化具有更高的可靠性。

其中，图5和图6的与本申请相应的实验数据引用以下文献：

18、mackayra,nathalmv.γ′coarseninginhighvolumefractionnickel-basealloys[j].actametallurgicaetmaterialia,1990,38(6):993–1005.

19、sadiqs,westd.thecoarseningofγ′particlesinni-al-mo-taandni-al-mo-walloys[j].scriptametallurgica,elsevier,1985,19(7):833–837.

20、daviesc,nashp,stevensr.precipitationinni-co-alalloys[j].journalofmaterialsscience,springer,1980,15(6):1521–1532.

21、kimh,chuns,yaox,etal.gammaprime(γ′)precipitatingandageingbehavioursintwonewlydevelopednickel-basesuperalloys[j].journalofmaterialsscience,springer,1997,32(18):4917–4923./22、gesam,fornaroo,palacioha.coarseningbehaviourofani-basesuperalloyunderdifferentheattreatmentconditions[j].materialsscienceandengineering:a,2007,458(1–2):96–100.

23、vandermolene,oblakj,kriegeo.controlofγ′particlesizeandvolumefractioninthehightemperaturesuperalloyudimet700[j].metallurgicaltransactions,springer,1971,2(6):1627–1633.

24、stevensra,flewittpej.theeffectsofγ′precipitatecoarseningduringisothermalagingandcreepofthenickel-basesuperalloyin-738[j].materialsscienceandengineering,1979,37(3):237–247.

25、footnerp,richardsb.long—termgrowthofsuperalloyγ′particles[j].journalofmaterialsscience,springer,1982,17(7):2141–2153.

26、harat,kobayashis,uenot,etal.estimationofγ/γ′interfacialenergyinni-cobasesuperalloytmw-4m3[j].journalofcrystalgrowth,2019,506:91–96.

27、wangwz,jint,liujl,etal.roleofreandcoonmicrostructuresandγ′coarseninginsinglecrystalsuperalloys[j].materialsscienceandengineering:a,2008,479(1–2):148–156.

28、lih,zuol,songx,etal.coarseningbehaviorofγ′particlesinanickel-basesuperalloy[j].raremetals,2009,28(2):197–201.

29、gesam,fornaroo,palacioha.crecimientodeparticulasγ’enunasuperaleacióncmsx-2[j].matéria(riodejaneiro),2006,11(1):01–07.

30、moshtaghinrs,asgaris.growthkineticsofγ′precipitatesinsuperalloyin-738lcduringlongtermaging[j].materials&design,2003,24(5):325–330.

31、wangh,liud,shiy,etal.matrix-diffusion-controlledcoarseningoftheγ′phaseinwaspaloy[j].metalsandmaterialsinternational,2019,25(6):1410–1419.

32、zhout,dingh,max,etal.microstructureandstress-rupturelifeofhighw-contentcastni-basedsuperalloyafter1000–1100℃thermalexposures[j].materialsscienceandengineering:a,2018,725:299–308.

以上所述实施例的各技术特征可以进行任意的组合，为使描述简洁，未对上述实施例中的各个技术特征所有可能的组合都进行描述，然而，只要这些技术特征的组合不存在矛盾，都应当认为是本说明书记载的范围。

以上所述实施例仅表达了本发明的几种实施方式，其描述较为具体和详细，但并不能因此而理解为对发明专利范围的限制。应当指出的是，对于本领域的普通技术人员来说，在不脱离本发明构思的前提下，还可以做出若干变形和改进，这些都属于本发明的保护范围。因此，本发明专利的保护范围应以所附权利要求为准。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除