基于临床表型和逻辑回归分析的食管鳞癌风险预测方法与流程

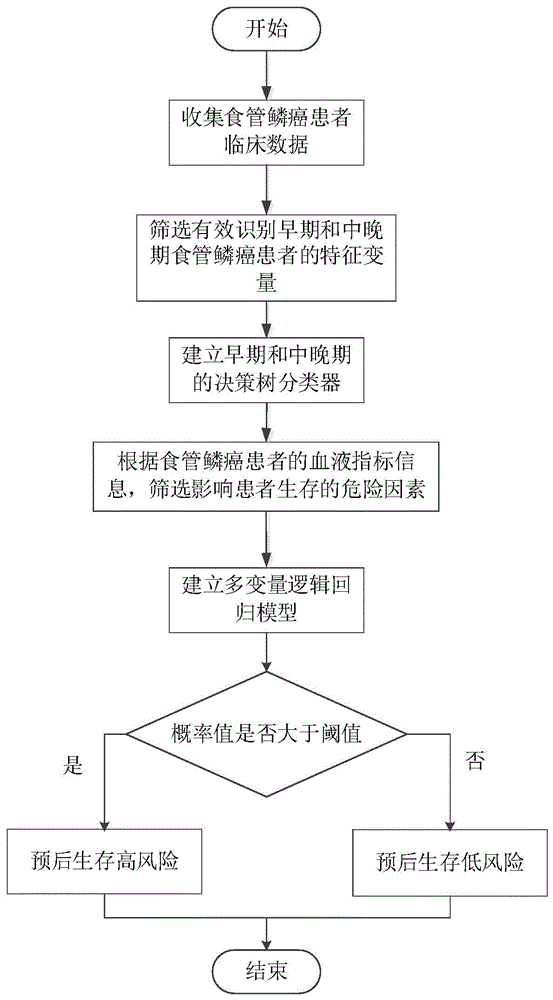
本发明涉及机器学习的
技术领域：
，特别是指一种基于临床表型和逻辑回归分析的食管鳞癌风险预测方法。
背景技术：
：随着癌症发病率逐渐提高，基于模型预测癌症的预后已经广泛应用于不同的疾病，而对癌症患者进行精准的预后仍然是当前所面临的首要问题。临床上检测到的数据是典型的多重共线性、维度高、多噪声的特点，这使得数据本身存在信息冗余、非线性等问题，特别是“高维度”数据特点一直是影响数据挖掘的重大难题，一方面“高维度”使得对数据的处理需要高昂的运算代价，另一方面数据本身也无法直接体现本质属性。近年来，国内外的研究学者针对维度灾难这一问题进行了思考和探讨，并且致力于生物信息的特征提取方法的研究。特征选择和模型构建是学术界和医学领域的一个研究热点和重点，好的特征选择能够提升模型的性能，更能帮助理解数据的特点、底层结构，有助于改善模型。现有技术中，有以下几种方法用于训练数据的特征选择和模型构建：(1)单因素方差分析能够对每一个特征进行测试，衡量该特征和因变量之间的关系，舍弃掉不理想的特征信息；(2)使用皮尔森相关系数衡量变量之间的线性相关性，建立变量之间的关联性；(3)线性回归是常用的一种建模方法。上述方法都是采用常规的方法筛选特征变量进而建立预测模型，使得现有模型的识别率较低，然而，当今的医学界需要一种能准确判断预后风险的方法。技术实现要素：针对上述
背景技术：
中存在的不足，本发明提出了一种基于临床表型和逻辑回归分析的食管鳞癌风险预测方法，解决了现有预测模型由于特征筛选不全，造成识别率低的技术问题。本发明的技术方案是这样实现的：一种基于临床表型和逻辑回归分析的食管鳞癌风险预测方法，其步骤如下：步骤一：获取食管鳞癌患者的临床检测数据，根据临床检测数据筛选出与食管鳞癌患者分类相关性高的特征指标；步骤二：根据与食管鳞癌患者分类相关性高的特征指标构建决策树分类器；步骤三：将待分类的食管鳞癌患者的特征指标输入决策树分类器，得到食管鳞癌患者的分类结果；步骤四：获取食管鳞癌患者术前一周的血液指标信息，通过构建血液指标信息的roc曲线筛选出与食管鳞癌患者生存风险相关性高的血液指标；步骤五：根据与食管鳞癌患者生存风险相关性高的血液指标构建逻辑回归模型；步骤六：将步骤三中分类后的食管鳞癌患者的血液指标输入逻辑回归模型中，得到食管鳞癌患者的预后生存风险概率值；步骤七：判断预后生存风险概率值是否大于阈值γ，若是，预后生存风险为高风险，否则，预后生存风险为低风险，其中，阈值γ表示由roc曲线构造的高风险和低风险的临界值。所述食管鳞癌患者的临床检测数据中的指标包括性别、病理诊断、肿瘤部位、肿瘤的长度、肿瘤的宽度、肿瘤的厚度、肿瘤的类型、病理分化程度、肿瘤浸润程度、阴性、淋巴结阳性转移、t分期、n分期、m分期、第八版tnm分期。所述根据临床检测数据筛选出与食管鳞癌患者分类相关性高的特征指标的方法为：s11、计算临床检测数据中所有指标的卡方值，将卡方值与卡方表一一对应，得到所有指标的p值，筛选出p<0.05的指标作为初步特征指标；其中，初步特征指标具体指性别、病理分化程度、肿瘤浸润程度和淋巴结阳性转移；s12、分别计算每个初步特征指标在属性划分前的信息熵和属性划分后的信息熵，并根据属性划分前的信息熵和属性划分后的信息熵计算初步特征指标的信息增益；s13、根据信息增益的大小对初步特征指标进行筛选，得到与食管鳞癌患者分类相关性高的特征指标；其中与食管鳞癌患者分类相关性高的特征指标包括肿瘤浸润程度和淋巴结阳性转移。所述临床检测数据中所有指标的卡方值的计算方法为：其中，k表示指标类别，指标k取值范围是k∈{1,2,...,nk}，nk表示指标总数，表示指标k的卡方值，i表示指标的属性类别，i∈{1,2,...,mk}，mk表示指标k的属性类别总数，j表示食管鳞癌患者的分类类别，j∈{1,2}，akij表示指标类别为k属性值为i且属于第j类食管鳞癌患者的实际人数，tkij表示指标类别为k属性值为i且属于第j类食管鳞癌患者的理论人数。所述指标类别为k属性值为i且属于第j类食管鳞癌患者的理论人数tkij的计算公式为：所述属性划分前的信息熵的计算方法为：其中，infobefore(h(x))表示不考虑指标类别时患者确诊为食管鳞癌事件x的信息熵，h(x)表示患者确诊为食管鳞癌事件x发生的信息熵，p(xj)表示患者属于第j类食管鳞癌事件发生的概率，j表示食管鳞癌患者的分类类别，j∈{1,2}；所述属性划分后的信息熵的计算方法为：其中，infoafter(h(xk))表示考虑指标类别时患者确诊为食管鳞癌事件xk的信息熵，k表示指标类别，指标k取值范围是k∈{1,2,...,nk}，nk表示指标总数，h(xk)表示患者确诊为食管鳞癌事件xk发生的信息熵，xki表示在指标k属性值为i的患者确诊食管鳞癌事件，p(xki)表示事件xki发生的概率，xkij表示在指标k属性值为i且属于第j类患者确诊食管鳞癌事件，i表示当前指标的属性类别，i∈{1,2,...,mi}，mi表示当前指标的属性类别总数；所述初步特征指标的信息增益的计算方法为：△h(xk)＝infobefore(h(xk))-infoafter(h(xk))，其中，△h(xk)表示初步特征指标k的信息增益，infobefore(h(xk))＝infobefore(h(x))表示不考虑指标类别时事件xk发生的信息熵。所述决策树分类器的构建方法为：将淋巴结阳性转移作为决策树的根节点，将肿瘤浸润程度作为决策树的叶节点构建决策树分类器。所述血液指标信息包括白细胞计数、淋巴细胞计数、单核细胞计数、中性粒细胞计数、嗜酸性粒细胞计数、嗜碱性粒细胞计数、红细胞计数、血红蛋白浓度、血小板计数、总蛋白、白蛋白、球蛋白、凝血酶原时间、活化部分凝血活酶时间、凝血酶时间和纤维蛋白原。所述通过构建血液指标信息的roc曲线筛选出与食管鳞癌患者生存风险相关性高的血液指标的方法为：分别绘制血液指标信息中所有血液指标的roc曲线，根据roc曲线得到每个血液指标的auc和p'值；根据统计学理论，roc曲线下的面积值在1.0和0.5之间，筛选出auc>0.5且p'<0.05的血液指标作为与食管鳞癌患者生存风险相关性高的血液指标；其中，与食管鳞癌患者生存风险相关性高的血液指标包括变量白细胞计数、单核细胞计数、中性粒细胞计数、嗜酸性粒细胞计数和总蛋白。所述逻辑回归模型为：logit(p)＝β0+β1x1+β2x2+…+βmxm，其中，p表示食管鳞癌患者被划分为低风险的概率，logit(p)表示食管鳞癌患者被划分为低风险的概率的对数发生比，x1表示第1个变量的取值，x2表示第2个变量的取值，xm表示第m个变量的取值，m表示逻辑回归模型中变量因子的个数，β0表示逻辑回归模型的常数项，β1表示逻辑回归模型中变量x1对应的系数，β2表示逻辑回归模型中变量x2对应的系数，βm表示逻辑回归模型中变量xm对应的系数。本技术方案能产生的有益效果：(1)本发明利用卡方值和信息熵以及信息增益对临床文本型数据进行筛选特征变量，能够有效识别出早期和中晚期食管鳞癌的特征变量。(2)本发明对早期和中晚期食管鳞癌患者做生存概率曲线分析，分析两组患者的预后生存差异；又根据食管鳞癌患者术前一周的血液检测数据，构建多变量的预测模型；利用多变量的预测模型进行食管鳞癌患者预后风险判断，可以较为精确地判断食管鳞癌患者术后的生存状态，提高风险预测的性能，降低风险预测的成本。附图说明为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。图1是本发明的总体流程图；图2是本发明实施例提供的决策图；图3是本发明实施例提供的生存曲线分析图；图4是本发明实施例提供的白细胞计数roc曲线分析图；图5是本发明实施例提供的单核细胞计数roc曲线分析图；图6是本发明实施例提供的中性粒细胞计数roc曲线分析图；图7是本发明实施例提供的嗜酸性粒细胞计数roc曲线分析图；图8是本发明实施例提供的总蛋白roc曲线分析图；图9是本发明实施例提供的多变量概率预测模型的roc曲线分析图；图10是本发明实施例提供的pni模型的roc曲线分析图；图11是本发明实施例提供的不同模型的风险评估图。具体实施方式下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有付出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。如图1所示，本发明实施例提供了一种基于临床表型和逻辑回归分析的食管鳞癌风险预测方法，具体步骤如下：步骤一：获取食管鳞癌患者的临床检测数据，根据临床检测数据筛选出与食管鳞癌患者分类相关性高的特征指标；所述食管鳞癌患者的临床检测数据中的指标包括性别、病理诊断、肿瘤部位、肿瘤的长度、肿瘤的宽度、肿瘤的厚度、肿瘤的类型、病理分化程度、肿瘤浸润程度、阴性、淋巴结阳性转移、t分期、n分期、m分期、第八版tnm分期。本发明实施例共纳入418例食管鳞癌患者的数据，其中，男性260例(62.2％)，女性158例(37.8％)；肿瘤部位发生在胸上段的有79例(18.9％)，肿瘤部位发生在胸中段的有279例(66.7％)，肿瘤部位发生在胸下段的有60例(14.4％)，同时表明肿瘤大多发生在胸中段；肿瘤病理分化程度中高分化的有26例(6.2％)，肿瘤病理分化程度中中分化的有224例(53.6％)，肿瘤病理分化程度中低分化的有168例(40.2％)；大部分人(62.0％)的肿瘤浸润程度在纤维膜，111例(26.6％)的肿瘤浸润程度在肌层，少部分人的肿瘤浸润程度在粘膜层和粘膜下层；淋巴结阳性转移情况接近50％。所述根据临床检测数据筛选出与食管鳞癌患者分类相关性高的特征指标的方法为：s11、计算临床检测数据中所有指标的卡方值，将卡方值与卡方表一一对应，得到所有指标的p值，筛选出p<0.05的指标作为初步特征指标；所述临床检测数据中所有指标的卡方值的计算方法为：其中，k表示指标类别，指标k取值范围是k∈{1,2,...,nk}，nk表示指标总数，表示指标k的卡方值，i表示指标的属性类别，i∈{1,2,...,mk}，mk表示指标k的属性类别总数，j表示食管鳞癌患者的分类类别，j∈{1,2}，akij表示指标类别为k属性值为i且属于第j类食管鳞癌患者的实际人数，表示指标类别为k属性值为i且属于第j类食管鳞癌患者的理论人数。将上述所有指标的卡方值代入表1，通过查表可以得到当前指标的概率p值，如果p值小于0.05，则该指标被筛选为初步特征指标。表1卡方分布表其中，v表示自由度，自由度的计算公式为：自由度v＝(行数-1)×(列数-1)。以临床检测指标性别为例，分析了性别对食管鳞癌分类的影响。实际统计的男性/女性中患食管鳞癌的分布情况如表2：表2实际统计的男性/女性中患食管鳞癌分布表早期食管鳞癌中晚期食管鳞癌合计确诊患者中患早期食管鳞癌的概率男性a111＝57a112＝20326021.9％女性a121＝58a122＝10015836.7％合计11530341827.5％其中，a111表示实际统计的男性且判定为早期食管鳞癌的人数为57，a112表示实际统计的男性且判定为中晚期食管鳞癌的人数为203，a121表示实际统计的女性且判定为早期食管鳞癌的人数为58，a122表示实际统计的女性且判定为中晚期食管鳞癌的人数为100。男性确诊食管鳞癌患者、女性确诊食管鳞癌患者中属于早期食管鳞癌的占比分别为21.9％、36.7％，两者的差别可能是抽样误差导致，也可能是性别对确诊患者中患早期食管鳞癌真的有影响。首先作出假设，假设性别对食管鳞癌的分类没有影响，即性别与是否患早期食管鳞癌无关。所以，确诊患者中早期食管鳞癌患者的占比实际上为(57+58)/(57+58+203+100)＝27.5％。然后，可以得到如表3所示的理论值。表3男性/女性中患食管鳞癌的理论分布表早期食管鳞癌中晚期食管鳞癌合计男性t111＝72t112＝188260女性t121＝43t122＝115158合计115303418其中，t111表示理论计算得到的男性且判定为早期食管鳞癌的人数为72，t112表示理论计算得到的男性且判定为中晚期食管鳞癌的人数为188，t121表示理论计算得到的女性且判定为早期食管鳞癌的人数为43，t122表示理论计算得到的女性且判定为中晚期食管鳞癌的人数为115。如果性别对食管鳞癌的分类没有影响，计算得到的卡方值会非常小。genuine卡方计算公式得：下一步则根据卡方分布表获取概率p值，然后判断是否有差异。查询卡方分布就需要知道自由度，根据表1可以得到自由度为1，卡方值为11.5时对应的p值小于0.05，则拒绝性别对确认患者中患早期食管鳞癌没有影响这个假设，即性别对确认患者中患早期食管鳞癌有影响。卡方检验分析结果如表2所示，性别(p＝0.001)、病理分化程度(p＝0.000)、肿瘤浸润程度(p＝0.000)和淋巴结阳性转移(p＝0.000)与早期和中晚期食管鳞癌患者具有显著相关性；肿瘤部位(p＝0.227)与食管鳞癌患者没有显著相关性。因此，初步特征指标具体指性别、病理分化程度、肿瘤浸润程度和淋巴结阳性转移；s12、分别计算每个初步特征指标在属性划分前的信息熵和属性划分后的信息熵，并根据属性划分前的信息熵和属性划分后的信息熵计算初步特征指标的信息增益；信息熵用来作为一个系统的信息含量的量化指标。熵主要目的是用来度量不确定性。在机器学习分类问题中，熵越大说明这个类别的不确定性越大，反之越小。所述属性划分前的信息熵的计算方法为：其中，infobefore(h(x))表示不考虑指标类别时患者确诊为食管鳞癌事件x的信息熵，h(x)表示患者确诊为食管鳞癌事件x发生的信息熵，p(xj)表示患者属于第j类食管鳞癌事件发生的概率，j表示食管鳞癌患者的分类类别，j∈{1,2}。所述属性划分后的信息熵的计算方法为：其中，infoafter(h(xk))表示考虑指标类别时患者确诊为食管鳞癌事件xk的信息熵，k表示指标类别，指标k取值范围是k∈{1,2,...,nk}，nk表示指标总数，h(xk)表示患者确诊为食管鳞癌事件xk发生的信息熵，xki表示在指标k属性值为i的患者确诊食管鳞癌事件，p(xki)表示事件xki发生的概率，xkij表示在指标k属性值为i且属于第j类患者确诊食管鳞癌事件，i表示当前指标的属性类别，i∈{1,2,...,mi}，mi表示当前指标的属性类别总数。根据统计上的概率计算公式，可以得到所有做样本中早期食管鳞癌患者所占比例为p1＝115/418＝0.275，中晚期食管鳞癌患者所占比例为p2＝303/418＝0.725，进而可以计算食管鳞癌事件发生的信息熵：h＝-p1log2(p1)-p2log2(p2)＝-0.275log2(0.275)-0.725log2(0.725)≈0.8487对数底数为2是因为只需要信息量满足低概率事件对应于高的信息量，对数的选择是任意的。本发明只是遵循信息论的普遍传统，取2作为对数的底。这样当前数据的信息量(原始状态)用熵计算的结果是0.8487。s13、特征指标的信息增益值越大表明该指标与食管鳞癌患者分类相关性越大，根据信息增益的大小对初步特征指标进行筛选，得到与食管鳞癌患者分类相关性高的特征指标；其中，特征指标包括肿瘤浸润程度和淋巴结阳性转移。信息增益是决策树算法中用来选择特征的指标，信息增益越大，则这个特征的选择性越好。所述初步特征指标的信息增益的计算方法为：△h(xk)＝infobefore(h(xk))-infoafter(h(xk))，其中，△h(xk)表示初步特征指标k的信息增益，infobefore(h(xk))＝infobefore(h(x))表示不考虑指标类别时事件xk发生的信息熵。基于信息熵计算的基础，使用性别这一属性划分早期和中晚期食管鳞癌患者数据，在划分后可以看到数据被划分为两份(男性和女性)，则各分支的信息熵计算如下：因此，依据性别划分后的信息熵为：最后，以性别这一属性为依据进行划分的信息增益为：△h(性别)＝infobefore(h(性别))-infoafter(h(性别))＝0.8487-0.8304＝0.0183选择肿瘤部位这一属性划分早期和中晚期食管鳞癌数据时，在划分后可以看到数据被划分为三部分：胸上段、胸中段和胸下段，则各分支的信息熵计算如下：因此，依据肿瘤部位划分后的信息熵为：最后以肿瘤部位为依据进行划分的信息增益为：△h(肿瘤部位)＝infobefore(h(肿瘤部位))-infoafter(h(肿瘤部位))＝0.8487-0.8438＝0.0049选择肿瘤分化程度这一属性划分早期和中晚期食管鳞癌数据时，在划分后可以看到数据被划分为三部分：高分化、中分化和低分化，则各分支的信息熵计算如下：因此，依据肿瘤分化程度划分后的信息熵为：最后，以肿瘤分化程度这一属性为依据进行划分的信息增益为：△h(肿瘤分化程度)＝infobefore(h(肿瘤分化程度))-infoafter(h(肿瘤分化程度))＝0.8487-0.7967＝0.0520选择肿瘤浸润程度这一属性划分早期和中晚期食管鳞癌数据时，在划分后可以看到数据被划分为四部分：粘膜层、粘膜下层、肌层和纤维膜，则各分支的信息熵计算如下：因此，依据肿瘤浸润程度划分后的信息熵为：最后，以肿瘤浸润程度这一属性为依据进行划分的信息增益为：△h(肿瘤浸润程度)＝infobefore(h(肿瘤浸润程度))-infoafter(h(肿瘤浸润程度))＝0.8487-0.6036＝0.2451使用淋巴结阳性转移这一属性划分早期和中晚期食管鳞癌患者数据，在划分后可以看到数据被划分为两份(未转移和转移)，则各分支的信息熵计算如下：因此，依据淋巴结是否转移划分后的信息熵为：最后，以淋巴结是否转移这一属性为依据进行划分的信息增益为：△h(淋巴结阳性转移)＝infobefore(h(淋巴结阳性转移))-infoafter(h(淋巴结阳性转移))＝0.8487-0.5099＝0.3388各个属性用于早期和中晚期食管鳞癌分类的信息熵以及信息增益值如表4所示。表4早期和中晚期食管鳞癌患者单因素分析表其中，表4的p值是由单因素方差分析得到的。根据各个指标的卡方分析结果，性别(p＝0.001)、病理分化程度(p＝0.000)、肿瘤浸润程度(p＝0.000)和淋巴结阳性转移(p＝0.000)与早期和中晚期食管鳞癌患者的危险因素；再结合信息熵和信息增益值的分析结果，浸润程度(△h＝0.2451)和淋巴结阳性转移(△h＝0.3388)这两个危险因素的信息增益值比较大，将这两个因素用于决策树的根节点信息。步骤二：根据与食管鳞癌患者分类相关性高的特征指标构建决策树分类器；所述决策树分类器的构建方法为：将淋巴结阳性转移作为决策树的根节点，将肿瘤浸润程度作为决策树的叶节点构建决策树分类器。将信息增益最大的属性即淋巴结阳性转移作为第一根节点，肿瘤浸润程度作为第二个节点构建决策树分类器，决策树模型如图2所示。将所收集到的数据带入验证该决策树分类模型，统计各个根节点下的概率分布情况，得到该模型用于早期和中晚期食管鳞癌患者分类的精确度为95.2％。步骤三：将待分类的食管鳞癌患者的特征指标输入决策树分类器，得到食管鳞癌患者的分类结果。食管鳞癌患者的生存率计算：s(t)＝s(t-1)s(t|t-1)其中，生存率又称生存概率或生存函数，它表示一个病人的生存时间长于时间t的概率，用s(t)表示，即s(t)表示t年的生存率，s(t|t-1)表示生存了t-1年又生存t年的条件概率。以时间t为横坐标，s(t)为纵坐标所绘制的曲线称为生存率曲线，它是一条下降的曲线，下降的坡度越陡，表示生存率越低或生存时间越短，其斜率表示死亡速率。如图3所示，不同组间kaplan-meier分析显示，早期组与中晚期组食管鳞癌患者存在显著性差异，中晚期食管鳞癌患者预后生存时间显著少于早期食管鳞癌患者。中晚期食管鳞癌患者的生存时间明显低于早期食管鳞癌患者(对数秩检验，χ2＝19.580，p＝0.000)。根据随访资料分析，早期组3年生存率大于70％，而中晚期组3年生存率为54.03％；早期组6年生存率为49.95％，中晚期组6年生存率为27.07％；早期组11年生存率为37.41％，而中晚期组11年生存率仅为15.45％。步骤四：获取食管鳞癌患者术前一周的血液指标信息，通过构建血液指标信息的roc曲线筛选出与食管鳞癌患者生存风险相关性高的血液指标；所述血液指标信息包括白细胞计数(109/l)、淋巴细胞计数(109/l)、单核细胞计数(109/l)、中性粒细胞计数(109/l)、嗜酸性粒细胞计数(109/l)、嗜碱性粒细胞计数(109/l)、红细胞计数(109/l)、血红蛋白浓度(g/l)、血小板计数(109/l)、总蛋白(g/l)、白蛋白(g/l)、球蛋白(g/l)、凝血酶原时间(s)、活化部分凝血活酶时间(s)、凝血酶时间(s)和纤维蛋白原(mg/dl)。所述通过构建血液指标信息的roc曲线筛选出与食管鳞癌患者生存风险相关性高的血液指标的方法为：分别绘制血液指标信息中所有血液指标的roc曲线，根据roc曲线得到每个血液指标的auc和p'值；根据统计学理论，roc曲线下的面积值在1.0和0.5之间，在auc>0.5且p'<0.05的情况下，说明分类效果越好。筛选出auc>0.5且p'<0.05的血液指标作为与食管鳞癌患者生存风险相关性高的血液指标；其中，与食管鳞癌患者生存风险相关性高的血液指标包括变量白细胞计数、单核细胞计数、中性粒细胞计数、嗜酸性粒细胞计数和总蛋白。受试者工作特征曲线(receiveroperatingcharacteristiccurve，简称roc曲线)是一种坐标图式的分析工具，用于选择最佳的单变量分类模型，在同一模型中设定最佳阈值，auc(areaunderthecurve)表示曲线下面积。对以上16个血液指标进行roc曲线分析，分析结果如下：白细胞计数(109/l)(auc＝0.663，p＝0.007)、淋巴细胞计数(109/l)(auc＝0.508，p＝0.893)、单核细胞计数(109/l)(auc＝0.669，p＝0.005)、中性粒细胞计数(109/l)(auc＝0.650，p＝0.010)、嗜酸性粒细胞计数(109/l)(auc＝0.647，p＝0.015)、嗜碱性粒细胞计数(109/l)(auc＝0.555，p＝0.362)、红细胞计数(109/l)(auc＝0.455，p＝0.454)、血红蛋白浓度(g/l)(auc＝0.427，p＝0.227)、血小板计数(109/l)(auc＝0.584，p＝0.162)、总蛋白(g/l)(auc＝0.622，p＝0.043)、白蛋白(g/l)(auc＝0.605，p＝0.082)、球蛋白(g/l)(auc＝0.537，p＝0.539)、凝血酶原时间(s)(auc＝0.443，p＝0.346)、活化部分凝血活酶时间(s)(auc＝0.609，p＝0.072)、凝血酶时间(s)(auc＝0.407，p＝0.125)、纤维蛋白原(mg/dl)(auc＝0.597，p＝0.107)，具体结果如表5所示。表5单变量roc曲线分析其中，表5中的p值是由roc曲线分析得到的。根据对16个血液指标的受试者工作特征曲线分析，筛选出对预后生存风险影响大的危险因素。roc曲线通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和特异性，再以敏感性为纵坐标，(1-特异性)为横坐标绘制成曲线，曲线下面积越大，分类准确性越高；在受试者工作特征曲线上，最靠近坐标图左上方的点为敏感性和特异度都较高的临界值，即单个指标的最佳分类阈值，该阈值的选择通过约登指数来判定，其中约登指数的计算表达式为：约登指数＝灵敏度+特异性-1。通过roc曲线分析，找到了五个重要的特征变量：白细胞计数、单核细胞计数、中性粒细胞计数、嗜酸性粒细胞计数和总蛋白。具体分析结果如下：图4为白细胞计数(109/l)(auc＝0.663，95％ci:[0.549,0.778]，p＝0.007)的roc曲线分析图，灵敏度为71.9％，特异度为63.9％，约登指数＝灵敏度+特异性-1＝0.605+0.719-1＝0.358，白细胞计数的最佳阈值为6.05，将白细胞计数分为两组(高白细胞计数组：>6.05×109/l，低白细胞计数组：≤6.05×109/l)；图5为单核细胞计数(109/l)(auc＝0.669，95％ci:[0.561,0.776]，p＝0.005)的roc曲线分析图，灵敏度为78.1％，特异度为43.4％，约登指数＝灵敏度+特异性-1＝0.781+0.434-1＝0.215，单核细胞计数的最佳阈值为0.35，将单核细胞计数分为两组(高单核细胞计数组：>0.35×109/l，低单核细胞计数组：≤0.35×109/l)；图6为中性粒细胞计数(109/l)(auc＝0.650，95％ci:[0.537,0.764]，p＝0.010)的roc曲线图，灵敏度为78.1％，特异度为55.4％，约登指数＝灵敏度+特异性-1＝0.781+0.554-1＝0.335，中性粒细胞计数的最佳阈值为3.35，将中性粒细胞计数分为两组(高中性粒细胞计数组：>3.35×109/l，低中性粒细胞计数组：≤3.35×109/l)；图7为嗜酸性粒细胞计数(109/l)(auc＝0.647，95％ci:[0.538,0.756]，p＝0.015)的roc曲线图，灵敏度为84.4％，特异度为42.4％，约登指数＝灵敏度+特异性-1＝0.844+0.424-1＝0.226，嗜酸粒细胞计数的最佳阈值为0.05，将嗜酸性粒细胞计数分为两组(高嗜酸粒细胞计数组：>0.05×109/l，低嗜酸粒细胞计数组：≤0.05×109/l)；图8为总蛋白(g/l)(auc＝0.622，95％ci:[0.515,0.729]，p＝0.043)的roc曲线图，灵敏度为90.6％，特异度为32.5％，约登指数＝灵敏度+特异性-1＝0.906+0.325-1＝0.231，总蛋白的最佳阈值为67.5，将总蛋白分为两组(高总蛋白组：>67.5g/l，低总蛋白组：≤67.5g/l)。高指标组、低指标组为定性划分，高指标组记为“1”，低指标组记为“0”。步骤五：根据roc曲线筛选出的与食管鳞癌患者生存风险相关性高的血液指标构建逻辑回归模型；所述逻辑回归模型为：logit(p)＝β0+β1x1+β2x2+…+βmxm，其中，p表示食管鳞癌患者被划分为低风险的概率，logit(p)表示食管鳞癌患者被划分为低风险的概率的对数发生比，x1表示第1个变量的取值，x2表示第2个变量的取值，xm表示第m个变量的取值，m表示逻辑回归模型中变量因子的个数，β0表示逻辑回归模型的常数项，β1表示逻辑回归模型中变量x1对应的系数，β2表示逻辑回归模型中变量x2对应的系数，βm表示逻辑回归模型中变量xm对应的系数。步骤六：将步骤三中分类后的食管鳞癌患者的血液指标输入逻辑回归模型中，得到食管鳞癌患者的预后生存风险概率值；步骤七：判断预后生存风险概率值是否大于阈值γ，若是，预后生存风险为高风险，否则，预后生存风险为低风险。其中，阈值γ表示由roc曲线构造的高风险和低风险的临界值。根据对血液因素的单因素分析，选择白细胞计数、单核细胞计数、中性粒细胞计数、嗜酸性粒细胞计数和总蛋白这五个指标作为特征变量进行预测建模。将数据分为测试集和验证集，通过对测试集进行分析建模，然后用验证集数据验证该模型的有效性和可靠性。将五个预测变量白细胞计数、单核细胞计数、中性粒细胞计数、嗜酸性粒细胞计数和总蛋白在测试集中纳入多变量回归分析，分析结果如表6所示。表6多变量逻辑回归分析进而，建立的逻辑回归模型如下：logit(p)＝0.241-2.554×白细胞计数-0.453×单核细胞计数+1.012×中性粒细胞计数-2.484×嗜酸性细胞计数-0.527×总蛋白进一步地，可以得到概率估计公式为：其中，p表示食管鳞癌患者被划分为低风险的概率，logit(p)表示食管鳞癌患者被划分为低风险的概率的对数发生比，x1表示白细胞计数的取值，x2表示单核细胞计数的取值，x3表示中性粒细胞的取值，x4表示嗜酸性粒细胞计数的取值，x5表示总蛋白的取值，β0＝0.241表示逻辑回归模型的常数项，β1＝-2.554表示变量x1对应的系数，β2＝-0.453表示变量x2对应的系数，β3＝1.012表示变量x3对应的系数，β4＝-2.484表示变量x4对应的系数，β5＝-0.527表示变量x5对应的系数。得到的多变量概率预测回归模型进行风险预测的roc曲线如图9所示，预测风险的准确率为86.1％，基于多变量概率预测模型不同截断值的预测效果如表7所示。其中，灵敏度为79.7％，特异性为82.6％，约登指数＝灵敏度+特异性-1＝0.797+0.826-1＝0.623，对应的最佳阈值为0.046755，换句话说，当计算得到的概率值小于该阈值则该对象处于预后低风险，反正则属于预后高风险。表7基于多变量概率预测模型不同截断值的预测效果截断值敏感度1-特异性约登指数01100.00396910.9130.0870.0066510.870.130.010840.8550.2610.5940.013730.8260.2610.5650.026270.7970.1740.6230.0467550.710.0870.6230.0570840.6960.0870.6090.0610880.6520.0430.6090.0779590.5650.0430.5220.0943320.5070.0430.4640.0973610.4780.0430.4350.1186220.4490.0430.4060.1427590.420.0430.3770.1518040.4060.0430.3630.1852820.3770.0430.3340.2200020.3620.0430.3190.2746150.3480.0430.3050.3761030.3190.0430.2760.4380910.1590.0430.1160.5035790.130.0430.0870.6169430.0430.04300.7258730.0140.043-0.0291000医学上常用的预后营养指标模型如下：pni＝白蛋白+5×淋巴细胞计数根据该模型在测试集中进行风险预测，结果如图10所示，预测预后风险的准确率为57.9％，其中，灵敏度为61.9％，特异性为63.1％，约登指数＝灵敏度+特异性-1＝0.619+0.631-1＝0.250，对应的最佳阈值为51.75。将该多变量回归模型以及pni模型在验证集进行验证，评价该模型的预测准确率。多变量概率预测回归模型在验证集中进行最终的分类结果验证如表8所示：表8分类矩阵根据该分类矩阵可知，实际是低风险，模型预测也是低风险的数量是10；实际是低风险，模型预测却是高风险的数量是4；实际是高风险，模型预测却是低风险的数量是3；实际是高风险，模型预测也是高风险的数量是6。预测模型评价指标：其中，acc表示分类模型所有判断正确的结果占总观测值的比重；ppv表示在实际为低风险的所有结果中，预测模型是低风险的比重；npv表示在实际为高风险的所有结果中，预测模型是高风险的比重；r表示召回率，是预测和实际都为低风险的样本数量与预测为低风险的样本数量之比；f1-measure表示是ppv和r的加权调和平均值。根据以上计算公式，可以计算该多变量概率预测模型的准确率为acc＝16/23≈69.57％，实际为低风险的所有结果中，预测模型是低风险的比重是ppv＝10/14≈71.43％,实际为高风险的所有结果中，预测模型是高风险的比重是npv＝6/9≈66.67％，预测和实际都为低风险的样本数量与预测为低风险的样本数量之比，即召回率为r＝10/13≈76.92％，ppv和r的加权调和平均值即f1-measure＝2×0.7143×0.7692/(0.7143+0.7692)≈74.07％。同样地，得到pni模型在验证集中进行最终的分类结果验证如表9所示：表9分类矩阵根据该分类矩阵可知，实际是低风险，模型预测也是低风险的数量是5；实际是低风险，模型预测却是高风险的数量是9；实际是高风险，模型预测却是低风险的数量是2；实际是高风险，模型预测也是高风险的数量是7。然后，根据预测模型评价指标计算公式，可以计算该pni预测模型的准确率为acc＝12/23≈52.17％，实际为低风险的所有结果中，预测模型是低风险的比重是ppv＝5/14≈35.71％，实际为高风险的所有结果中，预测模型是高风险的比重是npv＝7/9≈77.78％，预测和实际都为低风险的样本数量与预测为低风险的样本数量之比，即召回率为r＝5/7≈71.43％，ppv和r的加权调和平均值即f1-measure＝2×0.3571×0.7143/(0.3571+0.7143)≈47.62％。最后，通过多变量概率预测模型与pni模型各个评价指标的对比，如图11所示。综合各项风险评估指数，可以看出本发明建立的多变量概率预测模型具有较好的预测能力。以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页1 2 3 

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除