基于综合距离的在线可更新暖通空调传感器故障检测方法与流程

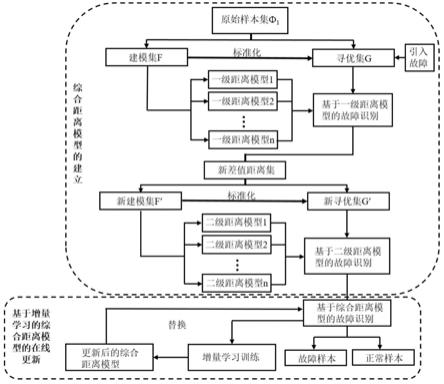
[0001]
本发明涉及暖通空调系统监控及故障诊断技术领域，具体涉及基于综合距离的在线可更新暖通空调传感器故障检测方法。


背景技术：

[0002]
随着现代科技社会的飞速发展，建筑行业不可忽视的成为了全国能源消耗的巨头之一，其中，暖通空调能耗所占建筑业内的住宅建筑和商业建筑近一半的能耗量。而在暖通空调系统中，传感器一旦发生故障将导致暖通空调系统难以保持运行在高效、节能的控制策略中，因此，能否尽早且准确的将发生故障的传感器检测并划分出来对暖通空调系统节能减耗具备重要意义。
[0003]
传统的故障检测模型通常通过样本建立单一的故障检测模型，这种单一检测模型仅对于单一的故障标签和均匀分布的原始样本有着较好的检测性能，对于多故障类别、原始样本分布不均的问题就显得束手无策。主成分分析算法主要通过保留主要信息舍弃部分信息来建立故障检测模型，然而舍弃的这部分信息可能存在着样本的重要信息，容易导致过拟合现象的加剧；单类支持向量机算法是典型的处理二检测问题的检测模型，一旦样本数据缺失或者非线性，检测模型的性能就会显著下降；k均值聚类算法对于数据的要求高，不适用于有噪音和异常点的数据集；自动编码器存在着计算能力弱，容易过拟合缺点，更适用于小样本数据。上述模型也都是离线模型，不存在数据和模型的更新。然而在暖通空调系统中，其存储的建筑空调数据存在着多度量，多维度，地域性、大量且实时更新等特点，单一的检测模型难以在特征空间中充分利用样本数据信息建模，在全局中容易存在错误检测、检测性能不高等问题；而且上述的四个算法对同一个样本集建模的侧重不同，难以同时充分利用空调领域原始样本中的数据信息，也无法针对不同的样本集同时取得最佳的故障检测性能。


技术实现要素：

[0004]
基于以上问题，本发明提供基于综合距离的在线可更新暖通空调传感器故障检测方法。通过构建两层距离模型，在第一层通过四种单一算法建立相应的单一距离模型作为一级距离模型获取距离减边界距离的新差值距离集；在第二层进一步通过新差值距离构建上述四种单一距离模型中检测性能最高的距离模型作为最终的二级距离模型，从而实现对传感器故障的检测。新差值距离由于其去除了边界信息，相比于原始样本变得更加精悍，通过将新差值距离取代原始样本作为输入，来提高故障检测模型对故障检测的正确率并降低错识率，有效的克服了传统的单一距离模型对小幅值故障不敏感的局限性。其中一级距离模型根据实时更新的样本集进行筛选更新，形成动态的综合距离模型，提高了暖通空调系统中传感器的故障检测性能，也解决了传统单一距离模型中在在线更新上的问题。
[0005]
为实现上述技术效果，本发明采用的技术方案是：
[0006]
基于综合距离的在线可更新暖通空调传感器故障检测方法，包括如下步骤：
[0007]
s1、建立综合距离模型，具体流程如下：
[0008]
1)将暖通空调系统内的正常运行数据作为原始样本集；
[0009]
2)将原始样本集分为建模集和寻优集两部分，在寻优集中引入故障；对寻优集进行和建模集相同的标准化处理；
[0010]
3)选取主成分分析算法、单类支持向量机算法、k均值聚类算法和自动编码器算法，输入标准化的建模集训练为四个一级距离模型，通过寻优集对一级距离模型的参数进行寻优，建立最优的四个一级距离模型，剔除检测性能弱的一级距离模型；定义每个一级距离模型的输出距离与其对应的模型边界距离的差值为新差值距离，组合筛选后的最优一级距离模型的输出结果，形成新差值距离集；
[0011]
4)通过标准化后的新差值距离集分为新建模集和新寻优集，建立基于以上四种算法的二级距离模型，选取性能最好的二级距离模型作为最终的二级距离故障检测模型；其中，二级距离模型的输出结果为单个距离，将其和输出单个距离对应的边界距离作比较，小于则为正常样本，储存至正常样本集a1中；大于则为故障样本，储存至故障样本集a2中；
[0012]
s2、样本数据更新后启动增量学习训练更新综合距离模型，具体流程为：数据更新后启动增量学习训练新增样本集ф2，将新增样本集输入到s1中得到的综合距离模型内，输出结果同样被划分为新增正常样本集b1和新增故障样本集b2；将b2和4)中的a1、a2混合形成更新后的样本集，训练出更新后的关于综合距离的故障检测模型。
[0013]
进一步地，主成分分析算法具体故障检测流程为：将原始样本数据x投影到主元空间，分解为主元向量和非主元向量通常认为主元向量包含原始样本数据中的重要信息，而非主元向量则反映数据的各种误差关系，即可定义主成分分析算法的单一距离q
p
为非主元向量的欧式距离的平方：
[0014][0015]
那么，q
p
对应的边界距离表示为：
[0016][0017]
式(2)中，l为模型的主成分个数，c
α
为置信度为α的标准正太分布置信限，λ为标准化后的原始样本矩阵的协方差阵r的特征值；即对应的新差值距离d
p
为：
[0018]
d
p
＝q
p-t
p
ꢀꢀꢀꢀ
(3)
[0019]
当d
p
>0时，样本超出边界距离范围，检测为故障样本，反之则检测为正常样本；
[0020]
所述单类支持向量机算法故障检测流程为：通过训练正常样本，在其特征空间中构造一个最大化距离平面以实现训练样本与原点距离的最大化，即根据样本y，若样本y到原点的距离小于该距离平面则检测为故障样本，定义单类支持向量机算法的单一距离qo为最大化距离平面f(y)的负值，其表达式为：
[0021][0022]
式(4)中，ω和ρ为决策最大化距离平面的参数，ψ为原始样本在特征空间中的映
射，此时q
o
对应的边界距离t
o
＝0，即对应的新差值距离d
o
为：
[0023]
d
o
＝q
o-t
o
＝q
o
(5)
[0024]
即当d
o
>0时，样本检测为故障样本，反之则检测为正常样本；
[0025]
所述k均值聚类算法故障检测流程为：通过以距离相似度进行检测，将原始样本数据分为k类，定义聚类中心为质心o；计算聚类中非质心样本到每个质心的欧氏距离，通过最小化该欧式距离来寻找最终质心的个数，即聚类个数；根据样本z，定义k均值聚类算法的单一距离q
k
为最小化后的欧氏距离h(z,o)，其表达式为：
[0026][0027]
将计算得到的q
k
从小到大排列，选择第95百分位数的欧氏距离作为q
k
对应的边界距离t
k
，即对应的新差值距离d
k
为：
[0028]
d
k
＝q
k-t
k
ꢀꢀꢀꢀ
(7)
[0029]
若得出d
k
>0，则认为样本不属于任何一个聚类，距离模型检测为故障样本；反之检测为正常样本；
[0030]
所述自动编码器算法的故障检测流程为：将原始样本输入到隐含层，进行编码重构解码生成重构样本，通过最小化原始样本和重构样本之间的均方差来检测故障样本；根据m维样本p，定义自动编码器算法的单一距离q
a
为最小化后的均方差mse(p,p
′
)，其表达式为：
[0031][0032]
将计算得到的q
a
从小到大排列，选择第95百分位数的q
a
作为其对应的边界距离t
a
，即对应的新差值距离d
a
为：
[0033]
d
a
＝q
a-t
a
ꢀꢀꢀ
(9)
[0034]
若得出的d
a
>0，则认为重构样本与原始样本不一致，检测为故障样本；反之则检测为正常样本；
[0035]
所述增量学习的综合距离模型更新的故障检测流程为：原始数据集ф1为建模集f和寻优集g的集合：ф1＝{f,g}；基于ф1建立的初始综合距离的故障检测模型可以看作是，通过ф1建立一个距离模型，距离模型对应有一组参数θ，即可得到距离模型和θ的联合概率分布p，当p最大时，意味着此时的θ与基于ф1建立的距离模型最为适配，即：
[0036][0037]
样本更新后得到新增样本集ф2，通过初始综合距离的故障检测模型检测为正常样本集b1和故障样本集b2，将b2和ф1混合，形成更新后的样本集ф1′
，则基于ф1′
建立的更新后的综合距离故障检测模型希望该距离模型预期与建立距离模型对应产生的一组参数θ'的联合概率分布p
′
达到最大：
[0038][0039]
式(10)和式(11)中，n1,n2分别为更新前后的样本数量；p
′
达到最大时，意味着综合距离模型与其对应的一系列参数是最优适配，此时的综合距离模型达到最优，检测结果输出为正常样本集a1′
和故障样本集a2′
。
[0040]
与现有技术相比，本发明的有益效果是：本发明通过构建两层距离模型，通过构建两层距离模型，在第一层通过四种单一算法建立相应的单一距离模型作为一级距离模型获取距离减边界距离的新差值距离集；在第二层进一步通过新差值距离构建上述四种单一距离模型中检测性能最高的距离模型作为最终的二级距离模型，从而实现对传感器故障的检测。新差值距离由于其去除了边界信息，相比于原始样本变得更加精悍，通过将新差值距离取代原始样本作为输入，来提高故障检测模型对故障检测的正确率并降低错识率，有效的克服了传统的单一距离模型对小幅值故障不敏感的局限性。其中一级距离模型根据实时更新的样本集进行筛选更新，形成动态的综合距离模型，提高暖通空调系统中传感器的故障检测性能，也解决了单一距离模型在在线更新上的问题。
附图说明
[0041]
图1为实施例1和2中基于综合距离的在线可更新暖通空调传感器故障检测方法的流程图；
[0042]
图2为实施例1和2中基于增量学习的模型更新原理图；
[0043]
图3为实施例2中在不同故障幅值下的一级距离模型得检测性能比较图；
[0044]
图4为实施例2中基于主成分分析算法的一级距离模型的距离q
p
的分布图；
[0045]
图5为实施例2中基于单类支持向量机算法的一级距离模型的距离q
o
的分布图；
[0046]
图6为实施例2中基于k均值聚类算法的一级距离模型的距离q
k
的分布图；
[0047]
图7为实施例2中基于自动编码器算法的一级距离模型的距离q
a
的分布图；
[0048]
图8为实施例2中在不同故障幅值下的二级距离模型的检测性能比较图；
[0049]
图9为实施例2中二级距离模型的距离q
k
′
的分布图。
具体实施方式
[0050]
为使本发明的目的、技术方案和优点更加清楚明白，下面结合实施例和附图，对本发明作进一步的详细说明，本发明的示意性实施方式及其说明仅用于解释本发明，并不作为对本发明的限定。
[0051]
实施例1：
[0052]
参见图1和图2，基于综合距离的在线可更新暖通空调传感器故障检测方法，包括如下步骤：
[0053]
s1、建立综合距离模型，具体流程如下：
[0054]
1)将暖通空调系统内的正常运行数据作为原始样本集；
[0055]
2)将原始样本集分为建模集和寻优集两部分，在寻优集中引入故障；对寻优集进行和建模集相同的标准化处理；
[0056]
3)选取主成分分析算法、单类支持向量机算法、k均值聚类算法和自动编码器算法，输入标准化的建模集训练为四个一级距离模型，通过寻优集对一级距离模型的参数进行寻优，建立最优的四个一级距离模型，剔除检测性能弱的一级距离模型；定义每个一级距离模型的输出距离与其对应的模型边界距离的差值为新差值距离，组合筛选后的最优一级距离模型的输出结果，形成新差值距离集；
[0057]
4)通过标准化后的新差值距离集分为新建模集和新寻优集，建立基于以上四种算
法的二级距离模型，选取性能最好的二级距离模型作为最终的二级距离故障检测模型；其中，二级距离模型的输出结果为单个距离，将其和输出单个距离对应的边界距离作比较，小于则为正常样本，储存至正常样本集a1中；大于则为故障样本，储存至故障样本集a2中；
[0058]
综合距离模型作为二检测模型，将样本在数据空间中映射为距离，和边界距离进行比较，从而对正常样本和故障样本进行划分；此时输出结果为整个综合距离模型的故障检测结果，是将样本通过模型检测后的正常样本集和故障样本集。
[0059]
s2、样本数据更新后启动增量学习训练更新综合距离模型，具体流程为：数据更新后启动增量学习训练新增样本集ф2，将新增样本集输入到s1中得到的综合距离模型内，输出结果同样被划分为新增正常样本集b1和新增故障样本集b2；将b2和4)中的a1、a2混合形成更新后的样本集，训练出更新后的关于综合距离的故障检测模型。
[0060]
在本实施例中，选取主成分分析，单类支持向量机算法，k均值聚类，自动编码器四个算法，本发明通过构建两层距离模型，通过构建两层距离模型，在第一层通过四种单一算法建立相应的单一距离模型作为一级距离模型获取距离减边界距离的新差值距离集；在第二层进一步通过新差值距离构建上述四种单一距离模型中检测性能最高的距离模型作为最终的二级距离模型，从而实现对传感器故障的检测。新差值距离由于其去除了边界信息，相比于原始样本变得更加精悍，通过将新差值距离取代原始样本作为输入，来提高故障检测模型对故障检测的正确率并降低错识率，有效的克服了传统的单一距离模型对小幅值故障不敏感的局限性。其中一级距离模型根据实时更新的样本集进行筛选更新，形成动态的综合距离模型，提高暖通空调系统中传感器的故障检测性能，也解决了传统单一距离模型中在在线更新上的问题。
[0061]
本实施例中，所述主成分分析算法具体故障检测流程为：将原始样本数据x投影到主元空间，分解为主元向量和非主元向量通常认为主元向量包含原始样本数据中的重要信息，而非主元向量则反映数据的各种误差关系，即可定义主成分分析算法的单一距离q
p
为非主元向量的欧式距离的平方：
[0062][0063]
那么，q
p
对应的边界距离表示为：
[0064][0065]
式(2)中，l为模型的主成分个数，c
α
为置信度为α的标准正太分布置信限，λ为标准化后的原始样本矩阵的协方差阵r的特征值；即对应的新差值距离d
p
为：
[0066]
d
p
＝q
p-t
p
ꢀꢀꢀ
(3)
[0067]
当d
p
>0时，样本超出边界距离范围，检测为故障样本，反之则检测为正常样本；
[0068]
所述单类支持向量机算法故障检测流程为：通过训练正常样本，在其特征空间中构造一个最大化距离平面以实现训练样本与原点距离的最大化，即根据样本y，若样本y到原点的距离小于原点到该距离平面则检测为故障样本，定义单类支持向量机算法的单一距
离qo为最大化距离平面f(y)的负值，其表达式为：
[0069][0070]
式(4)中，ω和ρ为决策最大化距离平面的参数，ψ为原始样本在特征空间中的映射，此时qo对应的边界距离to＝0，即对应的新差值距离do为：
[0071]
d
o
＝q
o-t
o
＝q
o
ꢀꢀ
(5)
[0072]
即当d
o
>0时，样本检测为故障样本，反之则检测为正常样本；
[0073]
所述k均值聚类算法故障检测流程为：通过以距离相似度进行检测，将原始样本数据分为k类，定义聚类中心为质心o；计算聚类中非质心样本到每个质心的欧氏距离，通过最小化该欧式距离来寻找最终质心的个数，即聚类个数；根据样本z，定义k均值聚类算法的单一距离q
k
为最小化后的欧氏距离h(z,o)，其表达式为：
[0074][0075]
将计算得到的q
k
从小到大排列，选择第95百分位数的欧氏距离作为q
k
对应的边界距离t
k
，即对应的新差值距离d
k
为：
[0076]
d
k
＝q
k-t
k
ꢀꢀꢀ
(7)
[0077]
若得出d
k
>0，则认为样本不属于任何一个聚类，距离模型检测为故障样本；反之检测为正常样本；
[0078]
所述自动编码器算法的故障检测流程为：将原始样本输入到隐含层，进行编码重构解码生成重构样本，通过最小化原始样本和重构样本之间的均方差来检测故障样本；根据m维样本p，定义自动编码器算法的单一距离q
a
为最小化后的均方差mse(p,p
′
)，其表达式为：
[0079][0080]
将计算得到的q
a
从小到大排列，选择第95百分位数的q
a
作为其对应的边界距离t
a
，即对应的新差值距离d
a
为：
[0081]
d
a
＝0
a-t
a
ꢀꢀꢀ
(9)
[0082]
若得出的d
a
>0，则认为重构样本与原始样本不一致，检测为故障样本；反之则检测为正常样本；
[0083]
所述增量学习的综合距离模型更新的故障检测流程为：原始数据集ф1为建模集f和寻优集g的集合：ф1＝{f,g}；基于ф1建立的初始综合距离的故障检测模型可以看作是，通过ф1建立一个距离模型，距离模型对应有一组参数θ，即可得到距离模型和θ的联合概率分布p，当p最大时，意味着此时的θ与基于ф1建立的距离模型最为适配，即：
[0084][0085]
样本更新后得到新增样本集ф2，通过初始综合距离的故障检测模型检测为正常样本集b1和故障样本集b2，将b2和ф1混合，形成更新后的样本集ф1′
，则基于ф1′
建立的更新后的综合距离故障检测模型希望该距离模型预期与建立距离模型对应产生的一组参数θ'的联合概率分布p
′
达到最大：
[0086]
[0087]
式(10)和式(11)中，n1,n2分别为更新前后的样本数量；p
′
达到最大时，意味着综合距离模型与其对应的一系列参数是最优适配，此时的综合距离模型达到最优，检测结果输出为正常样本集a1′
和故障样本集a2′
。
[0088]
实施例2：
[0089]
参见图1-9，本实施例以冷冻水侧供水温度的传感器故障为例，实验数据采集于武汉市某高校的复合式地源热泵系统的正常运行状态数据，该地源热泵系统的主机为一台额定制冷量为30.4kw的热泵机组。实验数据的采集时间为该机组7、8两月份，时段为上午8点到下午20点，每隔半个小时记录一次数据，记录的特征参数如表1所示。
[0090]
表1热泵机组特征参数的符号及意义
[0091][0092]
1)确定原始样本集
[0093]
筛选明显的异常数据后的数据共772组，作为原始样本集，按照时间顺序令前412组为建模集，后360组为寻优集，寻优集引入一定的正负小幅值的传感器故障。
[0094]
2)评价指标
[0095]
引入t1来表征故障样本在寻优集中的检测准确率。式(10)中，n1表示寻优集中故障样本的总个数，t
n
表示检测故障样本的准确个数：
[0096][0097]
引入t2来表征寻优集中正常样本的错识率。式(11)中，n2表示寻优集中正常样本的总个数，t
f
表示正常样本中检测错误的个数：
[0098][0099]
引入roc曲线来评价t1和t2的相关性。通过将t2作为横坐标，t1作为纵坐标，建立roc曲线，用来表征距离模型的性能。
[0100]
引入roc曲线下包围的面积值记作auc值，该值可以直接的评价距离模型的性能。auc∈[0.1,1]，显然，auc值越大，其模型检测性能越高；当auc值为0.5及以下时，检测模型的检测效果与随机检测类似，不具备故障检测能力。
[0101]
3)参数选择
[0102]
3.1一级距离模型的参数选择
[0103]
表2一级距离模型的相关参数及对应边界距离
[0104][0105]
3.2二级距离模型的参数选择
[0106]
选取在四种算法中性能最好的算法建立最终的二级距离模型(将一级距离模型中的输出结果分别通过四种算法建立二级距离模型，比较得到检测性能最好的作为本实施例最终的二级距离模型)，其特征参数选择如下：
[0107]
表3二级距离模型的相关参数及对应边界距离
[0108][0109][0110]
本实例在比较之下选取k均值聚类算法建立最终的二级距离模型(选择过程将在4.2中展示)，此时，根据新差值样本集q＝(q1,q2,
…
,q
s
)，随机分为k
′
个聚类，通过最小化每类非质心样本与质心的欧式距离h
′
(z,o)来计算得到二级距离，其表达式为：
[0111][0112]
将计算得到的q
′
k
从小到大排列，选择第95百分位数的欧氏距离作为q
′
k
对应的边界距离t
′
k
，若得出q
′
k
>t
′
k
，则检测为故障样本；反之检测为正常样本；二级距离模型的输出结果即为综合距离模型的最终输出结果，用于后续增量学习的模型更新。表4为二级距离模型在不同参数k
′
值下的错识率，可以看到当k
′
在2及2以上时，错识率已超过10％，故本实施例确定k
′
＝1，来建立最终的二级距离模型。
[0113]
表4二级距离模型中不同k值下的错识率
[0114][0115]
4)检测结果
[0116]
4.1一级距离算法的筛选
[0117]
从图3种可以看到，在负向上的故障幅值中，基于单类支持向量机的一级距离模型取得了最优的检测性能，整体auc值在其他三个一级距离模型之上，基于k均值聚类的一级距离模型取得第二优的检测性能；而在正向上，基于k均值聚类的一级距离模型取得最优。整体上基于k均值聚类的一级距离模型检测性能较好，而基于自动编码器的一级距离模型
的auc曲线位置靠下，取得相对较差的检测性能。在图4到图7中，边界距离之上的样本为检测错误的样本，为了样本分布表达清晰，q
o
和q
a
的纵坐标轴与其余距离空间的范围相比更小。可以看到，q
p
和q
o
的距离空间中的样本分布均匀，容易被边界距离检测出来，而q
o
和q
a
在距离空间中，样本分布较紧凑，边界距离胶着在样本分布中，不容易被边界距离检测；q
a
的距离空间上识别错误的样本相比q
o
太多，故最终剔除自动编码器距离模型，选取的一级距离模型算法为主成分分析，单类支持向量机算法和k均值聚类。
[0118]
4.2二级距离算法的比较选择
[0119]
计算结果绘制auc值变化曲线图。如图8所示，2-主成分分析，2-单类支持向量机算法，2-k均值聚类，2-自动编码器分别表示这四种算法作为二级距离模型下建立的相应模型。
[0120]
可以看出在四种二级距离模型中，k均值聚类距离模型比其他距离模型都要表现的好；auc值均值在0.88及以上。对比可以得出，主成分分析距离模型的性能最低，k均值聚类距离模型性能最优。故选取k均值聚类作为最终的二级距离模型。图9展示了二级距离模型q
k
′
的距离分布图。
[0121]
4.3不同模型的检测性能比较
[0122]
本实施例将用所建立的综合距离模型和多数投票组合距离模型，基于原始样本集建立的主成分分析，单类支持向量机算法，k均值聚类，自动编码器这四种单个距离模型共六种方法作比较。表中故障幅值随机选取。
[0123]
表5不同模型下的在不同故障幅值下的auc值
[0124][0125]
表5可以看出，综合距离模型取得了最优的故障检测性能，auc值均在0.96之上；比基于是原始样本集建立的单一距离模型的最大值提升了4％左右，比多数投票综合策略下也有一定的提高，且在不同故障幅值下的auc值保持一个稳定的高水平。图9也可以直观的看到q
k
′
相比于q
k
在距离空间中样本更加分散，边界距离检测错误的样本更少，可以实现更好的检测结果。
[0126]
表6是所有故障检测方法在未引入故障幅值的寻优集上的错识率，可以看出，综合距离模型的错识率显著降到了0.83％，而其它距离模型则在4％和6％之间。
[0127]
表6不同故障检测方法在未引入故障的寻优集上的错识率
[0128]
[0129]
5)一级距离模型的多样性分析
[0130]
提出熵测度e来表征参与综合策略的一级距离模型对样本检测的多样性。对于样本集l*，其公式如下：
[0131][0132]
式(15)中，n为单个距离模型个数，nα为样本集l*中所有的样本个数，l(lj)表示样本在n个距离模型中被正确检测的次数。
[0133]
本实施例以在引入故障幅值的寻优集作为样本集。将不同故障幅值下的一级距离模型输出的最大差值距离定义为差值，将其和对应的熵测度e比较用来表征综合距离模型相比于单个距离模型的提升范围及一级距离模型的输出多样性。表7为随机选取的故障幅值下对应得熵测度和差值列表。
[0134]
表7不同幅值下的熵测度及差值
[0135][0136]
表7可以看出熵测度e值和差值在整体上有着一定的相关性，差值较高的故障幅值处其熵测度也较高，这说明在综合距离模型的性能提高的越多的幅值上，其一级距离模型输出的多样性就越丰富。
[0137]
如上即为本发明的实施例。上述实施例以及实施例中的具体参数仅是为了清楚表述发明验证过程，并非用以限制本发明的专利保护范围，本发明的专利保护范围仍然以其权利要求书为准，凡是运用本发明的说明书及附图内容所作的等同结构变化，同理均应包含在本发明的保护范围内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除