一种基于改进型预测控制的CFB锅炉主蒸汽压力控制方法与流程
 2021-02-26 18:02:35|
2021-02-26 18:02:35| 355|
355| 起点商标网
起点商标网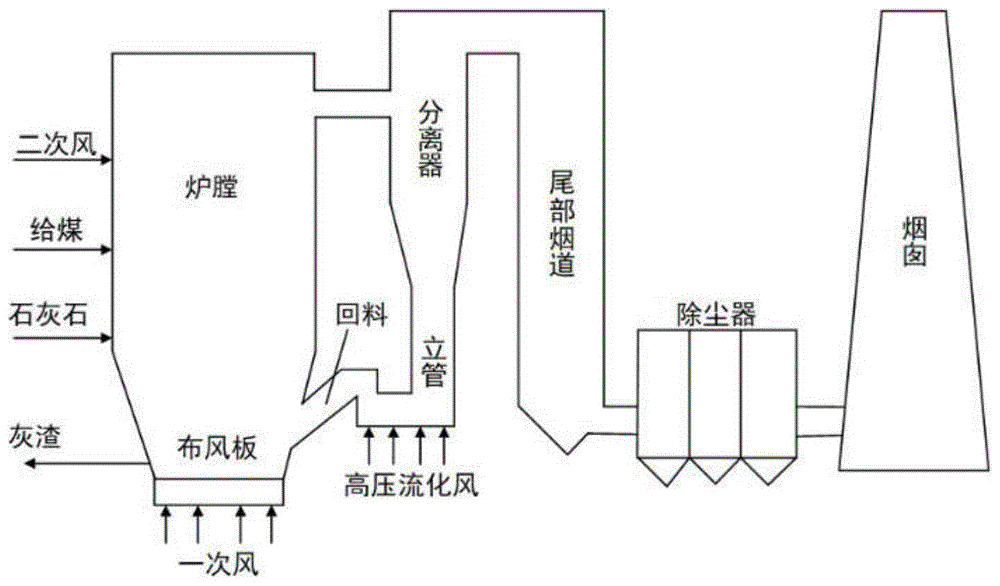
本发明属于控制技术领域,具体涉及一种基于改进型预测控制的cfb锅炉主蒸汽压力控制方法。
背景技术:
近年来,循环流化床(cfb)锅炉受到世界各国的广泛关注从而飞速发展,代替煤粉锅炉成为主流的新型清洁燃烧设备。cfb锅炉因其效率高、占地小、调节性好和低污染等优点而受到肯定。因反复地进行低温燃烧和脱硫,cfb锅炉在运行方式上与传统煤粉锅炉有较大的不同,所以控制方式也存在差异。主蒸汽压力的稳定是保证cfb锅炉安全运行的重要指标之一,因其具有时变性、大惯性、易受外界因素影响等特点,传统的控制方法难以达到预期的效果。
目前,pid控制及其改进方法仍是cfb锅炉主蒸汽压力的主流控制方式,例如二自由度模型驱动的pid控制器,结构简单,易于调整,但控制效果在某些方面仍不太理想。基于模糊控制和模糊自适应的pid控制方法,该类方法有较好的控制品质,但复杂系统的模糊规则和隶属度函数很难选择。基于神经网络模型的cfb锅炉主蒸汽压力控制,耗时过长,计算量大,不易于在工业过程控制中实现。模型预测控制是近年来日趋完善的一类控制策略,在工业系统中得到了成功以及广泛的应用。典型的预测控制算法有:以单位脉冲响应序列为基础的模型算法控制(mac);以单位阶跃响应序列为基础的动态矩阵控制(dmc)和以自回归积分滑动平均模型为基础的广义预测控制(gpc)。以上预测控制方法运用到cfb锅炉主蒸汽压力控制系统,控制效果一定程度上得到了改善,但可调参数少,控制器不灵活。
技术实现要素:
本发明所要解决的技术问题是针对上述现有技术的不足,提供一种基于改进型预测控制的cfb锅炉主蒸汽压力控制方法。
为实现上述技术目的,本发明采取的技术方案为:
一种基于改进型预测控制的cfb锅炉主蒸汽压力控制方法,其中:包括以下步骤:
步骤一:分析cfb锅炉主蒸汽压力控制系统特性及其相应的影响参数,在其他参数不变的情况下,建立主蒸汽压力与燃料量的函数模型g(s);
步骤二:根据k时刻燃料量的实际输入建立arx-laguerre函数模型,计算参数矩阵ay、au、by、bu和c,并根据k时刻主蒸汽压力的实际输出,对参数矩阵c在线辨识,计算k时刻arx-laguerre函数模型输出ym和未来p步主蒸汽压力的理论预测值ym;
步骤三:结合k时刻主蒸汽压力值的实际输出值y,对ym进行误差校正得到校正后的实际预测值
步骤四:根据设定值r和柔化因子β计算参考轨迹矩阵yr;
步骤五:通过实际预测值
步骤六:对第一性能指标j1添加分数阶pid参数,得到改进后的第二性能指标j2,计算最优控制量u*,并将最优控制量作为新的燃煤输入量输入主蒸汽压力与燃料量的函数模型g(s);
步骤七:重复步骤二至步骤六,计算得到下一时刻的最优燃料输入量。
为优化上述技术方案,采取的具体措施还包括:
进一步地,步骤一中,cfb锅炉主蒸汽压力与燃料量的函数关系为
进一步地,步骤二中,建立arx-laguerre函数模型:
其中:x(k+1)为k+1时刻模型的状态矩阵;x(k)为k时刻模型的状态矩阵;a、bu、by、c为模型参数矩阵;u(k)为k时刻燃料量的实际输入值,ym(k)为k时刻的模型输出;
为了避免稳态误差带来的影响,将式(25)改为增量式的状态空间方程,即为:
式中:
δu(k)=u(k)-u(k-1);δym(k)=ym(k)-ym(k-1);
δx(k)=[δx0,y(k),l,δxna-1,y(k),δx0,u(k),l,δxnb-1,u(k)]t;a=diag(ay,au)(na+nb)×(na+nb);
c=[g0,a,l,gna-1,a,g0,b,l,gnb-1,b]t(na+nb)×1;
其中:ξa和ξb为反映系统特性的极点;na和nb为模型参数矩阵的阶次;
利用带遗忘因子的递推最小二乘法对参数矩阵c在线辨识,设辨识模型为δym(k)=δxt(k)c,则辨识方程为:
式中:α为遗忘因子,其值越小,对过早数据遗忘地越快,取0.9到0.99;p(0)=θi,θ为充分大地正实数;δy(k)为实际主蒸汽压力在k时刻的增量。
进一步的,步骤三具体为:
将式(2)的各项展开,得到:
将上式写成矩阵形式,计算得到未来p步主蒸汽压力的理论预测值ym(k+1):
其中:δym(k+1)=ym(k+1)-ym(k);s为单位下三角矩阵;f=[1,1,l,1]tp×1;hl、hu、hy由参数矩阵ay、au、by、bu和c计算得到;
式中:
ym(k+1)=[ym(k+1),ym(k+2),l,ym(k+p)]tp×1
δym(k+1)=[δym(k+1),δym(k+2),l,δym(k+p)]tp×1;
δum(k)=[δu(k),δu(k+1),l,δu(k+m-1)]tm×1;
p为预测步长;m为控制步长;n=na+nb;
由式(5)可得自由响应项为:
yp(k+1)=shlδx(k)+fym(k)(30)
对未来p步的自由响应yp(k+1)进行校正,即为:
式中:y(k)为在k时刻主蒸汽压力的实际输出;
对未来p步主蒸汽压力的理论预测值ym(k+1)进行误差校正得到实际预测值
进一步的,步骤四具体为:
参考轨迹矩阵yr为:
yr(k+1)=[yr(k+1),yr(k+2),l,yr(k+p)]t(33)
其中:yr(k+i)=βiy(k)+(1-βi)r,i=1,2,l,p,β为柔化因子,r为设定值,y(k)为k时刻主蒸汽压力的实际输出。
进一步的,步骤五具体为:
计算实际预测值
计算实际预测值
根据递推原理,可求得δe(k+1)和e(k+1-j),即为:
e(k+1-j)=δ2d(k+1-j)+shuδ3um(k-j)(36)
引入后移算子q-1,可得:
进一步的,步骤六具体为:
取第一性能指标:
式中:q和r分别为误差和输出项的加权矩阵。
分数阶pid算法的表达式为:
u(t)=kpe(t)+kidt-λe(t)+kddtμe(t)(40)
式中:kp、ki和kd为比例、积分和微分参数,λ、μ为积分、微分阶数,
将式(16)写为离散形式,可得:
式中:ts为时间步长,
根据递推原理,可求得u(k-1),即为:
将式(17)与(18)相减,得到增量式分数阶pid的表达式:
令
将第一性能指标即式(15)按式(20)增量式分数阶pid表达式的结构特性进行重新构建,得到改进后的第二性能指标:
将式(13)和(14)代入到式(21)中,并令
令
取控制律的第一项作最优控制量,则有:
并将最优控制量u*(k)作为新的燃煤输入量输入主蒸汽压力与燃料量的函数模型g(s)。
本发明的有益效果:
本发明的一种基于改进型预测控制的cfb锅炉主蒸汽压力控制方法,该方法与传统的控制方法相比,具有响应速度快、无超调、跟踪性能好、鲁棒性强的优点,提高了系统的各项响应特性,通过预测控制与分数阶pid控制相结合的方式,有效解决了传统控制策略下cfb锅炉主蒸汽压力难以实现精确控制的问题。
附图说明
图1为cfb锅炉系统示意图;
图2为控制系统原理图;
图3为almpcfopid算法与lmpc、fopid算法下cfb锅炉主蒸汽压力响应比较图;
图4为almpcfopid算法与lmpc、fopid算法下cfb锅炉主蒸汽压力跟踪比较图;
图5为给定扰动下almpcfopid算法与lmpc算法的系统响应比较图;
图6为模型失配下almpcpid算法在失配前后的系统响应比较图。
具体实施方式
以下结合附图对本发明的实施例作进一步详细描述。
如图2所示,本发明为一种基于改进型预测控制的cfb锅炉主蒸汽压力控制方法,其中:包括以下步骤:
步骤一:分析cfb锅炉主蒸汽压力控制系统特性及其相应的影响参数,在其他参数不变的情况下,建立主蒸汽压力与燃料量的函数模型g(s);
其中步骤一中的主蒸汽压力与燃料量的函数关系为
步骤二:根据k时刻燃料量的实际输入建立arx-laguerre函数模型,计算参数矩阵ay、au、by、bu和c,并根据k时刻主蒸汽压力的实际输出,对参数矩阵c在线辨识,计算k时arx-laguerre函数模型输出ym和未来p步主蒸汽压力的理论预测值ym;
具体为:建立arx-laguerre函数模型:
其中:x(k+1)为k+1时刻模型的状态矩阵;x(k)为k时刻模型的状态矩阵;a、bu、by、c为模型参数矩阵;u(k)为k时刻燃料量的实际输入值,ym(k)为k时刻的模型输出;
为了避免稳态误差带来的影响,将式(49)改为增量式的状态空间方程,即为:
式中:
δu(k)=u(k)-u(k-1);δym(k)=ym(k)-ym(k-1);
δx(k)=[δx0,y(k),l,δxna-1,y(k),δx0,u(k),l,δxnb-1,u(k)]t;a=diag(ay,au)(na+nb)×(na+nb);
c=[g0,a,l,gna-1,a,g0,b,l,gnb-1,b]t(na+nb)×1;
其中:ξa和ξb为反映系统特性的极点;na和nb为模型参数矩阵的阶次;
利用带遗忘因子的递推最小二乘法对模型参数矩阵c在线辨识,设辨识模型为δym(k)=δxt(k)c,则辨识方程为:
式中:α为遗忘因子,其值越小,对过早数据遗忘地越快,取0.9到0.99;p(0)=θi,θ为充分大地正实数;δy(k)为实际主蒸汽压力在k时刻的增量。
步骤三:结合k时刻主蒸汽压力的实际输出值y,对ym进行误差校正得到校正后的实际预测值
具体为:将式(2)的各项展开,得到:
将式(4)写成矩阵形式,计算得到未来p步主蒸汽压力的理论预测值ym(k+1):
其中:δym(k+1)=ym(k+1)-ym(k);s为单位下三角矩阵;f=[1,1,l,1]tp×1;hl、hu、hy由参数矩阵ay、au、by、bu和c计算得到;
式中:
ym(k+1)=[ym(k+1),ym(k+2),l,ym(k+p)]tp×1
δym(k+1)=[δym(k+1),δym(k+2),l,δym(k+p)]tp×1;
δum(k)=[δu(k),δu(k+1),l,δu(k+m-1)]tm×1;
其中:p为预测步长;m为控制步长;n=na+nb。
由式(5)可得自由响应项为:
yp(k+1)=shlδx(k)+fym(k)(54)
对未来p步的自由响应yp(k+1)进行校正,即为:
式中:y(k)为在k时刻主蒸汽压力的实际输出;
对未来p步主蒸汽压力的理论预测值ym(k+1)进行误差校正得到实际预测值
步骤四:根据设定值r和柔化因子β计算参考轨迹矩阵yr;
具体为:参考轨迹矩阵yr为:
yr(k+1)=[yr(k+1),yr(k+2),l,yr(k+p)]t(57)
其中:yr(k+i)=βiy(k)+(1-βi)r,i=1,2,l,p,β为柔化因子,r为设定值,y(k)为k时刻主蒸汽压力的实际输出。
步骤五:通过实际预测值
具体为:计算实际预测值
计算实际预测值
根据递推原理,可求得δe(k+1)和e(k+1-j),即为:
e(k+1-j)=δ2d(k+1-j)+shuδ3um(k-j)(60)
引入后移算子q-1,可得:
步骤六:对第一性能指标j1添加分数阶pid参数,得到改进后的第二性能指标j2,计算最优控制量u*,并将最优控制量作为新的燃煤输入量输入主蒸汽压力与燃料量的函数模型g(s);
具体为:取第一性能指标:
式中:q和r分别为误差和输出项的加权矩阵。
分数阶pid算法的表达式为:
u(t)=kpe(t)+kidt-λe(t)+kddtμe(t)(64)
式中:kp、ki和kd为比例、积分和微分参数,λ、μ为积分、微分阶数,
将式(16)写为离散形式,可得:
式中:ts为时间步长,
根据递推原理,可求得u(k-1),即为:
将式(17)与(18)相减,得到增量式分数阶pid的表达式:
令
将第一性能指标即式(15)参照式(20)增量式分数阶pid表达式的结构进行重新构建,得到改进后的第二性能指标:
将式(13)和(14)代入到式(21)中,并令
令
取控制律的第一项作最优控制量,则有:
并将最优控制量u*(k)作为新的燃煤输入量输入主蒸汽压力与燃料量的函数模型g(s)。
步骤七:重复步骤二至步骤六,计算得到下一时刻的最优燃料输入量。
本发明为一种基于改进型预测控制的cfb锅炉主蒸汽压力控制方法,其控制效果如图3至图6所示:
主蒸汽压力的设定值作瞬时变化时的系统响应曲线如图3所示,将本方法利用的基于arx-laguerre函数模型的分数阶pid预测控制策略,即almpcfopid算法与现有的lmpc算法和常规fopid算法进行横向比对,由图3可以看出,三种算法都能满足控制要求,但本方法的调节时间在500s左右,且无超调,响应速度上更具优势。
进一步验证算法的跟踪性能,图4给出了当设定值不断变化时,almpcfopid算法与lmpc算法的系统响应曲线对比图,由图4可以看出,本方法在设定值作连续变化时仍能保持优秀的性能,跟踪能力要优于lmpc算法。
当系统处在稳定的工作状态时,我们在3000s处加入一个大小为0.1mpa的瞬时扰动,将扰动下almpcfopid算法和lmpc算法的响应曲线作比较,得到如图5所示的对比图,可以看出,本方法能快速对扰动作出响应,与lmpc算法相比,波动大小相当,但本方法的恢复时长更短,一定程度上提高了系统抗外界干扰的能力。
实际系统中,存在多种外部因素可导致系统模型发生改变,从而使比例和惯性时间常数产生变化。改变对象模型模拟模型失配的情况,如图6所示,本方法依旧能保证系统逼近设定值,仅出现略微超调,说明了本方法具有较强的自适应能力。
以上仅是本发明的优选实施方式,本发明的保护范围并不仅局限于上述实施例,凡属于本发明思路下的技术方案均属于本发明的保护范围。应当指出,对于本技术领域的普通技术人员来说,在不脱离本发明原理前提下的若干改进和润饰,应视为本发明的保护范围。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



