一种燃气锅炉温度控制方法与流程

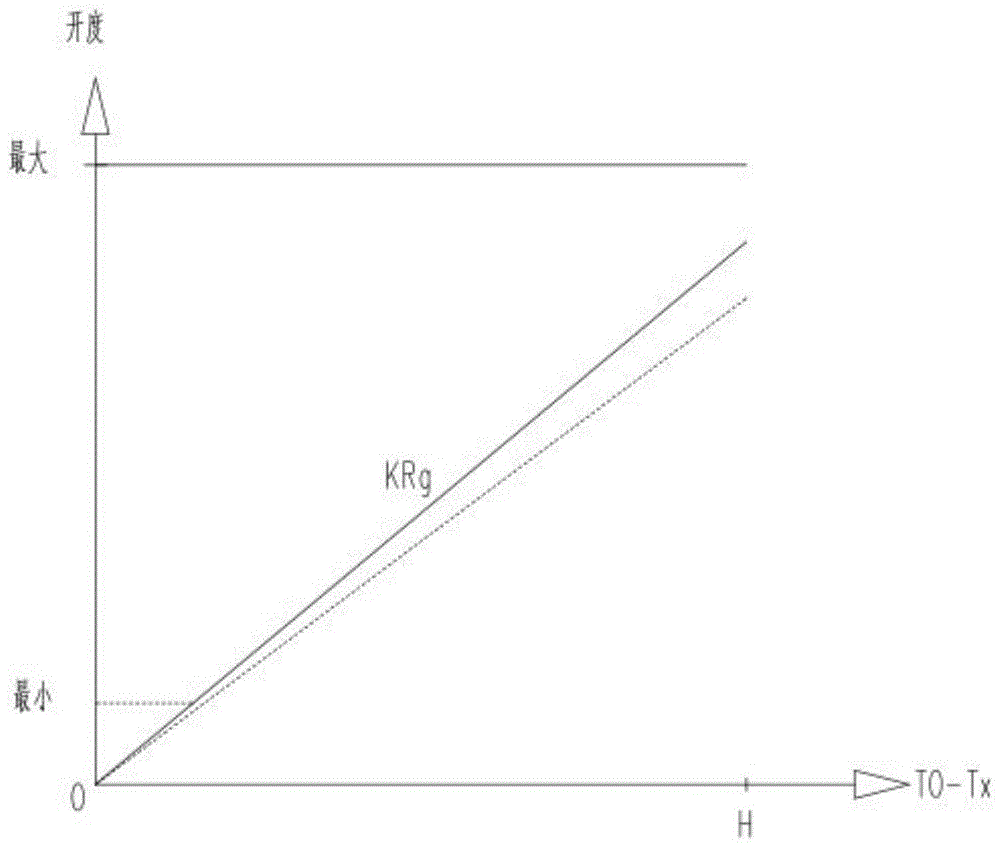
本发明涉及自动化控制技术领域，尤其涉及一种燃气锅炉温度控制方法。

背景技术：

pid调节是自动化控制领域常用的方法，pid调节的曲线是开始过冲较大，随后围绕目标值上下波动并逐步靠近目标值。

锅炉是一个大滞后的系统，无论被加热介质是水还是蒸汽，再加上炉膛结构、热交换效率、散热损失等多种原因，造成被加热介质的温度难于控制，很多时候，p、i、d值很难给定，这一调试过程很漫长，以至于很多新手会放弃。

一方面是对各种调节阀的特性掌握；二方面是对被控对象工况的充分了解，造成现场pid的调试费时费力，很多老专家都费劲，更何况新手。

技术实现要素：

本发明旨在解决现有技术的不足，而提供一种燃气锅炉温度控制方法。

本发明为实现上述目的，采用以下技术方案：一种燃气锅炉温度控制方法，其特征在于，其步骤包括：

一、建立数学模型

(1)燃气锅炉燃烧器功率调节原理

在其它条件不变的情况下，燃气流量与燃气阀门开度的关系可以表示为：

燃气流量＝系数*燃气阀门开度

即可以通过调节燃气阀的开度大小来调节燃烧器的输出功率的大小；

当设定一个目标温度后，燃气阀开度开到最大，即系统开始持续大火(大功率输出)，持续升温过程；当采集到的实时温度接近目标温度时，火焰逐渐变小；

距目标温度越近，燃气阀开度越小，直到稳定在目标温度附近(小于系统允许的精度)时，保持燃气阀开度，即到了保温阶段；

(2)根据燃气锅炉燃烧器功率调节原理建立温度控制模型

a定义参数

t-------计时器(秒)；

t0------目标温度℃(可设定)；

tx1～tx10----实时温度采集值；

tx-----实时温度采集值的平均值，即tx＝(tx1+tx2+…tx10)/10；

tma----温度上限(可设定)；

tmn----温度下限(可设定)；

kr2-----燃气阀最大开度(可设定，初始值90)；

kr1-----燃气阀最小开度(可设定，初始值5)；

krx----实时燃气阀开度(反馈值，范围0～100)；

kfx----实时风门阀开度(反馈值，范围0～100)；

krg----燃气阀开度给定值(计算得出的，初始值0，范围0～100)；

kfg-----风门阀开度给定值(计算得出的，初始值50，范围0～100)；

krf-----燃气调节阀开度与风门调节阀开度的比例系数(可设定，初始值1.0，范围0.1～1.9)，燃气阀与风门都是蝶阀时，krf是个常数，其它阀krf是变数，通过试验测得的数据查表获取krf；

d----响应时间(可设定，范围30～900秒)；

h----调整幅度(可设定，范围大于1的整数)；

hs---微调升温速率(可设定，范围1～2之间的正数)。

b建模

在设定一个目标温度t0后，燃气阀开度开到最大，即系统开始持续大火(大功率输出)，持续升温过程；当采集到的实时温度tx接近目标温度t0，即(t0-tx)<＝h时，开始降低输出功率；

即随着(t0-tx)逐步减小，同步减小燃气阀开度，缓慢接近目标温度t0；当(t0-tx)小于系统允许的精度时，保持燃气阀开度，说明到了保温阶段。

出现二种情况：

一种是：虽然到目标温度后保持小火(功率)输出，仍过冲，说明升温速度太快，需调整升温速率；

另一种是：一直不能到达系统目标温度，说明升温速度太慢了，需调整升温速率；

调整升温速率仍不能稳定在目标温度时，需要重新设置参数h；

由此得出，最直观的算法如下：

燃气阀开度krg＝燃气阀最大开度*升温速率*温差比例。

即得出，数学模型1：krg＝kr2*hs*(t0-tx)/h

但这里的hs的范围应改为小于1的正数了,0.1～0.99；数值越大阀门开度越大,升温越快；h的定义不变；

基于数学模型1,可以得到阀门开度与(t0-tx)的关系；

从中可以看出问题：

尽管可以调整h和升温速率hs，也只能改变这条斜线的斜率，其原点始终是零，即当(t0-tx)＝0时，计算出阀门开度为零，即阀门处于关闭状态；

那就只能在(t0-tx)接近或等于0时，即算出的阀门开度小于阀门初始设定的最小开度值时，强制为最小开度值；这两种情况都会造成温度波动大，系统始终波动，很难稳定在目标值上，更难于到达系统精度要求，实施过程调整控制流程也不能改变数学模型1的特性；

为达到较稳定地控制温度的目的，用(h-(t0-tx))同样可以表达出温度控制的原理，随着实时采集的温度tx接近目标值t0的变化过程，只不过(h-(t0-tx))由小到大，(t0-tx)/h是由大到小。

因此建立新的数学模型2：

数学模型2：krg＝kr2/(hs+h-(t0-tx))；

h仍然是调整幅度，同时对升温速率影响较大；hs是微调升温速率；

其应用效果下：

当h设置太大了，不仅意味着过早进入调节阶段，调节时间拉长，而且tx越接近t0时，燃气阀门开度krg快速变小，即燃烧器输出功率快速变小，被加热介质升温速度快速减慢，可能很长时间或永不能到达目标值时(因锅炉都有散热损失)；

当h设置太小了，不仅意味着调节时间变短，而且tx越接近t0时，燃气阀门开度krg缓慢变小，即燃烧器输出功率缓慢变小，被加热介质升温速度缓慢降低，很有可能过冲；

即使小幅改变hs(作用是微调)，也很难改变上述两个过程；这就要求对被控对象有一定了解，而且，还需要通过编程来控制；

即粗略估计出三个设定值d、h、hs后，在系统运行过程中，通过程序来自动调整h和hs值，进一步优化这两个参数，使系统尽快稳定在目标值上；

数学模型2为燃气锅炉温度控制方法最终确认的数学模型。

二、模型实施

(1)参数设置重新定义

d----响应时间(可设定，范围30～600秒，如在升温段估算升温0.5度需要的时间，这样控制精度可以提高；负荷越大升降温速度越慢)；

h----调整幅度或负荷值(可设定，范围1～9的整数，根据炉子实际负荷确定，负荷越大降温越快升温越慢，需要功率大，数值越小)；

hs---微调升温速率(可设定，范围1.1～1.9；数值越小升温越快；降温速度由锅炉决定，不用考虑)；

cg------中间值，阶段标志；(初始值0，0升温段；1到达；2过冲了)；

cw------中间值，未到达过目标计数；(初始值0，未到过目标)；

cwg-----中间值，初值为1，范围1～9；过冲时计数，因为在高温时，热容大，不但升温慢降温速度也慢；

cwm-----中间值，是cw的最大值，计算得出温度从tx到t0需要经过多少次d调节周期，再乘个系数1.5倍(冗余度)，超过这个值表示长时不能到目标温度；

这个参数的设置是为了防止由于d、h、hs三个参数设置不当，造成系统长时间不能到达目标值，无限期等待；

cwm＝(d/60)*1.5*h；取整数；

精度说明:用(t0/tx)表示，在这里为达到1％的控制精度要求，(t0/tx)应控制在0.98～1.01范围内，可根据目标温度和精度要求调整。

(2)具体实施

①自动循环显示、安全检测和报警处理；

cwm＝(d/60)*1.5*h；

当tx-tma>＝0时，krg＝kr1；kfg＝krf*krg，超高温报警；跳转到①；

当tx-tmn<＝0且cg＝1时，则krg＝kr2；kfg＝krf*krg，超低温报警；跳转到①；

当t<d时跳转到①；

②当(t0-tx)>h(未到调节段)，krg＝kr2保持大火；kfg＝krf*krg跳转到①；

③当(t0/tx)>1.01(已进入调节段但未到目标值)，跳转到⑦；

④当(t0/tx)>0.98且cg＝0时，则cg＝1；刚到目标值，保持开度；跳转到①；

当(t0/tx)>0.98且cg＝1时，则已在目标值，保持当前开度；跳转到①；

当(t0/tx)>0.98且cg＝2时，则cg＝1；回到目标值，保持开度；跳转到①；

⑤温度已过冲，则cg＝2且cwg＝cwg+1；

当cwg>3时则cwg＝1且hs＝hs+0.1；当hs>1.9时，则hs＝1.1且h＝h+1；

当h>9时则h＝9；

⑥跳转到⑨

⑦在调节段，当cg＝0时则cw＝cw+1；

⑧当cw>cwm时则cw＝0且hs＝hs-0.1；当hs＝1.0时则hs＝1.1且h＝h-1；当h＝0时则h＝1；说明长时间不能升到目标值；

⑨这时燃气阀开度krg＝kr2/(hs+h-(t0-tx))；kfg＝krf*krg；跳转到①；

本发明h能自动调整，参数设置可以比较随意，但正因为h值能自动调整，使得温度控制曲线和pid调节算法的曲线差不多，过冲大而且会长时间围绕目标值上下波动，温度很难在短时间内稳定在目标值要求精度之内；

因此，在实际应用中，在人工设置合适的h后，考虑到过冲值不应很大，在控制流程中也可以去掉过冲段自动调整h，只自动调整hs，有时也需要调整cwg的最大限值，不会产生大幅上下波动，系统能很快稳定；

改动如下:

⑤温度已过冲，则cg＝2且cwg＝cwg+1；

当cwg>2时，则cwg＝1且hs＝hs+0.1；当hs>1.9时，则hs＝1.1；

通过程序控制可以实现:当负荷波动造成实时采集的温度偏离目标值时，系统会自动调整阀门开度，最后都能稳定在目标值上，保证在系统要求精度之内。

本发明的有益效果是：负荷正常波动不影响控制精度；通俗易懂，易于理解和掌握，有点常识的技术人员都可以做到，到现场调试半天时间就可以实现温度自动控制，省时省力。

附图说明

图1为数学模型1燃气阀门开度与(t0-tx)的关系图；

图2为数学模型2燃气阀门开度与(t0-tx)的关系图；

图3为长时间不能到达目标值的温度变化曲线图；

图4为过冲温度变化曲线图；

以下将结合本发明的实施例参照附图进行详细叙述。

具体实施方式

下面结合附图和实施例对本发明作进一步说明：

如图1-4所示，一种燃气锅炉温度控制方法，其特征在于，其步骤包括：

一种燃气锅炉温度控制方法，其特征在于，其步骤包括：

一、建立数学模型

(1)燃气锅炉燃烧器功率调节原理

在其它条件不变的情况下，燃气流量与燃气阀门开度的关系可以表示为：

燃气流量＝系数*燃气阀门开度

当燃气阀是蝶阀时，燃气流量与阀门开度是线性关系，“系数”是常数，其它种阀则是非线性关系，“系数”就是个变量，这里暂不作详细讨论，只要知道，燃气阀的开度越大，流量越大就行了；反之亦然；

即可以通过调节燃气阀的开度大小来调节燃烧器的输出功率的大小；

当设定一个目标温度后，燃气阀开度开到最大，即系统开始持续大火(大功率输出)，持续升温过程；当采集到的实时温度接近目标温度时，火焰逐渐变小；

距目标温度越近，燃气阀开度越小，直到稳定在目标温度附近(小于系统允许的精度)时，保持燃气阀开度，即到了保温阶段；

(2)根据燃气锅炉燃烧器功率调节原理建立温度控制模型

a定义参数

t-------计时器(秒)；

t0------目标温度℃(可设定)；

tx1～tx10----实时温度采集值；

tx-----实时温度采集值的平均值，即tx＝(tx1+tx2+…tx10)/10；

tma----温度上限(可设定)；

tmn----温度下限(可设定)；

kr2-----燃气阀最大开度(可设定，初始值90)；

kr1-----燃气阀最小开度(可设定，初始值5)；

krx----实时燃气阀开度(反馈值，范围0～100)；

kfx----实时风门阀开度(反馈值，范围0～100)；

krg----燃气阀开度给定值(计算得出的，初始值0，范围0～100)；

kfg-----风门阀开度给定值(计算得出的，初始值50，范围10～100)；

krf-----燃气调节阀开度与风门调节阀开度的比例系数(可设定，初始值1.0，范围0.1～1.9)，燃气阀与风门都是蝶阀时，krf是个常数，其它阀krf是变数，都可以查表(试验测得的数据)获取krf；

d----响应时间(可设定，范围30～900秒)；

h----调整幅度(可设定，范围大于1)；

hs---微调升温速率(可设定，范围1～2之间的正数)。

b建模

在设定一个目标温度t0后，燃气阀开度开到最大，即系统开始持续大火(大功率输出)，持续升温过程；当采集到的实时温度tx接近目标温度t0，即(t0-tx)<＝h时，开始降低输出功率；

即随着(t0-tx)逐步减小，同步减小燃气阀开度，缓慢接近目标温度t0；当(t0-tx)小于系统允许的精度时，保持燃气阀开度，说明到了保温阶段。

出现二种情况：

一种是：虽然到目标温度后保持小火(功率)输出，仍过冲，说明升温速度太快，需调整升温速率；

另一种是：一直不能到达系统目标温度，说明升温速度太慢了，需调整升温速率；

调整升温速率仍不能稳定在目标温度时，需要重新设置参数h；

由此得出，最直观的算法如下：

燃气阀开度krg＝燃气阀最大开度*升温速率*温差比例。

当hs<1；初始值0.8，范围0.1～0.9，数值越大升温越快；

设定值h>1；初始值5；

(t0-tx)>0；

即得出，数学模型1：krg＝kr2*hs*(t0-tx)/h

但这里的hs的范围应改为小于1的正数了,0.1～0.99；数值越大阀门开度越大,升温越快；h的定义不变；

基于数学模型1,可以得到阀门开度与(t0-tx)的关系图,如图1；

从中可以看出问题：

尽管可以调整h和升温速率hs，也只能改变这条斜线的斜率，其原点始终是零，即当(t0-tx)＝0时，计算出阀门开度为零，即阀门处于关闭状态；

那就只能在(t0-tx)接近或等于0时，即算出的阀门开度小于阀门初始设定的最小开度值时，强制为最小开度值；这两种情况都会造成温度波动大，系统始终波动，很难稳定在目标值上，更难于到达系统精度要求，实施过程调整控制流程也不能改变数学模型1的特性；

为达到较稳定地控制温度的目的，需要换一个思路，用(h-(t0-tx))同样可以表达出温度控制的原理，随着实时采集的温度tx接近目标值t0的变化过程，只不过(h-(t0-tx))由小到大，(t0-tx)/h是由大到小。

因此建立新的数学模型：

数学模型2：krg＝kr2/(hs+h-(t0-tx))；

h仍然是调整幅度，同时对升温速率影响较大；hs是微调升温速率；

因算法改变，需要对有些参数在实施过程重新定义。

基于数学模型2，得出阀门开度与(t0-tx)的关系图，如图2；

这个数学模型只有一个除法，更简单、易于处理，更符合实际温度变化规律。

其应用效果下：

当h设置太大了，不仅意味着过早进入调节阶段，调节时间拉长，而且tx越接近t0时，燃气阀门开度krg快速变小，即燃烧器输出功率快速变小，被加热介质升温速度快速减慢，可能很长时间或永不能到达目标值时(因锅炉都有散热损失)；

当h设置太小了，不仅意味着调节时间变短，而且tx越接近t0时，燃气阀门开度krg缓慢变小，即燃烧器输出功率缓慢变小，被加热介质升温速度缓慢降低，很有可能过冲；

即使小幅改变hs(作用是微调)，也很难改变上述两个过程；这就要求对被控对象有一定了解，而且，还需要通过编程来控制；

即粗略估计出三个设定值d、h、hs后，在系统运行过程中，通过程序来自动调整h和hs值，进一步优化这两个参数，使系统尽快稳定在目标值上；

数学模型2为燃气锅炉温度控制方法最终确认的数学模型。

二、模型实施

(1)参数设置重新定义

d----响应时间(可设定，范围30～600秒，如在升温段估算升温0.5度需要的时间，这样控制精度可以提高；负荷越大升降温速度越慢)；

h----调整幅度或负荷值(可设定，范围1～9的整数，根据炉子实际负荷确定，负荷越大降温越快升温越慢，需要功率大，数值越小)；

hs---微调升温速率(可设定，范围1.1～1.9；数值越小升温越快；降温速度由锅炉决定，不用考虑)；

cg------中间值，阶段标志；(初始值0，0升温段；1到达；2过冲了)；

cw------中间值，未到达过目标计数；(初始值0，未到过目标)；

cwg-----中间值，初值为1，范围1～9；过冲时计数，因为在高温时，热容大，不但升温慢降温速度也慢；

cwm-----中间值，是cw的最大值，计算得出温度从tx到t0需要经过多少次d调节周期，再乘个系数1.5倍(冗余度)，超过这个值表示长时不能到目标温度；

这个参数的设置是为了防止由于d、h、hs三个参数设置不当，造成系统长时间不能到达目标值，无限期等待；

cwm＝(d/60)*1.5*h；取整数；

精度说明:为达到1％的精度要求，用(t0/tx)表示，其范围0.98～1.01，可根据介质温度范围和精度要求调整。

(2)具体实施

①自动循环显示、安全检测和报警处理；

cwm＝(d/60)*1.5*h；

当tx-tma>＝0时，krg＝kr1；kfg＝krf*krg，超高温报警；跳转到①；

当tx-tmn<＝0且cg＝1时，则krg＝kr2；kfg＝krf*krg，超低温报警；跳转到①；

当t<d时跳转到①；

②当(t0-tx)>h(未到调节段)，krg＝kr2保持大火；kfg＝krf*krg跳转到①；

③当(t0/tx)>1.01(已进入调节段但未到目标值)，跳转到⑦；

④当(t0/tx)>0.98且cg＝0时，则cg＝1；刚到目标值，保持开度；跳转到①；

当(t0/tx)>0.98且cg＝1时，则已在目标值，保持当前开度；跳转到①；

当(t0/tx)>0.98且cg＝2时，则cg＝1；回到目标值，保持开度；跳转到①；

⑤温度已过冲，则cg＝2且cwg＝cwg+1；

当cwg>3时则cwg＝1且hs＝hs+0.1；当hs>1.9时，则hs＝1.1且h＝h+1；

当h>9时则h＝9；

⑥跳转到⑨

⑦在调节段，当cg＝0时则cw＝cw+1；

⑧当cw>cwm时则cw＝0且hs＝hs-0.1；当hs＝1.0时则hs＝1.1且h＝h-1；当h＝0时则h＝1；说明长时间不能升到目标值；

⑨这时燃气阀开度krg＝kr2/(hs+h-(t0-tx))；kfg＝krf*krg；跳转到①；

本发明h能自动调整，参数设置可以比较随意，但正因为h值能自动调整，使得温度控制曲线和pid调节算法的曲线差不多，过冲大而且会长时间围绕目标值上下波动，温度很难在短时间内稳定在目标值要求精度之内；

因此，在实际应用中，在人工设置合适的h后，考虑到过冲值不应很大，在控制流程中也可以去掉过冲段自动调整h，只自动调整hs，有时也需要调整cwg的最大限值，不会产生大幅上下波动，系统能很快稳定；

改动如下:

⑤温度已过冲，则cg＝2且cwg＝cwg+1；

当cwg>2时，则cwg＝1且hs＝hs+0.1；当hs>1.9时，则hs＝1.1；

通过程序控制可以实现:当负荷波动造成实时采集的温度偏离目标值时，系统会自动调整阀门开度，最后都能稳定在目标值上，保证在系统要求精度之内。

两种情况的应用实例如下：

一、长时间不能到达目标值实例

在一台10吨热水炉上应用，进口水温16.3℃。

首先，通过面板设置参数如下:

t0-----目标温度为95℃；

tma----温度上限99℃；

tmn----温度下限92℃；

d------响应时间，设定初始值120秒，即升温0.5度大概需要180秒；

h------调整幅度或负荷值，设定初始值为7；

hs-----微调升温速率，设定初始值为1.5；

系统精度要求:1％。

应用上述算法和控制流程，运行结果如下:

燃烧器运行4小时后，温度刚到91.2℃；

燃烧器运行8小时后，温度刚到92.5℃；

燃烧器运行12小时后，温度刚到93.2℃；

燃烧器运行15小时后，温度才到93.4℃；

燃烧器运行23小时后，温度才到93.7℃；

因为在升温段这个过程没有出现超温报警，但等待时间太长，说明参数设置的不合适。虽然程序控制中在不断自我调整，自动减小hs，进而减小h值，但过程很慢。

重新设置参数h＝5，hs＝1.3；在1多小时后，水温到达94.6℃；之后一直维持在95℃附近。

温度变化曲线，如见图3。

二、过冲实例

在另一台10吨热水炉上应用，使用同样的燃烧器，进口水温17.7℃。

通过面板设置参数如下:

t0-----目标温度为95℃；

tma----温度上限99℃；

tmn----温度下限92℃；

d------响应时间，设定初始值120秒，即升温0.5度大概需要180秒；

h------调整幅度或负荷值，设定初始值为3；

hs-----微调升温速率，设定初始值为1.3；

系统精度要求:1％。

应用上述算法和控制流程，运行结果如下:

燃烧器运行3小时后，温度到92.5℃；

燃烧器运行4小时后，温度到97.6℃；

燃烧器运行5小时后，温度到95.7℃；

燃烧器运行6小时后，温度到95.3℃；

水温很快到达目标值附近，说明参数设置的合适。

此后几天，我们把hs初始值调到1.6，即微调在调节段的燃气阀开度(略微减小输出功率)，重新开始，发现过冲温度最高值降到了96.3℃。这可以进一步降低过冲量，缩短系统稳定时间，实现系统优化。

用这个方法实现温度自动控制，也会有过冲现象，但经过几个回合的自我调整，会很快稳定在目标温度。

温度变化曲线，如见图4。

关于参数初始值现场设置说明

d----一般都能知道这台炉子1小时大概能升温多少度，以此推算d值应设为多少，如1小时能升温30℃，那么d应设为60(秒)或稍大一些。

h----对于10吨10吨热水锅炉，实际要把10吨水加热到90℃，那么h应设为3或2。但是，如果对于10吨热水锅炉，实际要把7吨水加热到90℃，或把10吨水加热到70℃，那么h应设为8或7。hs应设在1.2～1.5之间。

从实践中总结出，现场调试的原则:

d----稍微偏大些，h----偏小些，这样开始就过冲一些，可以尽快稳定，缩短调试时间。

本发明适用于所有可连续调节输出功率的燃气/燃油锅炉温度自动控制系统和电加热炉的温度自动控制系统。

上面结合附图对本发明进行了示例性描述，显然本发明具体实现并不受上述方式的限制，只要采用了本发明的方法构思和技术方案进行的各种改进，或未经改进直接应用于其它场合的，均在本发明的保护范围之内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除