基于数据驱动的余热锅炉阀门自适应调节方法与流程

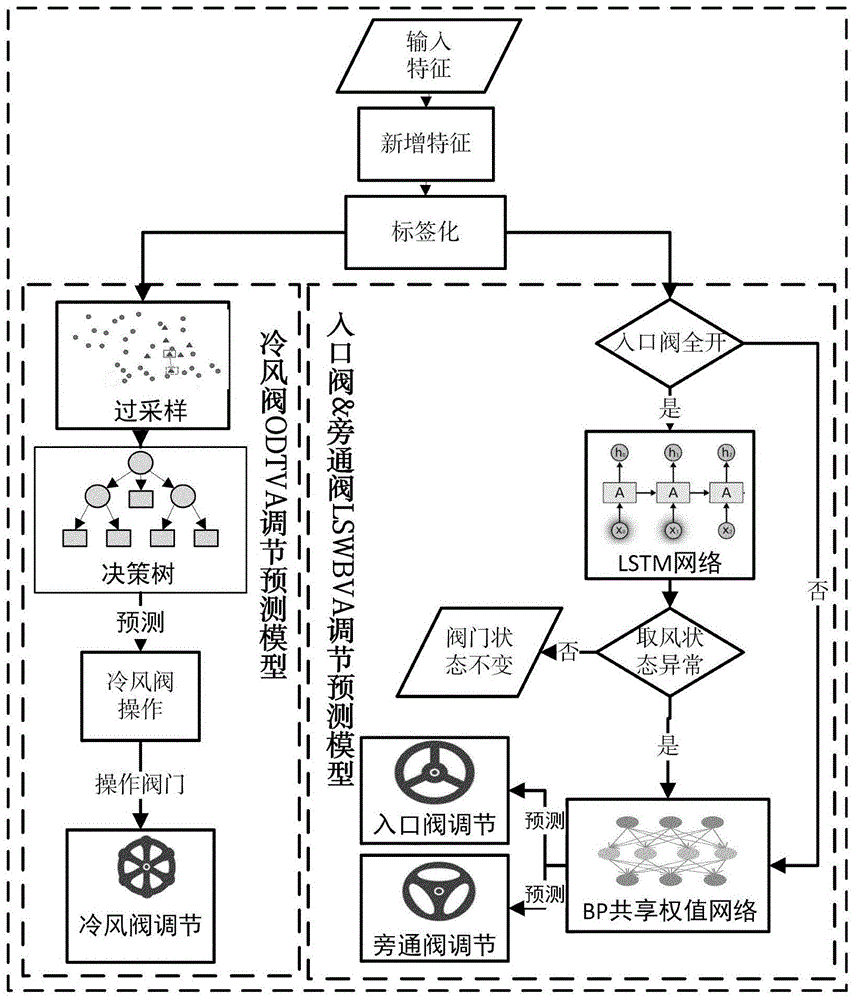
本发明涉及水泥生产余热发电领域，具体涉及基于数据驱动的余热锅炉阀门自适应调节方法。

背景技术：

近年来，随着社会经济的发展，我国水泥行业产量迅速提升。根据数据表明，2014年我国的水泥产量在全球的总产量占比为56.7％。同时，水泥行业又是一个典型的高能耗产业，水泥行业的能耗在全球能源消耗占比为8.5％，并且二氧化碳的排放量占比高达34％。

水泥生产过程中，熟料煅烧过程占水泥生产总能耗92.6％以上，然而其中只有大约60％的热量被熟料煅烧所利用，剩余的40％热量随着窑头、窑尾的废气一起排入到了大气中。不但造成了大气污染，还造成了大量热能的损耗。余热发电技术作为一种新兴技术，有效的解决了水泥生产中余热能源浪费的问题，因此如何提升能源利用率成为余热发电系统的关键性问题。目前，低温余热发电技术的系统优化方法可以分为两类，基于专家经验的系统控制优化，以及基于数据驱动的系统控制优化。

基于专家经验的系统控制优化常用模糊控制等手段。其主要利用生产现场的工作人员的控制经验为基础，从系统控制方面进行优化。其中，文献[z.wang,z.yu,s.guoandx.li,"fuzzypidcontrolappliedinevaporatoroforganicrankinecyclesystem,2019]以有机朗肯循环系统中的蒸发器为研究对象，使用模糊pid控制，使系统具有更好的稳定性。文献[l.silva-llanca,c.v.ponce,m.arayaanda.j.díaz,"optimizationofanorganicrankinecyclethroughacontrolstrategyforwasteheatrecovery,2018]使用pid控制器将涡轮机入口条件保持在过热状态，而没有明显的过冲现象，提高了系统的热效率。文献[农小杰,汪安逸,赵月.柳钢烧结余热发电优化控制系统的设计及应用[c].2015]结合专家控制系统为汽轮机调控操作提供专家指导建议,优化烧结余热发电的生产控制水平,最终达到提高发电量的目的。上述方法虽然取得了较好的效果，但是该方法无法对系统各个参数之间的内部关系进行深度挖掘，且无法应对工业场景的复杂性。

近年来，iot技术被广泛应用于工业领域，在物联网技术的加持下，设备产生了海量的运行数据。基于数据驱动的系统控制优化成为了一种主流研究方法。其主要通过深度挖掘历史数据之间的内在关系，来不断的调整优化设备参数。常用的方法有神经网络，遗传算法等。其中，文献[王正,姚光伟.基于bp神经网络低温余热发电系统建模[j].能源研究与管理,2014(04):29-32.]研究涡轮机转速与工质蒸发压力对于涡轮机输出功率的影响的问题，将bp神经网络应用于低温余热系统建模中，证明了基于bp神经网络模型在建模中有效性。文献[刘强,付文成,尚小科.基于bp神经网络策略的中低温余热发电系统性能优化[j].化工管理,2019(01):109-110.]采用基于神经网络的pid控制方法对中低温余热发电系统中的膨胀机动态性能进行了调节，证明与传统pid控制相比,该算法具有较好的控制效果。文献[g.n.g.alcoforado,v.b.deoliveira,g.m.dealmeidaandm.a.desouzaleitecuadros,"amodelofprocesssteamnetworkinasteelplantwithidentificationofparametersbyageneticalgorithm,2016]利用遗传算法，提出了一个蒸汽网络模型，该模型可以减小蒸汽质量平衡的不稳定性和蒸汽能量损失，提高能源利用率。

技术实现要素：

传统余热锅炉阀门主要通过模糊控制等技术进行人工调节。针对余热锅炉阀门调节影响因素众多，参数关系复杂等问题，提出了基于数据驱动的余热锅炉阀门自适应调节方法，该方法分为以下分为两个子模型：首先通过数据预处理，挖掘阀门调节与余热锅炉特征参数的内在联系，构建了冷风阀odtva调节预测模型(oversampling-baseddecisiontreecoolingairvalveadjustmentpredictionmodel，简称odtva调节预测模型)。其次，针对入口阀和旁通阀两者调节依赖时序性特征且强相关性等问题，构建了入口阀&旁通阀lswbva调节预测模型(predictionmodelofinletvalveandbypassvalveadjustmentbasedonlstm-bpsharedweightneuralnetwork，简称lswbva调节预测模型)。根据以上方法，将阀门调节数据转换为调节模型，替代人工调节，可以有效解决企业的人力成本，并且保证锅炉调节稳定性和安全性。

为解决上述技术问题，本发明所采取的技术方案是：

一种基于数据驱动的余热锅炉阀门自适应调节方法，包括下述步骤：

s1：针对余热锅炉存在多个阀门，通过数据分析以及阀门相关性研究，提出基于数据驱动的余热锅炉阀门自适应调节方法，该方法分为两个子模型，冷风阀odtva调节预测模型和入口阀&旁通阀lswbva调节预测模型；

s2：通过数据预处理，建立阀门调节与温度、压力等特征的关联性；

s3：针对冷风阀调节数据不平衡以及调节多样性的问题，构建基于过采样决策树的冷风阀odtva调节预测模型；

s4：针对入口阀&旁通阀调节依赖取风温度的时序性特征以及强相关性问题，构建基于lstm-bp共享权值神经网络的入口阀&旁通阀lswbva调节预测模型。

进一步的，所述步骤s2中通过对数据预处理，挖掘冷风阀调节与温度压力特征的关联性，其中冷风阀预测标签化是成功预测冷风阀调节的关键因素，冷风阀预测标签化步骤如下所示：

2-1)给定阀门全开的最小值open_status_value，大于该值即认为阀门处于全开状态，给定阀门全关的最大值close_status_value，小于该值即认为阀门处于全关状态；

2-2)给定参数range_number，即除全开和全闭的状态之外的状态区间数量；

2-3)针对每一个时刻的阀门开度百分比，计算它所在的状态区间，生成状态标签；

2-4)根据下一时刻的阀门状态等级和当前时刻的阀门状态等级差值进行判断，如果下一时刻的阀门状态等级大于当前时刻的阀门状态等级，则标记为增大，如果小于，标记为减小，否则，标记为不变。

进一步的，所述步骤s3中，构建冷风阀odtva调节预测模型并预测，包括以下步骤：

3-1)利用smote算法对训练集中增大、减小的类别过采样，处理冷风阀数据不平衡问题；

3-2)信息熵：针对样本数据集d＝{x⁽¹⁾,x⁽²⁾,…,x⁽ⁿ⁾}，其标签对应y＝{y⁽¹⁾,y⁽²⁾,…,y⁽ⁿ⁾}，首先计算当前样本集合d中的信息熵；

样本集合d信息熵：

其中，m代表阀门类别集合的个数，pi表示第i类别在集合d中的占比。

3-3)将连续值分割点集合tsplit。针对温度或者压力等特征是连续值的特征的情况，首先对基于该特征的数据集合进行排序，其次对相邻连续两个特征值进行求均值t，最后得到划分点集合tsplit＝[t(1),t(1),…,t(n-1)],对连续特征离散化；

3-4)信息增益：决策树在计算大量数据时，计算连续特征的信息增益时间复杂度较大，因此改进了此处的计算方式。针对锅炉特征取值上下界范围较小，而样本较多的情况，将给定一个较小的参数step,以max(1,(n*step))为步长，间隔从tsplit集合中取划分点，求解基于当前划分点划分集合产生的信息增益，最终求得该划分点集合中最大信息增益的划分点；

特征a划分集合的信息熵：

其中，v表示根据特征a将集合d划分为v个子集合，|dj|表示该子集合中的样本数。

特征a划分信息增益：

gain(a)＝info(d)-infoa(d)

其中，info(d)代表集合d的信息熵，infoa(d)表示根据特征a划分集合的信息熵。

3-5)最大信息增益。依次遍历当前特征集合中所有的特征，计算信息增益最大的特征。根据当前特征进行划分[d1,d2,…,dv]子集合，并将此特征从特征集合中移除。

3-6)构建子树。分别对[d1,d2,…,dv]子集合进行递归，重复上述步骤3-2～3-5，生成决策子树；

3-7)预剪枝。针对决策树过拟合和数据集中存在噪声等问题，采用了预剪枝的方法。当某一子集合所有的样本属于同一类时；当样本集合中样本数小于最小节点数n×threshold时；当决策树深度大于等于最大深度max_depth时，则将此集合标记为叶节点，此叶节点的类别为当前集合中样本数最多的类别。

进一步的，所述步骤s4中，构建入口阀&旁通阀lswbva调节预测模型，对入口阀、旁通阀调节预测，具体步骤如下：

针对入口阀、旁通阀调节依赖取风温度时序性特征，当取风温度异常骤升时，调节入口阀、旁通阀。如图4所示，首先通过lstm取风温度异常检测算法，利用历史取风温度预测当前取风温度，计算均值偏差判断取风温度是否异常，具体步骤如下：

4-1)输入特征。利用lstm滑动窗口方式，选择历史取风温度特征[x⁽¹⁾,x⁽²⁾,…,x^(l)]为输入特征，其中,l为取风温度历史步长的大小；

4-2)lstm预测。通过lstm算法预测最近时刻取风温度[x^(l+1),x^(l+2),…,x^(l+r)],其中r是取风温度当前时间步长的大小；

4-3)计算均值偏差。计算真实温度均值与预测温度均值的均值偏差θ，如果θ值大于阈值δ，则认为当前温度异常，需要对入口阀和旁通阀进行调节；否则为正常，当前入口阀和旁通阀状态不变；

其中x⁽ⁱ⁾表示第i时刻的真实取风温度，x⁽ⁱ⁾为第i时刻的预测取风温度，其中l表示历史步长，r表示当前时间步长。

针对入口阀、旁通阀强相关性，同时调节的问题。如图5所示，构建bp共享权值神经网络的入口阀旁通阀预测算法，通过联合损失函数loss，解决了入口阀旁通阀之间调节的强相关性问题，具体为：

其中，ki表示第i阀门的类别数，表示第i阀门真实值为j类别的概率表示第i阀门预测值为j类别的概率。

如图1所示，lswbva调节预测模型预测流程为，当入口阀全开时，利用lstm取风温度异常检测算法通过历史取风温度变化对当前一段时间段内取风温度预测，如果真实取风温度均值与预测取风温度均值差值大于偏差阈值，则通过bp共享权值神经网络算法同时对入口阀、旁通阀预测，调节入口阀旁通阀开度；小于偏差阈值则保持入口阀、旁通阀状态不变。当入口阀不是处于全开时，则直接调节入口阀、旁通阀。

采用上述技术方案所产生的有益效果在于：

针对当前余热发电系统中余热锅炉阀门往往由人工进行调节，存在调节不及时、经验不稳定等问题，本发明提出一种基于数据驱动的余热锅炉阀门自适应调节方法。该方法中冷风阀odtva调节预测模型解决了冷风阀调节时存在数据失衡以及调节多样性的问题；入口阀&旁通阀lswbva调节预测模型解决了入口阀和旁通阀调节时序性特征依赖问题，并同时精准调节入口阀和旁通阀。冷风阀odtva调节预测模型和入口阀&旁通阀lswbva调节预测模型相互配合，可以有效地完成生产状态下余热锅炉的阀门调节。

本发明中基于冷风阀odtva调节预测模型和其他模型相比：(1)可以有效地预测冷风阀状态变化；(2)由于决策树对噪声数据不敏感，针对人工调节时产生的噪声数据，odtva调节预测模型具有更好的鲁棒性，对于一些错误调节数据具有很好的修正效果；(3)该模型在阀门调节时的稳定性上具有更好的表现。

本发明中入口阀&旁通阀lswbva调节预测模型和其他模型相比：(1)可以有效地预测入口阀和旁通阀调节时机，既保证了最大程度地回收余热，又可以及时地调节入口阀和旁通阀，防止造成安全隐患；(2)有效地同时调节入口阀和旁通阀，符合实际调节情况。

将本发明提出的方法应用于某水泥生产数据上进行仿真实验，验证了提出的数据驱动的余热锅炉阀门自适应调节方法的有效性。通过对比冷风阀odtva调节预测模型与其他模型的仿真实验结果，冷风阀odtva调节预测模型在阀门状态平均绝对误差(meanabsoluteerror，简称mae)，以及阀门调节标签受试者工作特征曲线下方的面积大小(areaundercurve,简称auc)等评价指标上均优于其他模型，入口阀&旁通阀lswbva调节预测模型可有效调节入口阀及旁通阀，且可解决时间关联性问题。

附图说明

图1是基于数据驱动的余热锅炉阀门自适应调节方法架构图；

图2是冷风阀odtva调节预测模型构建流程图；

图3是入口阀&旁通阀lswbva调节预测模型预测流程图；

图4是基于lstm取风温度异常算法检测流程图；

图5是基于bp共享权值神经网络入口阀旁通阀调节预测算法流程图；

图6是冷风阀调节折线图；

图7是冷风阀调节直方图；

图8是入口阀调节折线图；

图9是入口阀调节直方图；

图10是旁通阀调节折线图；

图11是旁通阀调节直方图；

图12是冷风阀odtva调节预测模型实验仿真结果图；

图13是冷风阀smote-bp调节预测模型实验仿真结果图；

图14是冷风阀lstm调节预测模型实验仿真结果图；

图15是冷风阀smote-svm调节预测模型实验仿真结果图；

图16是lstm取风温度异常算法预测实验仿真结果图；

图17是取风温度折线图；

图18是入口阀&旁通阀lswbva调节预测模型入口阀预测实验仿真；

图19是入口阀&旁通阀lswbva调节预测模型旁通阀预测实验仿真；

图20是入口阀&旁通阀bp调节预测模型入口阀预测实验仿真；

图21是入口阀&旁通阀bp调节预测模型旁通阀预测实验仿真。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细的说明。

本发明以水泥余热发电系统中余热锅炉阀门调节为载体，通过基于数据驱动的余热锅炉阀门自适应调节方法对余热锅炉阀门进行调节，其流程图如图1所示。该方法包括下述步骤：

s1：针对余热锅炉存在多个阀门，通过数据分析以及阀门相关系数研究，提出基于数据驱动的余热锅炉阀门自适应调节方法。该方法分为两个子模型，即调节冷风阀的odtva调节预测模型和调节入口阀&旁通阀的lswbva调节预测模型。

相关系数r公式如下：

其中，xi表示第i个样本中x阀门的状态，表示x阀门样本状态均值，yi表示第i个样本中y阀门的状态，表示y阀门样本状态均值。

表1阀门相关系数

锅炉阀门调节相关性如表1所示，由相关系数可知,入口阀旁通阀调节存在强线性相关，冷风阀和其它两个阀门极低相关。由于各个阀门作用不同，单个调节预测模型无法完成对所有阀门状态预测，需要多个模型对阀门进行调节。

s2：通过数据预处理，建立阀门调节与温度、压力等特征的关联性；

针对阀门调节依赖最近时刻的阀门状态以及温度变化等特征，而决策树无法学习倒时序性特征。因此在原始特征的基础上新增了阀门调节的关键特征，保留了阀门调节数据部分时序性特征。

人工调节时会根据上一时刻的阀门状态，在上一时刻的阀门状态基础进行调节。例如：阀门处于全开或者全关闭状态时，则无法再进行增大或者减小。因此新增了上一时刻阀门状态特征。

取风温度作为余热锅炉的唯一热源，其温度的上升以及下降对锅炉内部温度具有关键性的影响。主蒸汽温度作为余热锅炉阀门调节优劣的评价指标，主蒸汽温度的上升或者下降也是阀门调节的重要依据。因此添加了取风温差以及主蒸汽温差保留了最近时刻温度变化的时序性状态。

过低的主蒸汽温度会造成能源利用率降低，而过高的主蒸汽温度会导致余热锅炉存在安全隐患，因此主蒸汽温度在调节时存在最佳阈值区间。通过对主蒸汽温度数据分析，主蒸汽温度分布服从正态分布。因此通过当前主蒸汽温度减去样本均值得到新的关键特征主蒸汽均值温差，表示当前主蒸汽温度与期望温度的偏差。

综上所述，在原有特征的基础上得到了四个新的关键特征，如表2所示：

表1新增特征

以上所有特征和原始特征合并后是冷风阀预测中的输入特征。

通过对冷风阀数据的实验和分析，工人往往是根据当前锅炉内部的温度压力特征对冷风阀状态增大、不变或减小。温度压力特征区间和当前冷风阀的状态没有明显的映射关系。因此不能直接预测冷风阀状态,需要对数据预处理，将预测类别转换为增大、不变或减小。冷风阀预测标签化是该模型成功预测冷风阀状态的关键因素。冷风阀状态标签化步骤如下所示：

2-1)给定阀门全开的最小值open_status_value,大于该值即认为阀门处于全开状态，给定阀门全关的最大值close_status_value，小于该值即认为阀门处于全关状态；

2-2)给定参数range_number,即除全开和全闭的状态之外的状态区间数量；

2-3)针对每一个时刻的阀门开度百分比，计算它所在的状态区间，生成状态标签；

2-4)根据下一时刻的阀门状态等级和当前时刻的阀门状态等级差值进行判断，如果下一时刻的阀门状态等级大于当前时刻的阀门状态等级，则标记为增大，如果小于，标记为减小，否则，标记为不变。

s3：如图2所示，针对冷风阀调节数据失衡以及调节多样性的问题，构建冷风阀odtva调节预测模型；

实际调节中，当锅炉内部温度压力处于最优阈值区间时，冷风阀状态会保持不变；当锅炉内部温度压力过高时，冷风阀处于长时间全开且保持不变；当锅炉内部温度压力过低时，冷风阀处于长时间全关且保持不变；以上三种情况导致数据集中不变类别的数据量远远多于减小和增大的类别。由于数据集类别比例失衡会对模型的预测结果造成比较大的影响，因此将采用smote过采样的方法增加少数类别数据量，提升调节预测模型的预测能力。冷风阀odtva调节预测模型如下所示：

3-1)利用smote算法对训练集中增大、减小的类别过采样，处理冷风阀数据不平衡问题；

3-2)信息熵。针对样本数据集d＝{x⁽¹⁾,x⁽²⁾,…,x⁽ⁿ⁾}，其标签对应y＝{y⁽¹⁾,y⁽²⁾,…,y⁽ⁿ⁾}，首先计算当前样本集d中的信息熵；

样本集合d信息熵：

其中，m代表阀门类别集合的个数，pi表示第i类别在集合d中的占比。

3-3)将连续值分割点集合tsplit，针对温度或者压力等特征是连续值的特征的情况，首先对基于该特征的数据集合进行排序，其次对相邻两个特征值进行求均值t，最后得到划分点集合tsplit＝[t(1),t(1),…,t(n-1)],对连续特征离散化；

3-4)信息增益。决策树在计算大量数据时，计算连续特征的信息增益时间复杂度较大，因此改进了此处的计算方式。针对锅炉特征取值上下界范围较小，而样本较多的情况，将给定一个较小的参数step,以max(1,(n*step))为步长，间隔从tsplit集合中取划分点，求解基于当前划分点划分集合产生的信息增益，最终求得该划分点集合中最大信息增益的划分点；

特征a划分集合的信息熵：

其中，v表示根据特征a将集合d划分为v个子集合，|dj|表示该子集合中的样本数。

特征a划分信息增益：

gain(a)＝info(d)-infoa(d)

其中，info(d)代表集合d的信息熵，infoa(d)表示根据特征a划分集合的信息熵。

3-5)最大信息增益。依次遍历当前特征集合中所有的特征，计算信息增益最大的特征。根据当前特征进行划分[d1,d2,…,dv]子集合，并将此特征从特征集合中移除。

3-6)构建子树。分别对[d1,d2,…,dv]子集合进行递归，重复上述步骤3-2～3-5，生成决策子树；

3-7)预剪枝。针对决策树过拟合和数据集中存在噪声等问题，采用了预剪枝的方法。当某一子集合所有的样本属于同一类时；当样本集合中样本数小于最小节点数n×threshold；当决策树深度大于等于最大深度max_depth时，则将此集合标记为叶节点，此叶节点的类别为当前集合中样本数最多的类别。

s4：针对入口阀&旁通阀调节依赖取风温度的时序性特征以及强相关性问题，构建入口阀&旁通阀lswbva调节预测模型。

针对入口阀、旁通阀调节依赖取风温度时序性特征，利用基于lstm取风温度异常检测算法，据当前一段时间内真实温度均值以及预测温度均值的均值偏差确定调节入口阀旁通阀的时机；

如图8，图9，图10，图11所示，入口阀旁通阀基本上处于稳定状态。通过数据分析得出，当取风温度特征处于正常波动时，入口阀旁通阀处于稳定不变状态。只有在取风温度特征骤升时，引起锅炉内部温度压力过高，才会减小入口阀和增大旁通阀，减少进入锅炉内部的热量。因此入口阀旁通阀的调节依赖取风温度特征的时序性变化。入口阀旁通阀调节预测模型需要可以监测到取风温度骤升的时刻，再对入口阀和旁通阀同时调节。

由于取风温度存在时序性以及较少时刻存在温度骤升情况，存在数据失衡问题。因此提出了基于lstm取风温度异常检测算法。主要思想是利用正常温度波动较多的情况检测异常温度波动较少的情况。由于大多时刻取风温度处于正常波动状态，因此在温度骤升时会出现预测偏差较大的情况，通过对偏差阈值的控制可以有效的捕获取风温度的异常状态，具体预测步骤如下所示：

4-1)输入特征。利用lstm滑动窗口方式，选择历史取风温度特征[x⁽¹⁾,x⁽²⁾,…,x^(l)]为输入特征，其中,l为取风温度历史步长的大小；

4-2)lstm预测。通过lstm算法预测最近时刻取风温度[x^(l+1),x^(l+2),…,x^(l+r)],其中r是取风温度当前时间步长的大小；

4-3)计算偏差。计算真实温度均值与预测温度均值的均值偏差θ,如果θ值大于阈值δ，则认为当前取风温度异常；

其中x⁽ⁱ⁾表示第i时刻的真实取风温度，x⁽ⁱ⁾为第i时刻的预测取风温度，其中l表示历史步差，r表示当前时间步长。

由表1阀门相关系数r可知，入口阀旁通阀具有强相关性，因此提出了基于bp的共享权值神经网络的入口阀旁通阀调节预测算法，解决入口阀旁通阀需要一起调节的问题。该算法通过联合损失函数loss，解决入口阀旁通阀之间调节的强相关性问题。该损失函数如下所示：

其中，ki表示第i阀门的类别数，表示第i阀门真实值为j类别的概率表示第i阀门预测值为j类别的概率。

通过该损失函数，可以有效的学习到冷风阀和旁通阀调节时的相关关系，以及阀门调节和温度压力特征之间的相关关系。

如图1所示，lswbva调节预测模型预测流程为，当入口阀全开时，利用lstm取风温度异常检测算法通过历史取风温度变化对当前一段时间段内取风温度预测，如果真实取风温度均值与预测取风温度均值差值大于偏差阈值，则通过bp共享权值神经网络算法同时对入口阀、旁通阀预测，调节入口阀旁通阀开度。小于偏差阈值则保持入口阀、旁通阀状态不变。当入口阀不是处于全开时，则直接调节入口阀、旁通阀。

基于上述步骤，本发明有效解决余热锅炉多个阀门的调节问题，首先，通过数据分析以及阀门相关性研究，构建基于数据驱动的余热锅炉阀门自适应调节方法。该方法分为以下分为两个子模型：针对冷风阀的调节特性，通过数据预处理，挖掘阀门调节锅炉特征的联系，构建了冷风阀odtva调节预测模型。其次，针对入口阀和旁通阀调节两者调节依赖时序性特征，且强相关性等问题，构建了入口阀&旁通阀lswbva调节预测模型。

本发明基于数据驱动的余热锅炉阀门自适应调节方法试验验证：

1、数据描述

本发明中所使用的数据来源于某水泥厂余热发电系统的实际生产中熟练工人的调节数据，传感器采集数据为5秒钟一次，为了增加样本数据的多样性，间隔1分钟取一个样本。本次研究的数据集时间为2019-4-9至2019-11-13，共计220,201个样本。

部分输入特征参数如表3所示：

表3部分特征参数

2、冷风阀odtva调节预测模型构建实验

为了验证本发明提出的冷风阀odtva调节预测模型的有效性，分别对比了该模型和与其他算法模型的性能表现，由于数据存在不平衡的问题，将通过对比各个算法的auc值作为该模型性能的评价指标。

表4odtva调节预测模型参数设置

表5决策树调节预测模型的单天数据预测

表6odtva调节预测模型单天数据预测

表7混淆矩阵

由表5，表6可以看出决策树和odtva调节预测模型在一天的数据集中auc可以达到0.9以上，证明了决策树算法在冷风阀操作分类中的有效性，odtva调节预测模型相比决策树调节预测模型，auc有显著提升，如表7所示，从混淆矩阵中可以看出odtva调节预测模型可以提高少数类别的分类准确率，从而有效的提高模型的auc值。余热锅炉阀门调节虽然不变的情况比较多，但是阀门调节的时候改变的类别更重要，因此加入smote算法可以使预测模型效果更好，更加符合实际情况。

表8odtva调节预测模型单周数据预测

如表8所示，当数据量增大时，树的深度越深，auc值会更低，出现了过拟合现象，因此数据量较大时树的深度不应该过深。

表9各调节预测模型阀门标签auc对比

如表9所示，使用单天数据量对模型训练时，odtva调节预测模型的auc最高为0.9624，远远高于其他的预测方法。通过对实验结果分析，决策树算法在生成预测标签时会少数服从多数，因此对噪声有更好的鲁棒性，针对人工调节存在一定的滞后性问题，有良好的修正效果，更适合应用于阀门调节中。

使用单周数据量对模型训练时，各个模型的auc基本均出现了下降的情况。出现这种情况是由于随着时间的增长，出现滞后性调节的情况会增多。并且由于时间较长时通常是多个工人操作单台锅炉，导致调节方式的不同而产生噪音数据。使用smote对训练集过采样后可以看出各调节预测模型的auc值均出现了提升，证明了smote算法在冷风阀门调节的有效性。通过对比各个算法，odtva调节预测模型在冷风阀操作分类实验中在一天的数据集以及一周的数据集中auc均是最高。因此odtva调节预测模型在冷风阀操作分类中效果最好。

3、冷风阀调节仿真实验

由于该模型需要应用于实际生产中，本发明根据实际的生产情况调节设计了仿真实验。使用基于单周实验训练出来的模型对单天实际生产数据的冷风阀预测调节。并通过比较各个模型的阀门预测状态与实际真实状态的mae和auc对比各个模型实际的仿真性能。由表9可知，smote算法可以显著提高各个模型的auc，因此本次仿真主要对比冷风阀odtva调节预测模型与其他过采样调节模型以及lstm调节模型的表现。

仿真调节实验的流程步骤如下：

s1：取模型所需要的数据x，使用模型预测出当前阀门操作的y，即增大，不变，减小操作。

s2：如果输出的y为增大或者减小，将当前阀门状态增加或者减小1到2个状态等级输出。如果输出状态大于阀门最大状态，将该状态设置为阀门最大状态，如果小于阀门最小状态，将该状态设置为阀门最小状态，并将下一时刻输入的数据中冷阀门状态替换成该状态。

s3：重复以上两个步骤，预测仿真集中每一时刻的阀门状态。

表10各调节预测模型仿真实验mae和auc对比

如表10所示，阀门状态mae表示阀门真实状态与预测状态偏差值，mae越小，表示当前预测状态和真实状态越接近。标签auc表示阀门预测操作的准确性，auc越高，表示对余热锅炉阀门操作越准确。从表中可以看出，odtva调节预测模型在仿真实验中具有更低的mae以及更高的auc，说明odtva调节预测模型仿真效果最好。

如图12,13,14,15所示，依次为odtva，smote-bp，lstm，smote-svm调节预测模型的仿真结果。其中，实线为真实值，虚线为预测值。可以看出smote-svm调节预测模型效果最差，由于阀门调节时在各个状态时也存在数据失衡问题，虽然对最终类别进行了过采样，在某些阀门状态时依旧存在数据失衡的问题。因此svm调节预测模型在某些阀门状态依旧偏向不变操作，使最终的拟合接近一条直线。lstm调节预测模型虽然在某些波动剧烈的时候依旧可以正常预测，但是无法提前对数据过采样，导致预测类别存在失衡问题，因此模型在实际预测中更偏向于不变的状态。从图中来看可以看出odtva和smote-bp调节预测模型在实际预测中表现较好，与smote-bp调节预测模型相比，odtva调节预测模型auc更高，表示odtva调节预测模型调节更加精准。从图中也可以看出smote-bp调节预测模型实际仿真中波动更加剧烈，稳定性比较弱，odtva调节预测模型则具有更好的稳定性。实际生产中阀门调节稳定性越高越好，因此odtva调节预测模型也更加符合实际情况。其次，odtva调节预测模型的mae比smote-bp调节预测模型更低，从图中也可以看出odtva调节预测模型相比smote-bp调节预测模型具有更好的拟合效果。通过各个调节预测模型的对比，证明了odtva调节预测模型在实际调节中的有效性。

4、基于lstm取风温度异常检测算法

表11lstm取风温度异常检测算法参数设置

如表11所示，输入层单元个数代表选用的历史步长，输出层代表选用的当前步长，为了防止过拟合，在训练时加入了dropout防止过拟合。以下是各个参数下的算法表现：

表12lstm取风温度异常检测算法各参数结果对比

通过以上实验对比，lstm滑动窗口历史步长l为10，当前步长r为3时，valloss最低，但是历史步长l为20，当前步长r为5时，测试集的均值mae最低，表示通过前20分钟预测后5分钟时，误差最小，由于该算法主要通过比较均值误差来判断当前锅炉取风温度是否异常，因此测试集的均值mae加关键。所以将选用历史步长为20，当前步长为5的参数的构建入口阀&旁通阀lswbva调节预测模型。

5、基于bp共享权值神经网络的入口阀旁通阀调节预测算法

表13bp共享权值神经网络的入口阀旁通阀调节预测算法参数设置

如表13所示，根据实际情况，本发明将使用bp神经网络直接对入口阀旁通阀状态输出，每个阀门状态为11个等级。

表14基于bp共享权值神经网络的入口阀旁通阀调节预测实验

由于入口阀旁通阀调节样本较少，类别没有失衡问题，因此这里直接对比了各个参数下算法的准确率对算法的性能进行评估，并通过最终的仿真实验验证算法有效性。如表14所示，使用bp共享权值神经网络对入口阀和旁通阀状态预测，平均准确率为83.95％，说明bp共享权值神经网络可以有效的预测入口阀和旁通阀状态。

6、基于lstm取风温度异常检测算法仿真实验

为了验证lstm取风温异常检测算法可以有效的检测温度的异常上升，使用训练好的算法对取风温度仿真预测，预测结果如下所图16所示，其中，实线为真实均值，虚线为预测均值。图17为真实取风温度波动，基于lstm神经网络的滑动窗口预测通过前一段时间对未来一段时间预测效果基本吻合真实状态下的温度均值，但是在温度骤增时会出现真实值与预测值偏差过大的问题。取风温度真实值的均值远远大于预测值的均值。在此处由于出现了温度骤升的情况，工人关小了入口阀，开大了旁通阀。因此通过设置合适的偏差阈值，计算真实均值与预测均值偏差程度，如果大于给定的偏差阈值，即认为需要调节入口阀，旁通阀。基于上述算法可以有效的预测调节入口阀和旁通阀的准确时机，能够最大限度的利用余热能源，更加符合实际的生产需要。

7、入口阀&旁通阀lswbva调节预测模型仿真实验

为了验证lswbva调节预测模型在实际中对入口阀和旁通阀的效果，通过使用训练好的lswbva调节预测模型仿真调节，验证该模型可以有效的学习到取风温度特征时间上的关联性以及阀门调节的可用性。仿真结果如图18,19,20,21所示，分别是lswbva调节预测模型和bp调节预测模型的入口阀旁通阀仿真，其中黑色实线为真实值，黑色虚线为预测值。由于bp入口阀旁通阀调节预测模型无法学习取风温度时序性特征，只能根据当前锅炉内部的温度特征对阀门进行调节，无法判断当前温度曲线变化是否需要调节入口阀和旁通阀，因此在取风温度波动稳定时，也调节了入口阀旁通阀。但是温度波动稳定时一般通过调节冷风阀控制锅炉内部温度，只有在温度骤升时才需要调节入口阀和旁通阀来控制进入锅炉内部的热量。lswbva调节预测模型可以通过学习取风温度的时序性，对锅炉取风温度异常检测，只有在锅炉温度骤升时才会调节入口阀和旁通阀，温度稳定时保持不变，因此lswbva调节预测模型相较于直接使用bp调节预测模型进行预测时，更加符合实际生产情况，能够提高能源利用率。

8、结论

本发明针对余热锅炉阀门调节问题，提出了数据驱动的余热锅炉阀门自适应调节方法，有效地将阀门调节数据转换为实际的调节预测模型。首先，通过对原始数据预处理，挖掘出了阀门调节和锅炉温度压力内部特征的关系。其次，在此基础上提出了冷风阀odtva调节预测模型。并且通过训练好的模型对实际生产阀门调节仿真实验，证明了该模型相比其他模型预测具有更好的阀门状态拟合效果mae和阀门状态调节预测auc。最后，利用lstm取风温度异常检测算法对取风温度特征状态监测，再通过bp共享权值神经网络对入口阀旁通阀调节。仿真实验结果表明，入口阀&旁通阀lswbva调节预测模型可有效的监测取风温度骤升异常情况，完成对入口阀和旁通阀精准调节，相比单独对入口阀旁通阀调节，更加符合实际的实际调节操作，可以有效提高能源利用率。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除