平动点轨道最优小推力转移分段设计方法与流程
 2021-02-15 10:02:06|
2021-02-15 10:02:06| 427|
427| 起点商标网
起点商标网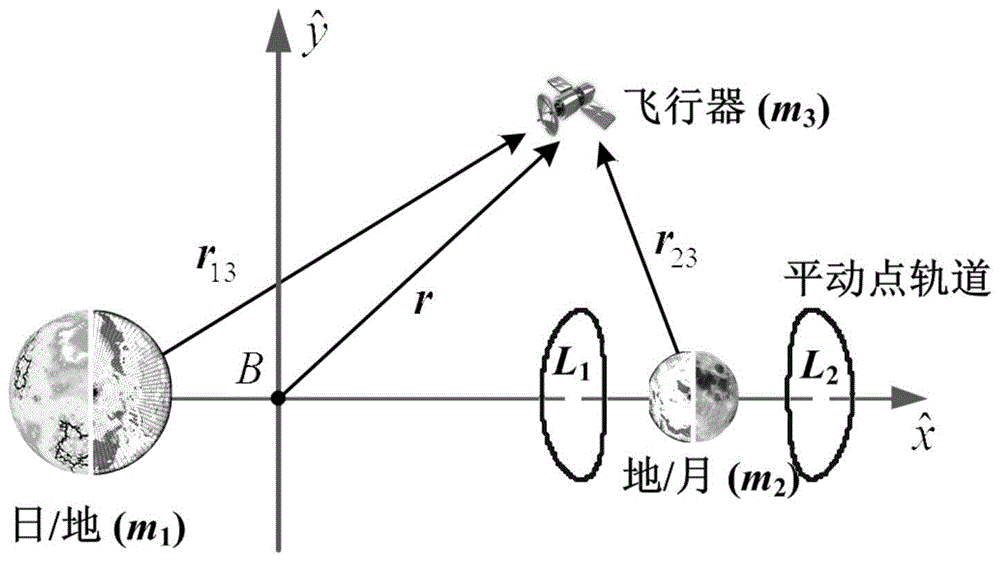
本发明涉及一种平动点轨道最优小推力转移分段设计方法。
背景技术:
平动点是限制性三体动力学中引力与惯性力相互平衡的空间点,在地球附近存在7个平动点:日地系统的l1与l2点,地月系统的l1-l5平动点。平动点附近周期轨道是空间环境观测的最佳落脚点,还可以作为未来月球探测人员与物资运输、载人火星与小行星探测任务的中转站。同时,平动点轨道任务往往存在低耗能转移轨道,探测器基于此类型轨道开展探测任务或者拓展性任务,能够有效地提升应用价值。
平动点轨道空间转移轨道设计主要分为脉冲控制与小推力控制。脉冲控制转移方式包含直接转移、弱稳定转移与借力转移。zeng采用分层微分修正策略与初值多项式,较好地解决了halo脉冲转移轨道设计中存在的多约束与初值敏感问题(zenghao,zhangjingrui.qirui,limingtao.studyoftime-freetransfersintolibrationpointorbitswithmultipleconstraints[j].journalofguidance,control,anddynamics.2017,40(11):2752-2770)。parker通过连接地月系统与日地系统空间不变流形,研究了飞行器飞抵地月l2点halo轨道的弱稳定边界转移,但存在飞行时间长等问题(parkerjs.familiesoflow-energylunarhalotransfers[c].aas/aiaaspaceflightdynamicsconference,2016)。folta提出了改进的月球引力辅助三脉冲转移方案,给出了月球借力方位与入轨点选择策略并定量分析借力约束集合的影响(foltadc,pavlakta,haapalaaf,etal.preliminarydesignconsiderationsforaccessandoperationsinearth-moonl1/l2orbit[c].aas/aiaaspaceflightmechanicsmeeting,kauai,2013)。
近些年部分学者探索了先进小推力技术与平动点任务相结合的轨道设计方法。ozimek针对平动点轨道变比冲小推力转移优化问题,推导了插入流形的一阶最优条件,但设计时未对推力和比冲设定上下限(ozimekm.low-thrusttrajectorydesignandoptimizationoflunarsouthpolecoveragemissions[d].purdueuniversity:schoolofaeronauticsandastronautics,2010)。zhang采用gauss-lobatto配点法求解了gto至地月l1和l2点lyapunov轨道的燃料最优定比冲小推力转移轨道,结合切向推力与最优控制方法降低了复杂动力学轨道设计的难度(zhangc,topputof,zazzerafb,etal.low-thrustminimum-fueloptimizationinthecircularrestrictedthree-bodyproblem[j].journalofguidance,control,anddynamics.2015,38(8):1501-2509)。
相比于脉冲平动点任务,小推力转移具有高比冲特点,能够大幅度降低任务燃料消耗,适合于对时间要求较低的空间物资运输任务,但小推力平动点任务存在多天体强引力场非线性特性,近地端多圈小推力转移计算效率低且难以收敛等问题。因此,如何快速地确定合适的拼接点,综合考虑地球停泊轨道逃逸点与流形捕获点的影响,如何有效地搜索计算可行的设计初值降低敏感性值得深入研究。
技术实现要素:
本发明的目的在于提供一种能够快速确定最优轨迹的平动点轨道最优小推力转移分段设计方法。
为实现上述发明目的,本发明提供一种平动点轨道最优小推力转移分段设计方法,包括以下步骤:
a、在质心旋转坐标系下建立飞行器的动力学方程;
b、确定平动点轨道的不变流形;
c、全局搜索确定设计变量的初值;
d、局部优化确定最优的转移轨迹。
根据本发明的一个方面,在所述步骤(a)中,所述质心旋转坐标系的原点为飞行器、第一主天体和第二主天体组成的三体系统的质心;
其中,若第一主天体为地球,则第二主天体为月球,若第一主天体为太阳,则第二主天体为地球或月球;
x轴由第一主天体指向第二主天体,z轴平行于三体系统的角动量方向,y轴由右手定则确定;
所述动力学方程包括无控动力学方程和受控动力学方程;
所述无控动力学方程为:
其中,
所述受控动力学方程为:
其中,
根据本发明的一个方面,在所述步骤(b)中,依照矩阵m的特征值与特征向量确定空间不变流形,矩阵m为:
m=φ(t0+t,t0);
其中,
则平动点轨道的不稳定流形和稳定流形在任意t时刻的线性摄动状态量分别为:
其中,上标“u”与“s”分别表示不变流形中的不稳定与稳定流形,
根据本发明的一个方面,在所述步骤(c)中,搜索方法包括:
s1、对燃料最优问题进行建模;
s2、确定并分析设计变量集合;
s3、全局搜索确定拼接点区域和设计变量的初值范围;
s4、重复步骤(s3)对拼接点区域和设计变量的初值范围进行筛选。
根据本发明的一个方面,在所述步骤(s1)中,首先确定燃料最优小推力转移轨迹,其最优性能指标maxj可表示为:
maxj=k·mf;
式中,k为任意正常数,mf为发动机关机时刻飞行器剩余质量,结合pontryagin极大值原理与所述受控动力学方程,确定系统的hamilton函数为:
则最优问题的协状态方程为:
其中,λm为协态变量。
根据本发明的一个方面,所述步骤(s2)中的设计变量集合为:
分析时将最优小推力转移轨迹分为第一小推力段、无控滑行段和第二小推力段,第一小推力段的推力方向沿速度矢量方向;
其中,
根据本发明的一个方面,在所述步骤(s3)中,基于遗传算法对设计变量进行全局搜索,确定拼接点区域和设计变量初值范围,其中优化性能指标为:
其中,||δr||和||δv||分别为第二小推力段末端与稳定流形的距离矢量与速度矢量差值,δi为末端倾角差值,系数
根据本发明的一个方面,在所述步骤(s4)中,通过重复步骤(s3)得到jga集合,并选出最小的jga,从而对拼接点区域和设计变量初值范围进行筛选,其中重复次数为10次。
根据本发明的一个方面,在所述步骤(d)中,利用局部优化算法对设计变量初值迭代求解,得到最优转移拼接点位置,其性能指标与步骤(s1)中求解最优小推力转移轨道时设定的性能指标相同,约束方程为:
式中,rs(τf,αf)与vs(τf,αf)为不变流形末端位置与速度量;r(tf2)与v(tf2)为小推力转移轨道终端位置与速度量;
进而得出约束矢量关于设计变量的偏导数关系为:
最后利用牛顿优化算法对变量ds进行迭代求解,得到满足所述约束方程的最优转移轨迹。
根据本发明的一个方案,在分析飞行器动力学方程后,对地球停泊轨道与平动点轨道的不变流形进行分析,再对近地飞行阶段小推力的推力矢量进行全局优化搜索,确定不同轨道段的拼接点位置及合适的设计变量初值。再结合局部优化算法进一步调整地球逃逸点与不变流形捕获点位置,以及转移过程推力大小与方向,能够快速且有效地设计出满足任务约束的燃料最优转移轨道。
根据本发明的一个方案,局部优化步骤中,自主搜索调整停泊轨道尺寸、初始逃逸点和目标轨道捕获点的位置及推力矢量,有效避免特征点选取不确定对燃料消耗的影响,提高设计可靠性与结果最优性。
根据本发明的一个方案,根据不同三体系统下不同平动点轨道任务要求,确定不同的小推力转移方案,能够完成相应的轨道转移设计任务,能够为未来探测器进行月球探测、空间环境观测与货物运输等任务提供参考。
附图说明
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
图1示意性表示本发明的设计方法的质心旋转坐标系的示意图;
图2示意性表示本发明的一种实施方式的设计方法的平动点轨道的稳定流形和不稳定流形示意图;
图3示意性表示本发明的一种实施方式的设计方法的转移轨道(上侧)和设计变量与策略(下侧)示意图;
图4示意性表示本发明的一种实施方式的设计方法的地月l1点晕轨道最优小推力转移轨道示意图(左为3d,右为2d);
图5是图4实施方式中的转移过程质量与推力变化曲线图;
图6示意性表示本发明的一种实施方式的设计方法的日地l1点晕轨道最优小推力转移轨道示意图(左为3d,右为2d);
图7是图6实施方式中的转移过程质量与推力变化曲线图;
图8示意性表示本发明的一种实施方式的设计方法的日地l2点晕轨道最优小推力转移轨道示意图(左为3d,右为2d);
图9是图8实施方式中的转移过程质量与推力变化曲线图。
具体实施方式
为了更清楚地说明本发明实施方式或现有技术中的技术方案,下面将对实施方式中所需要使用的附图作简单地介绍。显而易见地,下面描述中的附图仅仅是本发明的一些实施方式,对于本领域普通技术人员而言,在不付出创造性劳动的前提下,还可以根据这些附图获得其他的附图。
在针对本发明的实施方式进行描述时,术语“纵向”、“横向”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”“内”、“外”所表达的方位或位置关系是基于相关附图所示的方位或位置关系,其仅是为了便于描述本发明和简化描述,而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作,因此上述术语不能理解为对本发明的限制。
下面结合附图和具体实施方式对本发明作详细地描述,实施方式不能在此一一赘述,但本发明的实施方式并不因此限定于以下实施方式。
参见图1,本发明的一种平动点轨道最优小推力转移分段设计方法,首先在质心旋转坐标系下建立飞行器的动力学方程。质心旋转坐标系也可称为质心会合坐标系,具体如图1所示。坐标系中原点b即为三体系统的质心,三体系统由飞行器、第一主天体和第二主天体组成,其中第一、第二主天体绕质心做圆周运动。若第一主天体为地球,则第二主天体为月球,若第一主天体为太阳,则第二主天体为地球或月球。因此,三体系统也可称为地月或者日地/月三体系统,而该坐标系也可称为地球-月球(或者太阳-地球/月球)质心旋转坐标系。坐标系中,x轴由第一主天体指向第二主天体,z轴平行于三体系统的角动量方向(其垂直向外,因此在图1中无法绘出),y轴由右手定则确定。这些坐标轴的确定方法为航天领域的常识,因此不作过多介绍(坐标系中r为飞行器距离质心的距离)。飞行器的动力学方程包括了无控动力学方程和受控动力学方程(或称模型),其中受控动力学方程中引入了飞行器小推力发动机给提供的推力角速度,故此得名。在质心旋转坐标系下,飞行器(也可称航天器)的无控飞行动力学方程为:
其中,
而受控动力学方程为:
其中,
通过上述步骤,分别建立了飞行器无控和受控动力学方程,接下来要确定平动点轨道的不变流形。此步骤中,首先依据矩阵m的特征值和特征向量确定空间不变流形,其中矩阵m为:
m=φ(t0+t,t0);
其中,
则平动点轨道的不稳定流形(左式)和稳定流形(右式)在任意t时刻的线性摄动状态量分别为:
其中,上标“u”与“s”分别表示不变流形中的不稳定与稳定流形,
确定不变流形后,则可进行全局搜索(或称全局求解)设计变量的初值。在航天领域中,拼接点一般利用状态量或者坐标表示。而设计变量便可理解为能够表示拼接点的状态量。因此这一步搜索设计变量初值的同时也可确定拼接点的大致区域所在。具体的全局搜索步骤中,首先对燃料最有问题进行建模,以便求解燃料最优的小推力轨迹。在建模求解时,其最优性能指标maxj为:
maxj=k·mf;
其中,k为任意正常数,mf为发动机关机时刻飞行器剩余质量。
结合pontryagin极大值原理与上述受控动力学模方程,确定系统的hamilton函数为:
则最优问题的协状态方程为:
式中,λm为协态变量。
模型建立完成后,需确定设计变量的集合并对其进行分析求解。其中,设计变量集合为:
为了解决近地端多圈小推力求解不易收敛问题,本发明对于设计变量集合分析求解时如图3所示,将最优小推力转移轨迹分为第一小推力段a、无控滑行段d和第二小推力段b,其中第一小推力段a与地球停泊轨道c衔接。并且,第一小推力段a的推力方向沿速度矢量方向,能够有效、快速地抬高轨道高度,在短时间内降低地球强引力场的影响,提高算法的收敛性。
设计变量集合中,
τ与α分别为时间变量,其中τ用于表征平动点轨道捕获点状态量,而α表征不变流形对应时刻的状态量,用于分别求解平动点轨道与流形对应时刻的状态量,以表示拼接点流形状态量。
确定设计变量集合后,需进行全局优化搜索策略,从而能够确定拼接点的大致区域和设计变量初值的大致范围。本发明中的全局搜索主要基于遗传算法进行,其中优化性能指标为:
其中,||δr||和||δv||分别为第二小推力段b末端与稳定流形的距离矢量与速度矢量差值,δi为末端倾角差值,此判断条件能够保证小推力末端点与流形末端点的空间相对距离且速度方向相近。系数
上一步进行的全局搜索可以得到拼接点的大致区域和设计变量初值的大致范围。因此单次全局优化可能会导致搜索具有随机性,因此本发明重复进行全局搜索,以避免此缺陷。具体的,重复搜索次数在10次即可,最终能够获得上述jga的集合。基于燃料最省的原则,因此应从集合中选出最小的jga,以此来筛选出最终的拼接点区域和设计变量初值。在此需要注意,此步骤得到的最终的设计变量初值也为一个近似值,因此拼接点的区域也为一个大致区域,只是相对于单次搜索更加精确。因此,这一设计变量初值不能保证小推力轨迹与稳定流形的位置连续性,需要进行局部优化才能确定精确的拼接点位置。
具体的,本发明采用局部优化算法对设计变量初值进一步迭代求解,从而得到燃料最优转移拼接点位置。由于该拼接点位置一定位于上述最优转移轨道上,因此性能指标的设定也与上述最优小推力转移轨迹相同,而约束方程为:
式中,rs(τf,αf)与vs(τf,αf)为不变流形末端位置与速度量;r(tf2)与v(tf2)为小推力转移轨道终端位置与速度量。
通过上式可以使得小推力末端与稳定流形末端位置与速度连续,然后进而推导得出约束矢量关于设计变量的偏导数关系为:
最后利用牛顿优化算法对变量ds进行迭代求解,得到满足所述约束方程的燃料最优小推力转移轨迹。
为了验证方法的可行性,本发明针对地月l1点晕轨道(即halo轨道)最优小推力转移轨道进行设计。假设飞行器初始质量1500kg,首先选取l1点法向幅值az=10000km的halo轨道为目标轨道,结合上述设计步骤,最优小推力轨迹如图4所示,相应的质量变化与推力大小变化如图5所示。其中,平动点halo轨道、稳定流形、小推力转移轨迹(未区分第一、第二)和无控滑行轨迹分别在图中指出。分析可知:飞行器从倾角4.7°,升交点赤经15.8°与纬度幅角28.9°的geo轨道小推力发动机开机,推力大小0.6n,沿速度方向开机41.4天,开始无控滑行段飞行约2.35天,此后发动机再次开机38.72天进入稳定流形,飞行器继续沿稳定流形航行22.7天后飞抵目标halo轨道。整个过程耗时约105.1天,质量消耗约49kg。
为了验证所提设计策略的有效性,选取日地三体系统l1点与l2点halo轨道完成相应的轨道设计任务,不同工况下的小推力转移轨迹与关键参数变化如图6至图9所示。针对日地系统l1点转移任务,地球停泊轨道倾角与升交点赤经分别为7.9°与308.9°,第一小推力段a、无控滑行段d与第二小推力段b飞行时间分别为56.3天、4.1天与35.8天,飞行器进入稳定流形后继续航行约188.8天后抵达目标轨道,整个任务总飞行时间约285.01天,消耗推进剂77.05kg,小推力弧段的最大推力小于0.9n。同样的,针对l2点halo轨道任务,整个任务总飞行约310.61天,推进剂消耗约75.39kg,最大推力小于0.45n。
综上所述,本发明基于地球-月球-探测器或者太阳-地球-探测器构成的圆型限制性三体系统,结合不变流形进行全局搜索,快速确定合适的拼接点位置与设计变量初值,然后局部优化求解燃料最优小推力转移轨迹,实现探测器由地球出发至地月系统或者日地系统平动点间的转移设计。此方法能够有效地解决小推力近地多圈发散与初值猜想问题,适用范围广,能够适用于地月l1点、日地l1点与l2点的平动点轨道的转移设计。平动点轨道小推力转移策略适合于对时间无限制的空间任务,整个任务推进剂消耗较小,第一小推力段保证推力沿速度方向能够有效地提升设计策略的有效性与可行性。以上对不同三体系统不同平动点轨道的转移特性进行研究与分析,对于未来连续小推力飞行器进行地月空间物资运输及拓展性任务、策略与参数的选择等方面具有参考价值。
以上所述仅为本发明的一个实施方式而已,并不用于限制本发明,对于本领域的技术人员来说,本发明可以有各种更改和变化。凡在本发明的精神和原则之内,所作的任何修改、等同替换、改进等,均应包含在本发明的保护范围之内。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 


