一种基于轨控偏差力矩系数标定的小卫星轨控优化方法与流程

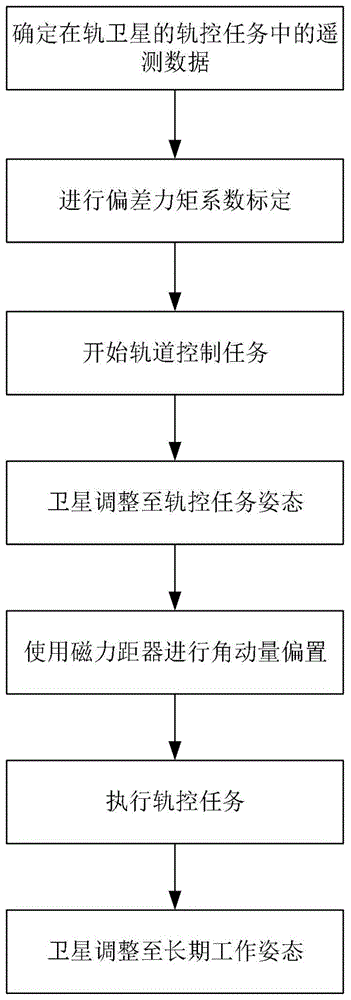
本发明属于小卫星
技术领域：
；具体涉及一种基于轨控偏差力矩系数标定的小卫星轨控优化方法。
背景技术：
：质量小于1000kg的卫星称之为小卫星，小卫星为节约研制成本，其推进系统通常只配备一个轨控推力器，由于不具备姿控推力器，因此小卫星轨道控制模式采用开环控制模式，轨道控制任务中的姿态稳定由飞轮组来保障。由于各种因素，轨控任务中推力器的推力矢量无法严格通过卫星质心，推力矢量相对于质心的偏差会形成偏差力矩。该偏差力矩在轨控任务中作用于星体，会引起整星角动量的增大，该角动量需要飞轮组进行吸收。因此，随着轨控时间的变长，偏差角动量会导致飞轮组角动量的饱和，进而对整星的姿态安全存在影响。技术实现要素：本发明提出了一种基于轨控偏差力矩系数标定的小卫星轨控优化方法，针对小卫星仅安装轨控推力器且飞轮组控制能力有限情况下轨控任务的优化方法。本发明通过以下技术方案实现：一种基于轨控偏差力矩系数标定的小卫星轨控优化方法，所述小卫星轨控优化方法包括以下步骤：步骤1：确定在轨卫星的轨控任务中的遥测数据；步骤2：根据步骤1中的遥测数据，进行轨控偏差力矩系数标定；步骤3：根据步骤2的轨控偏差力矩系数的标定结果进行轨道控制任务，卫星姿态调整至轨控任务姿态；步骤4：根据偏差力矩系数的标定结果对各轴进行角动量偏置；步骤5：执行轨道控制任务，当轨控任务完成后，调整卫星至长期工作姿态。进一步的，所述步骤2轨控偏差力矩系数标定具体包括以下两个步骤：步骤2.1：推力角度偏差，所述推力角度偏差包括推力器安装偏差角和推力轴向偏差角；步骤2.2：推力作用位置及偏差，所述推力作用位置及偏差包括卫星质心位置及偏差和推力器安装偏差。进一步的，假设卫星推力器的推力标称值为f，推力角度偏差引起的该推力在卫星本体坐标系各个轴向上的值如下：其中，[fx,fy,fz]为推力在各个轴上分量，矩阵p为推力器安装坐标系相对于卫星本体坐标系的矩阵；卫星推力器的推力矢量和推力作用位置矢量共同造成卫星的偏差力矩；由于m＝l×f，因此各个轴偏差力矩为：其中l＝[lx,ly,lz]为推力器推力作用位置在本体坐标系下坐标，m＝[mx,my,mz]为推力器在本体坐标系偏差力矩，f为推力器在本体坐标系下的推力矢量；卫星的轨控任务中半长轴变化量和推力器工作时间关系如下：其中，a为轨道半长轴，m为卫星质量，p为轨道半通径，μ为地球引力常数，e为轨道偏心率，θ为真近点角，fx和fz分别为推力在卫星x轴和z轴方向的分量，δt为推力器的工作时间；若卫星运行在圆轨道上，且轨控任务中卫星本体坐标系与卫星轨道坐标系重合，则上式简化为：由于卫星偏差力矩的积分会导致卫星角动量的变化，即卫星角动量δh＝mδt，分解到各个坐标轴如下所示：其中，δh＝[δhx,δhy,δhz]为卫星角动量的变化量；轨道控制任务引起的半长轴变化和整星角动量变化，得到下式：定义sx，sy，sz为卫星轨控任务的偏差力矩系数，如下所示：则半长轴变化和整星角动量变化的关系化简为：由式(8)可知，卫星单次轨道控制任务的半长轴控制量主要取决于，偏差力矩系数和卫星角动量变化量；其中，若偏差力矩系数为正，则轨控任务中卫星角动量正向变化，否则相反；若偏差力矩系数绝对值越大，则轨控任务中该轴角动量变化越小。进一步的，所述步骤4的调整各轴偏置角动量具体为，常规的姿态控制策略，默认会把飞轮的转速降低到较低的范围，使得整星的角动量较小。假设轨控任务的偏差力矩系数为sx,sy,sz，卫星的单轴最大吸收角动量为δhmax，且初始时刻飞轮组的各轴角动量为0，则单次轨控任务的半长轴最大控制量为：其中，smin＝min(|sx|,|sy|,|sz|)；由偏差力矩系数标定结果可知，在执行轨控任务前可以根据偏差力矩系数对各轴角动量进行提前偏置，各轴偏置量如下：偏置后单次轨控任务的半长轴最大控制量为：由式(11)可知，经角动量偏置后单次轨控任务的半长轴控制量为原来的2倍。进一步的，各轴的角动量偏置通过磁力距器进行，磁力距器偏置角动量过程如下：t＝-k(h-hn)＝-kδh(12)其中，k是控制增益，h是飞轮组的角动量矢量，hn时目标的轮组角动量矢量；δh即为需要改变的飞轮组角动量；磁力矩公式为：t＝m×b(13)则根据需要改变的飞轮组角动量δh和三轴磁强计测量得到的地球磁场强度相对于本体坐标系的矢量b，计算三个轴的磁力矩器的输出磁矩如下：本发明的有益效果是：本发明对于仅装有轨控推力器的小卫星，其轨控任务容许的最大控制量由各个轴吸收角动量的能力决定。因此，通过对推力器的偏差力矩系数进行标定，能对轨控任务前各个轴的角动量进行偏置，从而提高单次轨控任务的控制量。附图说明附图1本发明的方法流程图。具体实施方式下面将结合本发明实施例中的附图对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。实施例1一种基于轨控偏差力矩系数标定的小卫星轨控优化方法，所述小卫星轨控优化方法包括以下步骤：步骤1：确定在轨卫星的轨控任务中的遥测数据；步骤2：根据步骤1中的遥测数据，进行轨控偏差力矩系数标定；步骤3：根据步骤2的轨控偏差力矩系数的标定结果进行轨道控制任务，卫星姿态调整至轨控任务姿态；步骤4：根据偏差力矩系数的标定结果对各轴进行角动量偏置；步骤5：执行轨道控制任务，当轨控任务完成后，调整卫星至长期工作姿态。进一步的，所述步骤2轨控偏差力矩系数标定具体包括以下两个步骤：步骤2.1：推力角度偏差，所述推力角度偏差包括推力器安装偏差角和推力轴向偏差角；推力器安装偏差角为推力器轴线相对于推力器支架基准的安装偏差和推力器支架基准相对于整星基准的安装偏差的叠加；推力轴向偏差角为推力器推力方向和推力器轴线方向的夹角；其中，推力器安装偏差角为系统误差，卫星在轨期间基本不会改变。推力轴向偏差角主要取决于推力器喷口的设计精度和喷口的工质流动，属于随机误差，但该误差角度相对较小。步骤2.2：推力作用位置及偏差，所述推力作用位置及偏差包括卫星质心位置及偏差和推力器安装偏差。由卫星结构布局和卫星部件总装精度等方面的限制，推进系统的喷口方向相对质心存在位置偏差；且由于星箭分离过程中，爆炸螺栓会有一部分留在星体内；这些都会对卫星在轨实际的质心偏差产生影响；推力器安装偏差为推力器喷口相对于推力器支架基准和推力器支架基准相对于整星基准存在位置上的偏差；其中，在不考虑燃料消耗对质心的影响情况下，质心位置及偏差为系统误差，卫星在轨期间基本不会改变；推力器安装偏差为系统误差，卫星在轨期间不会改变；由上述分析可知，引起卫星轨控偏差力矩的因素主要为系统误差，在卫星推进系统工质变化较小的情况下基本不会改变；因此，轨控偏差力矩的影响因素可以进行在轨标定。进一步的，假设卫星推力器的推力标称值为f，推力角度偏差引起的该推力在卫星本体坐标系各个轴向上的值如下：其中，[fx,fy,fz]为推力在各个轴上分量，矩阵p为推力器安装坐标系相对于卫星本体坐标系的矩阵；卫星推力器的推力矢量和推力作用位置矢量共同造成卫星的偏差力矩；由于m＝l×f，因此各个轴偏差力矩为：其中l＝[lx,ly,lz]为推力器推力作用位置在本体坐标系下坐标，m＝[mx,my,mz]为推力器在本体坐标系偏差力矩，f为推力器在本体坐标系下的推力矢量；卫星的轨控任务中半长轴变化量和推力器工作时间关系如下：其中，a为轨道半长轴，m为卫星质量，p为轨道半通径，μ为地球引力常数，e为轨道偏心率，θ为真近点角，fx和fz分别为推力在卫星x轴和z轴方向的分量，δt为推力器的工作时间；若卫星运行在圆轨道上，且轨控任务中卫星本体坐标系与卫星轨道坐标系重合，则上式简化为：由于卫星偏差力矩的积分会导致卫星角动量的变化，即卫星角动量δh＝mδt，分解到各个坐标轴如下所示：其中，δh＝[δhx,δhy,δhz]为卫星角动量的变化量；轨道控制任务引起的半长轴变化和整星角动量变化，得到下式：定义sx，sy，sz为卫星轨控任务的偏差力矩系数，如下所示：则半长轴变化和整星角动量变化的关系化简为：对于小推力卫星，轨道控制任务中卫星的质量变化极小，m可以认为是定值；因此由式(8)可知，卫星单次轨道控制任务的半长轴控制量主要取决于，偏差力矩系数和卫星角动量变化量；其中，若偏差力矩系数为正，则轨控任务中卫星角动量正向变化，否则相反；若偏差力矩系数绝对值越大，则轨控任务中该轴角动量变化越小。进一步的，所述步骤4的调整各轴偏置角动量具体为，常规的姿态控制策略，默认会把反作用飞轮的转速降低到较低的范围，使得整星的角动量较小；在轨控任务期间，各个轴的角动量会单调的增大，直到达到最大角动量上限；假设轨控任务的偏差力矩系数为sx,sy,sz，卫星的单轴最大吸收角动量为δhmax，且初始时刻飞轮组的各轴角动量为0，则单次轨控任务的半长轴最大控制量为：其中，smin＝min(|sx|,|sy|,|sz|)；由偏差力矩系数标定结果可知，对于仅具有单个推力器卫星，其单次轨控任务的控制能力主要由各个轴吸收角动量的能力决定；且由偏差力矩系数可知，已知半长轴控制量能提前预测各个轴上角动量变化；因此，在执行轨控任务前可以根据偏差力矩系数对各轴角动量进行提前偏置，各轴偏置量如下：偏置后单次轨控任务的半长轴最大控制量为：由式(11)可知，经角动量偏置后单次轨控任务的半长轴控制量为原来的2倍。进一步的，各轴的角动量偏置通过磁力距器进行，磁力距器偏置角动量过程如下：t＝-k(h-hn)＝-kδh(12)其中，k是控制增益，h是飞轮组的角动量矢量，hn时目标的轮组角动量矢量；δh即为需要改变的飞轮组角动量；磁力矩公式为：t＝m×b(13)则根据需要改变的飞轮组角动量δh和三轴磁强计测量得到的地球磁场强度相对于本体坐标系的矢量b，计算三个轴的磁力矩器的输出磁矩如下：实施例2偏差力矩系数标定实例小卫星在进行开环轨控任务中，偏差力矩带来的角动量变化由飞轮组进行吸收。因此在轨控任务中通过飞轮的转速变化，分析偏差力矩带来的角动量变化。某型号小卫星安装有一个轨控推力器，3个飞轮分别安装在x，y，z轴上，其在轨期间进行的某次轨控过程中相关参数如下表所示：表1轨后任务中相关参数变化序号项目数值1卫星质量/kg67.72轨道半长轴/km69443飞轮角动量500mnms@6000rpm4轨控时间/s1345半长轴变化量/m352.546轨控前飞轮转速/rpm[1055,-3.6,-592]7轨控后飞轮转速/rpm[1972,-2582,-974]8飞轮转速变化/rpm[917,-2578.4,-382]9角动量变化/nms[0.0764,-0.2149,-0.0318]由推力系数标定公式可知，偏差力矩系数如下：sx＝170.42，sy＝-60.58，sz＝-409.44。因此，轨控任务中x轴的角动量变化与半长轴变化极性相同，y轴和z轴角动量变化与半长轴变化极性相反。同时，轨控任务中y轴角动量变化最大，z轴角动量变化最小。角动量偏置轨控任务实例假设轨控任务中，飞轮最大转速为rmax＝5000rpm。同时已知偏差力矩系数为sx＝170.42，sy＝-60.58，sz＝-409.44。根据偏差力矩系数进行角动量偏置，过程如下：smin＝min(|sx|,|sy|,|sz|)＝60.58对于各个轴的飞轮，其转速和角动量成正比。因此各个轴的初始转速:则轨控任务前各轴飞轮初始转速为：[-1777，5000，739]rpm，轨控任务完成后飞轮转速为[1777，-5000，-739]rpm。卫星单轴吸收最大角动量为δhmax＝0.416nm。半长轴控制量为：可见，通过角动量偏置，卫星的单次半长轴控制量提高至1364m。当前第1页1 2 3 

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除