一种重力场混合线性化方法与流程
 2021-02-13 23:02:28|
2021-02-13 23:02:28| 314|
314| 起点商标网
起点商标网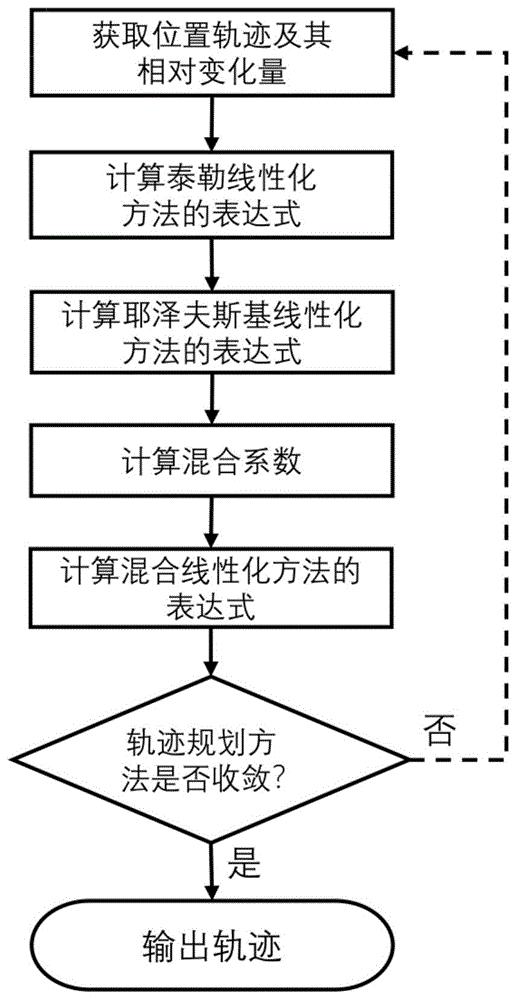
本发明涉及一种重力场的混合线性化方法,可应用于火箭动力运载器的轨迹规划方法中,属于制导、导航与控制技术领域。
背景技术:
火箭动力运载器的轨迹规划问题是一类最优控制问题。轨迹规划方法一般将轨迹规划问题转化为参数优化问题进行求解。参数优化问题的非线性程度决定其求解难度。为降低轨迹规划问题的求解难度,需要对火箭动力运载器的非线性运动方程进行线性化处理。重力场是火箭动力运载器的非线性运动方程中的主要非线性项。因此,对火箭动力运载器的轨迹进行规划时,一般需要对重力场进行线性化处理。目前,存在两种常用的线性化方法。
第一种线性化方法称为泰勒线性化方法。泰勒线性化方法采用重力场在某位置处的泰勒展开作为近似。此方法精度高,但对初始猜想非常敏感。因此,泰勒线性化方法会降低轨迹规划方法的收敛性。
第二种线性化方法称为耶泽夫斯基线性化方法。耶泽夫斯基线性化方法采用重力场在某高度处的展开作为近似。此方法对初始猜想不敏感,但精度较低。因此,耶泽夫斯基线性化方法会降低轨迹规划方法的收敛速度。
可见,应用现有的重力场线性化方法(泰勒线性化方法和耶泽夫斯基线性化方法),轨迹规划方法的收敛性或收敛速度之一会降低,不可兼得。
技术实现要素:
(一)本发明的目的
本发明的目的是提出一种重力场混合线性化方法,即一种新型的重力场线性化方法,称作混合线性化方法。此重力场的混合线性化方法可应用于火箭动力运载器的轨迹规划方法中,降低运动方程的非线性程度,从而降低求解难度。现有的线性化方法有两种:泰勒线性化方法和耶泽夫斯基线性化方法。混合线性化方法是泰勒线性化方法和耶泽夫斯基线性化方法的混合。将混合线性化方法应用至火箭动力运载器的轨迹规划方法中,能够实现两种线性化方法的优劣互补,进而同时增强轨迹规划方法的收敛性和收敛速度。收敛性和收敛速度的增强使得火箭动力运载器的轨迹规划方法的自主性和可靠性增强,在智能自主航天器的实现中具有重要价值。
(二)技术方案
本发明一种重力场混合线性化方法,可应用至火箭动力运载器的轨迹规划方法中,其具体步骤如下:
步骤一、获取位置轨迹及其相对变化量
当轨迹规划方法需要计算线性化重力场的表达式时,从轨迹规划方法中提取位置轨迹,作为重力场的线性化展开点;同时,计算位置轨迹(相对上一次迭代)的相对变化量,用于后续计算;
步骤二、计算泰勒线性化方法的表达式
应用泰勒线性化方法的公式,计算位置轨迹上重力场的表达式;
步骤三、计算耶泽夫斯基线性化方法的表达式
应用耶泽夫斯基线性化方法的公式,计算位置轨迹上重力场的表达式;
步骤四、计算混合系数
计算混合系数以混合泰勒线性化方法和耶泽夫斯基线性化方法;混合系数是一个0到1之间的数;本发明提出一个经验公式,应用位置轨迹的相对变化量以计算混合系数;
步骤五、计算混合线性化方法
应用混合系数,将泰勒线性化方法和耶泽夫斯基线性化方法混合,得到混合线性化方法的表达式,供轨迹规划方法调用。混合线性化方法的计算步骤至此结束,轨迹规划方法开始进行其他计算。当轨迹规划方法需要更新混合线性化重力场的表达式时,重新进入步骤一。
其中,在步骤二中所述的“计算泰勒线性化方法的表达式”,其具体作法如下:
从轨迹规划方法中获取位置轨迹,计算位置轨迹上的重力加速度和重力张量(即重力加速度对位置的雅可比矩阵),应用泰勒线性化方法的公式,计算得到泰勒线性化方法下重力场的表达式;
其中,在步骤三中所述的“计算耶泽夫斯基线性化方法的表达式”,其具体作法如下:
从轨迹规划方法中获取位置轨迹,应用耶泽夫斯基线性化方法的公式,计算得到耶泽夫斯基线性化方法下重力场的表达式;
其中,在步骤四中所述的“计算混合系数”,其具体作法如下:
从轨迹规划方法中获取位置轨迹及其相对变化量,应用本发明提出的经验公式计算混合系数,当相对变化量较大时,混合系数接近于1,当相对变化量较小时,混合系数接近于0。
其中,在步骤五中所述的“计算混合线性化方法”,其具体作法如下:
应用步骤四中计算的混合系数,将步骤二、三中计算的泰勒线性化方法的表达式耶泽夫斯基线性化方法的表达式进行线性加权,得到混合线性化方法下重力场的表达式。
通过以上步骤,得到了一种新型的重力场线性化方法,达到了增强火箭动力运载器的轨迹规划方法收敛性和收敛速度的作用,解决了轨迹规划方法收敛难、收敛慢的问题。
(三)本发明的优点及功效
本发明的优点及功效在于:
(1)通过混合泰勒线性化方法和耶泽夫斯基线性化方法,能够充分发挥两种线性化方法各自的优势,增强轨迹规划方法的收敛性和收敛速度;
(2)应用本发明提出的混合系数经验公式,可基于位置轨迹的相对变化量计算混合系数,使得其具有较强的通用性,能够适应不同的轨迹规划方法;
(3)本发明所述方法科学,工艺性好,具有广阔推广应用价值。
附图说明
图1是本发明的流程图。
图2是本发明提出的混合泰勒线性化方法与现有方法的对比结果一。
图3是本发明提出的混合泰勒线性化方法与现有方法的对比结果二。
具体实施方式
下面对本发明作进一步的详细说明。
火箭动力运载器的非线性运动方程为:
式中:r表示位置矢量,v表示速度矢量,g表示重力加速度矢量,t表示推力矢量,m表示火箭质量;轨迹规划方法需要将运动方程离散化为若干等式约束。非线性运动方程离散化后形成非线性等式约束,增加轨迹规划问题的求解难度。将非线性运动方程线性化后再离散化,可形成线性等式约束,求解难度相比非线性等式约束大幅降低。火箭动力运载器的非线性运动方程中,只有重力场是非线性的。因此,轨迹规划方法需要一种重力场的线性化方法。
本发明一种重力场混合线性化方法,其流程图如图1所示,包括以下几个步骤:
步骤一、获取位置轨迹及其相对变化量
从轨迹规划方法中提取位置轨迹,作为重力场的线性化展开点。同时,计算位置轨迹(相对上一次迭代)的相对变化量,用于后续计算。
位置轨迹表示为时间的函数r0,上一次迭代中的位置轨迹表示为时间的函数
步骤二、计算泰勒线性化方法的表达式
应用泰勒线性化方法的公式,计算位置轨迹上重力场的表达式;地球的非线性重力场可表达为:
式中:g表示重力加速度,μ表示地球的引力常数;
在位置轨迹r0处,泰勒线性化方法的表达式为:
式中:gt是泰勒线性化方法的表达式,
步骤三、计算耶泽夫斯基线性化方法的表达式
应用耶泽夫斯基线性化方法的公式,计算位置轨迹上重力场的表达式;
在位置轨迹r0处,耶泽夫斯基线性化方法的表达式为:
式中:gj是耶泽夫斯基线性化方法的表达式。
步骤四、计算混合系数
计算混合系数以混合泰勒线性化方法和耶泽夫斯基线性化方法;混合系数是一个0到1之间的数;混合线性化方法中,混合系数λ的确定至关重要;为增强轨迹规划方法的收敛性和收敛速度,随迭代进行,λ应从1平缓过渡至0;
本发明提出如下经验公式:
λ=(1-e-∈)3(7)
式中:∈是步骤一中计算出的相对变化量;∈远大于零时,迭代未收敛,此时λ约为1;∈接近零时,迭代接近收敛,此时λ约为0;因此,此经验公式能够实现混合系数的自动选择。
步骤五、计算混合线性化方法的表达式
应用混合系数,将泰勒线性化方法和耶泽夫斯基线性化方法混合,供轨迹规划方法调用;
混合线性化方法的表达式为:
gh(r)=(1-λ)gt(r)+λgj(r)(8)
式中:gh是混合线性化方法的表达式;
可见,混合线性化方法是泰勒线性化方法和耶泽夫斯基线性化方法的混合,而λ是混合系数;当λ=0时,混合线性化方法等价于泰勒线性化方法;当λ=1时,混合线性化方法等价于耶泽夫斯基线性化方法;当λ处于0和1之间时,重力加速度为两种线性化方法计算值的混合,因此将该方法称作混合线性化方法。
通过步骤一至五,计算出混合线性化方法的表达式,可应用至轨迹规划方法中。若轨迹规划方法的迭代未终止,则从步骤一开始,重新计算混合线性化方法的表达式进行迭代。
仿真案例:
在仿真案例中:设火箭排气速度为3400米每秒,火箭推力大小为600千牛,火箭初始质量为89吨,火箭终止质量为22吨;设初始半长轴为3600千米,初始离心率为0.81,初始轨道倾角为40度,初始升交点赤经为314.5度,初始近地点辐角为334.5度,初始真近点角为177.5度;对火箭动力运载器的轨迹规划目标是最大化终止半长轴,终止离心率为0,终止轨道倾角为42度,终止升交点赤经为313度。
仿真案例中,选择凸规划方法作为火箭动力运载器的轨迹规划方法。凸规划方法可应用各种重力场的线性化方法,包含泰勒线性化方法、耶泽夫斯基线性化方法,以及本发明提出的混合线性化方法。分别应用现有的泰勒线性化方法和耶泽夫斯基线性化方法,以及本发明提出的混合线性化方法求解仿真案例,结果如图2和图3所示。应用泰勒线性化方法求解仿真案例时,第5次迭代中发散,未能规划出轨迹。说明耶泽夫斯基线性化方法和混合泰勒线性化方法的收敛性优于泰勒线性化方法。而混合泰勒线性化方法的收敛速度优于耶泽夫斯基线性化方法,能够在较少的迭代次数内得到较高的轨迹精度。可见,在一样的轨迹规划方法(凸规划方法)中,应用不同的重力场线性化方法,轨迹规划方法的收敛性和收敛速度不同。本发明提出的混合线性化方法可同时增强轨迹规划方法的收敛性和收敛速度。
仿真案例验证了混合线性化方法能够充分发挥混合泰勒线性化方法和耶泽夫斯基线性化方法各自的优势,进而增强轨迹规划方法的收敛性和收敛速度。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 



