一种基于自主滤波阶切换的非线性卫星轨道确定方法与流程

2021-02-13 05:02:39|

393|

起点商标网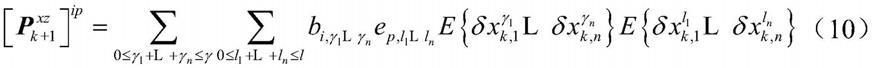

[0001]
本发明属于卫星轨道确定领域，涉及一种基于自主滤波阶切换的非线性卫星轨道确定方法。

背景技术：

[0002]
近年来，随着人类空间活动的精细化和多样化，对在轨卫星轨道确定提出了更高的要求，包括高精度和高效率，低测量需求，低初值依赖度等。然而，对于目前大多数的常规滤波器，例如卡尔曼滤波器、扩展卡尔曼滤波器、粒子滤波器等传统的滤波器等，总是无法满足所有这些要求。潜在的能够同时满足上述性能要求的滤波器只有无味卡尔曼滤波器和基于泰勒多项式展开技术的非线性扩展卡尔曼滤波器，两者在非线性较强时展现出了特别优良的性能，但是当系统的非线性过于强时，两种滤波器都将因为过于承重的计算成本而失效。然而，失效的原因却截然不同，一般来说，无味卡尔曼滤波器是因为过多的采样点导致的重复性计算而失效，而作为一种半解析方法，非线性扩展卡尔曼滤波器则是由于滤波阶过高导致用于逼近的近似多项式过于复杂。另外，无味卡尔曼滤波器只能达到二阶精度，而理论上来说非线性扩展卡尔曼滤波器可以达到任意高阶。
[0003]
另一方面，非线性扩展卡尔曼滤波器具有良好的推广性，即其低阶算法和高阶算法的算法执行过程完全相同，唯一的区别在于算法执行过程的展开阶选择。当选择滤波阶为1时，非线性扩展卡尔曼滤波器将退化为常规的扩展卡尔曼滤波器，显然，低阶算法可以获得良好的计算效率却有可能遭遇精度损失，相反，当选择滤波阶较高时，非线性扩展卡尔曼滤波器可以获得较高的精度却面临着巨大的计算压力。因此，如何克服非线性扩展卡尔曼滤波器在不同滤波阶时遭遇的问题而同时获得低级算法和高阶算法的优势，具有非常重要的实际意义。

技术实现要素：

[0004]
本发明的目的在于克服上述现有技术中，非线性扩展卡尔曼滤波器不能同时获得低级算法和高阶算法的优势的缺点，提供一种基于自主滤波阶切换的非线性卫星轨道确定方法
[0005]
为了达到上述目的，本发明采用以下技术方案予以实现：
[0006]
一种基于自主滤波阶切换的非线性卫星轨道确定方法，包括如下步骤：
[0007]
步骤一，建立方程：分别建立航天器轨道动力学方程和观测方程；
[0008]
步骤二，非线性状态和测量预测：分别对步骤一的轨道动力学方程和观测方程进行泰勒展开逼近，得到轨道状态的高阶多项式映射和观测方程的高阶多项式映射，并根据上一时刻状态统计信息计算得到状态预测值；
[0009]
步骤三，计算测量新息，并进行卡方检测，根据结果对步骤二的两个高阶多项式映射过程进行自主阶切换；当系统非线性状态较强时，自主阶切换算法采用高阶算法进行滤波；当系统非线性状态较弱或滤波过程进入稳定状态时，自主阶切换算法采用低阶算法
进行滤波；
[0010]
步骤四，状态更新：设置时间参数、初始状态和当前时刻测量值，采用步骤三选择的自主阶切换算法，对步骤二中得到的状态预测值进行更新，得到目标时刻航天器的轨道状态。
[0011]
优选地，步骤一建立的轨道动力学方程为：
[0012][0013]
式(1)中，x表示n维状态变量，t表示时间；假设t0时刻航天器的状态为x0，该常微分方程的解表示为x(t)＝φ(t；t0,x0)；
[0014]
航天器的观测方程为：
[0015]
z＝h(x,t)+u
ꢀꢀꢀ
(2)
[0016]
式(2)中，z表示t时刻的观测量，x表示t时刻的状态值，u表示t时刻的观测噪声。
[0017]
优选地，步骤二所述的非线性状态预测包括两个，分别为
[0018]
1)对轨道运动进行非线性状态预测，具体为：
[0019]
假设t
k
时刻航天器的标称状态为初始偏差为δx
k
，此时多项式形式的状态变量表示为将该多项式变量在区间[t
k
,t
k+1
]上进行积分，得到微分方程在t
k+1
时刻的解为
[0020]
对该解在标称状态处做泰勒展开，得到高阶展开式
[0021]
其中，δx
k+1
＝t
xk+1
(δx
k
)，表示状态邻域[x
k+1
]对初始邻域大小δx
k
的非线性依赖关系；
[0022]
2)对航天器的观测进行非线性预测，具体为：
[0023]
时间为t
k+1
时的测量方程为：
[0024]
z
k+1
＝h(x
k+1
,t
k+1
)+u
k+1
ꢀꢀꢀ
(3)
[0025]
其中，z
k+1
表示t
k+1
时刻的观测量，x
k+1
表示t
k+1
时刻的状态预测值，u
k+1
表示 t
k+1
时刻的观测噪声，在t
k+1
时刻，将方程(3)在标称状态处做泰勒展开，得到高阶展开式，
[0026][0027]
式(4)中，p表示m维测量矢量的索引值，表示t
k+1
时刻的标称观测矢量，系数表示泰勒展开系数，表示t
k
时刻第i个状态偏差分量，其阶数为γ
i
；γ＝[γ1,l,γ
n
]
t
，表示各状态偏差分量的阶数。
[0028]
优选地，高阶展开式的γ阶多项式的近似解表示为：
[0029][0030]
式(5)中，i表示n维状态矢量的索引值；表示标称状态； δx
k
＝[δx
k,1
，l,δx
k,n
]
t
，表示初始偏差；表示相应的泰勒展开式系数， γ＝[γ1,l,γ
n
]
t
表示各状态偏差分量的指数。
[0031]
优选地，步骤二所述的非线性状态预测过程中，轨道运动的预测状态均值和协方差矩阵为：
[0032][0033][0034]
其中，e[]表示期望值，γ＝[γ1,
…
,γ
n
]
t
和l＝[l1,
…
,l
n
]
t
表示变量偏差分量的指数，表示过程噪声的协方差矩阵；式(7)中，和其余的和与对应的均相等。
[0035]
优选地，预测观测值的均值和协方差矩阵p
k+1
如下：
[0036][0037][0038][0039]
其中p和q表示测量矢量的索引值，i表示状态的索引值，表示观测噪声的协方差矩阵；表示状态矢量和测量矢量的协态矩阵，表示测量值协方差矩阵；e[]表示期望值；式(9)中，其余的均与对应的相等。
[0040]
优选地，步骤三所述的滤波阶切换具体为：
[0041]
定义测量新息矢量v
k+1
和相应的协方差矩阵s
k+1
为
[0042][0043][0044][0045]
定义t
k+1
时刻的卡方指标归一化值为
[0046][0047]
定义t
k+1
时刻的卡方指标的时间平均值为
[0048][0049]
其中，u
k+1
表示t
k+1
时刻的观测噪声；r
k+1
表示t
k+1
时刻观测噪声的协方差矩阵， e[]
表示期望值，l表示数据采集的窗口宽度，l等于3。
[0050]
优选地，步骤三所述的自适应滤波切换的具体过程包括两种状态，分别为：
[0051]
1)滤波器需要保持滤波阶γ，此时滤波器不能正常工作，滤波器自动增加滤波阶，其中可根据m和α值查卡方值表得到；
[0052]
2)滤波器在滤波阶为γ时正常工作，此时滤波器正常工作，之后进行降低滤波阶存在的可能验证过程。
[0053]
优选地，降低滤波阶存在的可能性验证过程，包括：当滤波器将尝试降低滤波阶γ；否则将保持滤波阶不变；其中，和通过卡方分布的概率表得到。
[0054]
优选地，步骤四所述的非线性状态更新的具体过程为：
[0055]
通过观测设备得到t
k+1
时刻新的观测值时，将其融合到预测值中，得到卡尔曼滤波器的增益k
k+1
、状态的估计值和协方差矩阵
[0056][0057][0058][0059]
与现有技术相比，本发明具有以下有益效果：
[0060]
本发明公开了一种基于自主滤波阶切换的非线性卫星轨道确定方法，利用高阶方法适合于非线性较强时的精确状态估计，及低阶方法适合于滤波器进入平稳阶段的高效率滤波，通过设计自适应滤波阶切换策略，在保证精度的前提下，在一个估计过程中根据需要动态改变滤波阶。在滤波过程中，通过计算测量新息并检验滤波一致性特性，动态地设计了一个自适应自主滤波阶切换策略，当系统非线性较强时，采用高阶算法保证精度；当滤波过程进入稳定状态时，采用低阶算法保证效率。本发明提出的基于自主滤波阶切换的非线性卫星轨道确定方法是一种混合算法，同时获取了低阶算法和高阶算法的优点。确保非线性扩展卡尔曼滤波器在保证精度的前提下，加快滤波过程的执行速度。本发明提出的基于自主滤波阶切换的非线性卫星轨道确定方法，在保证精度的前提下，可以降低滤波器在滤波平稳阶段的滤波阶，显著减少计算成本，提高计算效率。克服了传统的非线性扩展卡尔曼滤波器在一个估计过程中无法改变滤波阶的困境，不仅保持原有非线性扩展卡尔曼滤波采用高阶时的高精度特点，同时继承了低阶运行时的高效率。本发明提出的基于自主滤波阶切换的非线性卫星轨道确定方法普遍适用于卫星、空间碎片等的轨道确定，可加速高精度卫星轨道确定的执行速度。
[0061]
进一步地，通过对滤波过程中测量新息的监测在保证滤波一致性的要求下，动态地调整滤波平稳阶段的滤波阶，大大降低了滤波器的计算成本，进一步优化了卫星轨道确定的执行速度。
附图说明
[0062]
图1为标准一阶、二阶非线性扩展卡尔曼滤波器和本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器得到的位置误差示意图；
[0063]
图2为标准一阶、二阶非线性扩展卡尔曼滤波器和本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器得到的速度误差示意图；
[0064]
图3为标准一阶、二阶非线性扩展卡尔曼滤波器和本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器得到的位置分量标准差估计值示意图；
[0065]
图4为标准一阶、二阶非线性扩展卡尔曼滤波器和本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器得到的速度分量标准差估计值示意图。
具体实施方式
[0066]
为了使本技术领域的人员更好地理解本发明方案，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分的实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都应当属于本发明保护的范围。
[0067]
需要说明的是，本发明的说明书和权利要求书及上述附图中的术语是用于区别类似的对象，而不必用于描述特定的顺序或先后次序。应该理解这样使用的数据在适当情况下可以互换，以便这里描述的本发明的实施例能够以除了在这里图示或描述的那些以外的顺序实施。此外，术语“包括”和“具有”以及他们的任何变形，意图在于覆盖不排他的包含，例如，包含了一系列步骤或单元的过程、方法、系统、产品或设备不必限于清楚地列出的那些步骤或单元，而是可包括没有清楚地列出的或对于这些过程、方法、产品或设备固有的其它步骤或单元。
[0068]
下面结合附图对本发明做进一步详细描述：
[0069]
实施例1：
[0070]
本实例公开一种基于多项式展开技术的高阶容错卫星轨道确定方法，具体实现步骤如下：
[0071]
步骤一：建立无量纲的卫星轨道状态方程为
[0072][0073]
其中分别表示无量纲的时间，卫星的无量纲位置矢量、速度矢量和角速度值，t，r，v，ω表示相应的有量纲值，表示卫星无量纲位置矢量的范数；另外，卫星的标称角速度表示卫星在半长轴为 a＝42164km的轨道上运行的平均的轨道角速度，μ
e
表示地球的引力常数。
[0074]
步骤二：建立非线性测量方程，包括径向距离，赤经和赤纬，
[0075][0076]
其中u＝[u1,u2,u3]
t
表示测量噪声矢量，径向距离的测量噪声满足零均值标准差为1米的高斯分布，赤经和赤纬的测量噪声满足零均值标准差为1.745
×
10-6 rad的高斯分布。同时，我们假设每个轨道可以获得12个等间距的测量值。
[0077]
步骤三：非线性状态预测：
[0078]
假设t
k
时刻航天器的标称状态为初始偏差为δx
k
，因此初值的一个邻域可表示为被称为多项式状态变量，在区间[t
k
,t
k+1
]上进行积分后得到微分方程在t
k+1
时刻的解为对该解在标称状态处做泰勒展开可得到高阶展开式其中表示状态t1状态邻域[x
k+1
] 对初始邻域大小δx
k
的非线性依赖关系，其γ阶多项式近似解可表示为
[0079][0080]
其中，i表示状态矢量的索引值，表示标称状态； δx
k
＝[δx
k,1
,l,δx
k,n
]
t
表示初始偏差，表示相应的泰勒展开式系数， γ＝[γ1,l,γ
n
]
t
表示各状态偏差分量的指数。
[0081]
进一步的，在t
k+1
时刻，使用γ阶多项式形式的解，即方程(5)，预测状态均值和协方差矩阵如下
[0082][0083][0084]
其中，e[]表示期望值，γ＝[γ1,
…
,γ
n
]
t
和l＝[l1,
…
,l
n
]
t
表示变量偏差分量的指数，表示过程噪声的协方差矩阵；方程(7)中的系数与除了和之外，与对应的均相等。
[0085]
类似的，根据测量方程(2)，t
k+1
的测量方程可表示为
[0086][0087]
其中，z
k+1
表示t
k+1
时刻的观测量，x
k+1
表示t
k+1
时刻的状态预测值，u
k+1
表示 t
k+1
时刻的观测噪声，在t
k+1
时刻，将方程(3)在标称状态处做泰勒展开可得到高阶展开式
[0088][0089]
其中p表示m维测量矢量的索引值，表示对应于标称观测
值，系数表示泰勒展开系数，可通过将方程(5)代入方程(3)计算得到， m表示观测方程的数量；在t
k+1
时刻，使用γ阶多项式形式的解，即方程(4)，预测观测值的均值如下：
[0090][0091][0092][0093]
其中p和q表示测量矢量的索引值，i表示状态的索引值，表示观测噪声的协方差矩阵，系数与除了和之外，与对应的均相等。
[0094]
步骤四：滤波阶切换策略
[0095]
定义测量新息矩阵v
k+1
和相应的协方差矩阵s
k+1
为
[0096][0097][0098][0099]
进一步，q
k+1
定义为
[0100][0101]
定义时间平均的新息平方归一化值(nis)为
[0102][0103]
其中，l表示数据采集的窗口宽度，默认为3。
[0104]
为了设计自适应的滤波阶切换策略，先提出两个假设
[0105]
1)h0：滤波器在滤波阶为γ时正常工作；
[0106]
2)h1：滤波器需要保持滤波阶γ。
[0107]
在假设h0成立时，新息平方归一化平均值是一个具有m个自由度卡方分布其中重要性系数α＝99％，因此我们可以通过卡方分布的概率表得到对应于参数m和α的临界值当时，假设h0不成立而假设h1成立，即滤波器不正常工作，滤波器自动增加滤波阶。当时，假设h1不成立而假设h0成立，即滤波器正常工作，在这种情况下，我们需要进一步验证是否存在降低滤波阶的可能性。类似的，我们提出以下两个假设：
[0108]
1)滤波器可以尝试降低滤波阶γ；
[0109]
2)滤波器在滤波阶为γ时不正常工作。
[0110]
为了验证和我们需要围绕定义一个严格的区间一般情况，α
l
＝10％，α
u
＝75％，因此我们可以通过卡方分布的概率表得到对应于参数α
l
和α
u
的临界值和当表明当前滤波器的一致性非常号，因此滤波器将尝试降低滤波阶γ，否则将保持滤波阶不变。
[0111]
步骤五：非线性状态更新
[0112]
通过观测设备得到t
k+1
时刻新的观测值时，将其融合到预测值中，可以得到卡尔曼滤波器的增益，以及状态的估计值和其协方差矩阵
[0113][0114][0115][0116]
步骤五：反复执行上述算法，得到任意时刻航天器的轨道状态。
[0117]
对本发明方法进行验证：
[0118]
地球同步轨道卫星的初始状态为
[0119][0120]
初始位置误差为100km，初始速度误差为0.01km/s。同时我们假设地球同步轨道卫星只有在晚上的12个小时可以进行观察，且每天可以均匀地获取十二个测量量。
[0121]
图1和图2展示了分别由标准一阶、二阶非线性扩展卡尔曼滤波器和本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器得到的位置和速度误差。仿真结果表明二阶非线性扩展卡尔曼滤波器和本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器具有相同的估计精度，最终的位置误差为4.9m，速度误差为0.0004m/s，相反，一阶非线性扩展卡尔曼滤波器由于在初始滤波阶段对状态误差的高估导致了精度的损失，如图3和图4所示。
[0122]
另外，表1展示了三种滤波器消耗的计算成本(cpu时间)以及滤波器在平稳阶段的速度和位置误差。
[0123]
表1：仿真得到的平均误差和cpu时长
[0124]
滤波器位置误差(千米)速度误差(米/秒)cpu时长(秒)hekf-10.19940.014624.3hekf-20.00490.000438.7ahekf0.00490.000426.1
[0125]
表1的结果表明，本发明提出的基于滤波阶切换的非线性扩展卡尔曼滤波器，在
计算效率方面只比一阶非线性扩展卡尔曼滤波器慢一点，却获得了和二阶非线性扩展卡尔曼滤波器几乎相同的估计精度。
[0126]
综上所述，为了改善现有的非线性扩展卡尔曼滤波器在低阶滤波和高阶滤波时存在的缺点，本发明通过动态地监测滤波过程中测量新息，验证滤波一致性特征，并以此为依据提出了一种自适应自主切换滤波阶的高效策略，该方法不仅保持原有非线性扩展卡尔曼滤波采用高阶时的高精度特点，同时继承了滤波器在低阶运行时的高效率特点。
[0127]
以上内容仅为说明本发明的技术思想，不能以此限定本发明的保护范围，凡是按照本发明提出的技术思想，在技术方案基础上所做的任何改动，均落入本发明权利要求书的保护范围之内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击【在线咨询】或添加微信【19522093243】与客服一对一沟通，为大家解决相关问题。