一种可倾转旋翼的复合结构飞行器的制作方法

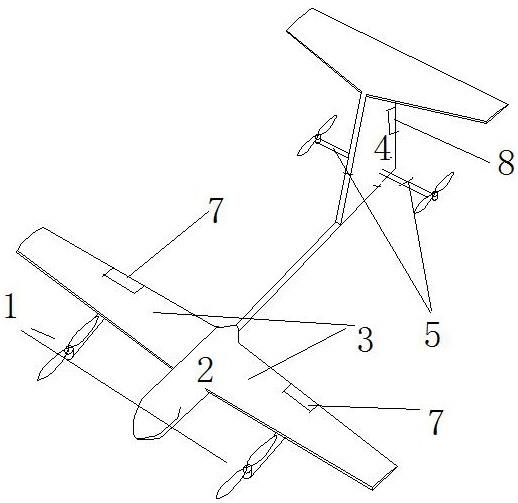
[0001]
本发明涉及飞行器技术领域，尤其是一种可倾转旋翼的复合结构飞行器。


背景技术：

[0002]
固定翼无人飞行器和旋翼无人飞行器作为传统无人飞行器结构的代表，长期以来在军事和民用领域发挥着重要作用。然而，它们的应用总是受到灵活性、有效载荷和续航时间的限制，这些都与它们自身的典型结构和动力系统有关。比如旋翼飞行器虽然具备短距起降的能力，但是续航时间较短。固定翼无人飞行器虽然具备较长的续航时间，但是使用受限于飞行场地，且灵活性较差。


技术实现要素：

[0003]
本发明提出一种可倾转旋翼的复合结构飞行器，较好地综合了固定翼飞行器和旋翼飞行器的优点，同时改进了现有的控制系统，使其具有更高的可靠性、抗干扰性和控制性能。
[0004]
本发明采用以下技术方案。
[0005]
一种可倾转旋翼的复合结构飞行器，所述飞行器的机身包括用于空中巡航的主翼和尾翼；所述主翼设于机身中段；所述尾翼设于机身尾部；飞行器还设有用于为飞行器提供动力的旋翼；所述旋翼包括设于固定翼处的第一旋翼组，还包括设于机身后部的第二旋翼组；当飞行器起飞或降落时，所述第一旋翼组、第二旋翼组内各旋翼的朝向均为竖向以向机身提供升力，当飞行器处于空中巡航状态时，所述第二旋翼组内的各旋翼朝向调整至水平方向，为飞行器提供推力。
[0006]
所述述第一旋翼组内各旋翼的朝向固定为竖向。
[0007]
所述第一旋翼组内各旋翼固定于主翼前部；第二旋翼组内各旋翼固定于尾翼根部处。
[0008]
所述主翼、尾翼的翼面均包括可变角度的翼面部位，所述主翼以可变角度的翼面部位形成升降舵；所述尾翼以可变角度的翼面部位形成方向舵；当飞行器处于空中巡航状态时，第一旋翼组内的各旋翼处于停机状态。
[0009]
所述机身尾部设有与第二旋翼组相连的连杆机构；所述连杆机构可同步调整第二旋翼组内各旋翼的朝向，使之在水平与竖向之间切换。
[0010]
第一旋翼组、第二旋翼组均由两个以小转子驱动的旋翼组成；所述飞行器为无人机，无人机的机身载有自动驾驶仪、传感组件和用于与地面站通讯的遥控组件；所述传感组件包括速度传感器、全球定位器、惯性测量单元和压力传感器；自动驾驶仪通过传感组件测量飞行器工况以优化对飞行器的控制。
[0011]
所述飞行器还包括基于线性模型的控制器；所述控制器基于鲁棒伺服线性二次调节器rslqr和扩展状态观测器eso相结合的飞行控制律来控制飞行器的飞行。
[0012]
所述飞行控制律中的动力学模型为非线性动力学模型，其以机身固定框架bff附
加到飞行器的重心位置cog来建立坐标系，方法为将惯性固定式框架eff表示为o
g
x
g
y
g
z
g
，其原点设置于起始点；建立四个辅助框架afs的坐标系o
i
x
ti
y
ti
z
ti
(i＝1,2,3,4)，基于对倾斜角度和侧倾角的考虑,z
ti
轴沿着旋翼的螺旋桨轴；x
ti
轴平行于无人机的纵向平面,垂直于z
ti
轴并垂直纸面向外；y
ti
轴由右手定则确定；不同坐标系之间以坐标转换原理设置坐标系之间的变换矩阵为：
[0013][0014]
φ、θ、ψ代表了欧拉角，c和s分别是余弦和正弦函数的符号，η是固定的侧倾角，用于推进系统以提高其可控性，ε是转子的倾斜角度；
[0015]
所述非线性动力学模型可导出为牛顿-欧拉公式，可将惯性固定式框架表示为:
[0016][0017]
其中m是飞行器质量，和分别表示惯性固定式框架中的合力矢量和合力矩矢量，v
b
＝[u,v,w]
t
是速度矢量,ω
b
＝[p,q,r]
t
为姿态角速率向量，i
b
为刚体惯性矩阵，可表示如下:
[0018][0019]
机身固定框架中表示的力f和力矩m是由重力、推进系统、空气动力和转子倾斜作用引起的陀螺效应所产生的，它们可以表示为：
[0020]
[0021]
其中所有的分力和力矩采取下面的形式表示
[0022]
惯性固定式框架中的重力可以表示为：
[0023][0024]
所述第二旋翼组为飞行器在空中巡航时的推进系统，推进系统推进矢量的表示方法为利用辅助框架与机身固定框架bff之间的旋转矩阵，可以将推力矢量沿着机身固定框架分解，得到以下公式，
[0025][0026]
其中，t
ia
为用辅助框架表示的推力矢量，t
i
为推力值，δ
i
为马达节流，g
ti
(
·
)为实验确定的数学关系；由推进系统产生的力矩矢量可以表示为：
[0027][0028]
其中为推力矢量产生的力矩矢量，d
i
是从齿轮到各转子轴的位置矢量，τ
i
表示转子空气阻力引起的力矩，表示辅助框架afs中的力矩矢量，表示机身固定框架(bff)中的力矩矢量；
[0029]
推进系统中旋翼的转子旋转会产生陀螺旋进动力矩效应。该力矩向量的表达式如下：
[0030][0031]
其中j
ri
是推进组件绕其轴线的惯性矩，ω
i
代表辅助框架(afs)中转子的旋转角速度矢量；
[0032]
当在飞行模型中引入方向舵因素时，所述飞行器的空气动力和力矩如下:
[0033][0034]
其中，q是动压，α是迎角，β是侧滑角，δ
α
、δ
e
和δ
r
分别是副翼、升降舵和方向舵的偏转角；
[0035]
设ζ＝[x,y,z]
t
表示飞机在惯性固定式框架中的位置向量，则根据坐标系之间的转换关系，平移运动方程和旋转运动方程可以表示为：
[0036][0037]
基于上述内容，飞行模型系统的6自由度非线性动力学方程可以用一阶向量微分方程的形式来描述:
[0038][0039]
其中x是状态变量u,v,w,p,q,r,φ,θ,ψ,x
g
,y
g
,z
g
的向量，u是输入变量的向量，包括马达节流δ1、δ2、δ3和δ4以及操纵面偏转δ
α
、δ
e
、δ
r
，在飞行器从空中巡航转为起降作业时的过渡模式以及飞行器空中巡航时的固定翼模式下被考虑。
[0040]
所述线性控制器基于通道节流和配平计算进行控制分配，具体包括垂直通道δ
h
、俯仰通道δ
θ
、翻滚通道δ
φ
、偏航通道δ
ψ
，
[0041]
四个通道的虚拟控制输入和推进器的实际节流之间的关系建立如下:
[0042][0043]
其中δ
hi
,δ
θi
,δ
φi
,δ
ψi
(i＝1,2,3,4)分别是垂直通道δ
h
、俯仰通道δ
θ
、翻滚通道δ
φ
、偏航通道δ
ψ
的节流阀的重量；
[0044]
当飞行器处于平衡状态时，基于公式11中的非线性动力学方程，可得到下面的扰动平衡方程:
[0045][0046]
其中δ(
·
)＝(
·
)-(
·
)
op
，“op”表示操作点；
[0047]
根据以上描述，四个通道的修整条件可以表示为:
[0048][0049]
设飞行器工作于旋翼飞行器模式时，气动效应器和陀螺效应器的效率低至可忽略不计；设飞行器工作于直升机模式时，ε、θ和φ等于零；设较小的高阶项视为可忽略，则可以得到：
[0050][0051]
其中
[0052]
设第一旋翼组内有两个旋翼，分别由第一电机、第二电机驱动，且由于第一旋翼组、第二旋翼组几何参数不对称，第一和第二电机首先达到最大容量，则可以基于第一电机获得每个通道的权重系数，计算结果如下所示:
[0053][0054]
最后，通道输入和实际节流阀之间的控制分配关系可以通过将公式17代入公式13来获得。
[0055]
当飞行器工作于旋翼飞行器模式时，若需引入状态向量以进行姿态控制和高度控制，则对公式11中的非线性动力学方程进行分割，得到和输入向量此时飞行模型系统可表述为
[0056][0057]
所述飞行模型系统在平衡操作点处被线性化，通过泰勒级数展开并在一阶项中截断。因此，线性化的飞行模型系统以如下公式所示:
[0058][0059]
其中，
[0060]
飞行器模型系统的线性化系统方程可基于公式19进一步表述为
[0061][0062]
其中y
c
是输出向量，c
c
是相应的转移矩阵；
[0063]
基于鲁棒伺服线性二次调节器rslqr的控制方法是在线性二次调节器lqr控制方法的基础上，通过在系统中引入状态偏差而得，此状态偏差可以被调整到零，使得系统状态变量可以精确地跟踪输入命令；
[0064]
如果偏差假定为e＝r
c-y
c
，其中r是控制指令，则飞行器状态方程可以定义为：
[0065][0066]
其中
[0067]
鲁棒伺服线性二次调节器rslqr控制的代价函数由下式给出：
[0068][0069]
其中q和r是权重矩阵；控制器的控制系统选择矩阵r作为单位矩阵，矩阵q作为对角矩阵；矩阵q中的值使用布赖森bryson定律进行缩放；最后，鲁棒伺服线性二次调节器rslqr控制的增益矩阵可以表示为:
[0070]
k
c
＝[k
i
,k
p
]＝r-1
b
t
p
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(公式23)
[0071]
其中k
i
、k
p
是不同的分块矩阵，它们具有相同的维度e和p(＝p
t
＞0)是下列代数黎卡提方程的解:
[0072]
pa+a
t
p-pbr-1
b
t
p+q＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(公式24)
[0073]
鲁棒伺服线性二次调节器rslqr控制的最佳控制输入如下述公式25所示，
[0074][0075]
所述rslqr控制在状态反馈控制回路中增加了积分元件以改善系统性能及提高抗干扰能力；
[0076]
基于rslqr控制的飞行控制律可以改善控制系统的动态性能和稳态性能；在设计控制器的rslqr控制时，首先提取角速度模型和垂直速度模型；然后，为角速度和速度环或内环设计rslqr控制器；
[0077]
所述控制器的姿态和高度回路控制采用了pi控制方法以提升控制精度；
[0078]
所述控制器的滚转通道中，其控制结构的pi增益和由内环及外环之间的最佳
阻尼比和带宽匹配关系决定；它们可以通过matlab中的pi参数整定工具箱获得；
[0079]
所述控制器使用扩展状态观测器eso来估计状态和未知的总干扰，然后通过对rslqr的初始控制量进行补偿，得到最终的控制输入，以提高抵抗扰动和不确定因素的能力，
[0080]
通过公式18表述的扰动条件，可以得到下面的二阶非线性系统:
[0081][0082]
其中x1表示姿态或高度的状态变量，f(
·
)是包括模型不确定性和外部干扰的系统总干扰，表示控制输入，b是放大倍数；然后，控制器系统受到的总扰动被扩展成一个新的状态变量x3，并且让新系统可以表达如下:
[0083][0084]
对于控制器扩展后的系统，有以下扩展状态观测器:
[0085][0086]
其中z＝[z1,z2,z3]
t
是扩展状态向量x＝[x1,x2,x3]
t
的估计，β1,β2,β3是观测器增益，非线性函数fal(e,α
i
,δ)可表示为：
[0087][0088]
其中α1、α2和δ是非线性函数fal(
·
)的参数，α表示非线性形状，取α1＝0.5、α2＝0.25，δ决定原点周围线性区间的宽度；观测器参数β
i
决定了状态x
i
的跟踪速度；适当增加β1和β2可以有效抑制β3过多引起的观测器振荡。因此应协调进行这三个参数的调整，通过调整参数以实时观察到扩展状态x3；
[0089]
在得到总扰动的估计值z3后，通过对rslqr控制器输出的扰动补偿,可以得到实时控制量为：
[0090][0091]
通过将公式30代入公式25，非线性控制系统变成线性积分串联系统，这被称为动态补偿线性化，表述为
[0092]
[0093]
与现有技术相比，本发明较好地综合了固定翼飞行器和旋翼飞行器的优点，同时改进了现有的控制系统，使其具有更高的可靠性、抗干扰性和控制性能。
[0094]
本发明采用了固定翼、可倾转旋翼和不可倾转旋翼相结合的结构，它可以在没有跑道的情况下垂直起落；垂直起降时两对旋翼同时运行，巡航时只有位于尾翼根部的一对旋翼运行。通过将旋翼和固定翼结合的方法，不仅增加了飞行器的续航时间，更拓宽了飞行器的工程应用前景。与此同时，本发明提出了一种将鲁棒伺服线性二次调节器最优控制和扩展状态观测器相结合的改进飞行控制律，提高了控制性能和工程可靠性。
[0095]
在工程实践中，pid控制仍然是被广泛使用的，然而pid方法控制的性能并不理想，不能解决实际飞行试验中经常出现的执行器饱和和不确定干扰问题。如何设计一种更好的线性控制器来解决这些实际问题，提高控制性能是本发明的重点。本发明提出了一种基于rslqr和eso相结合的改进飞行控制律来控制新型无人机的飞行。与pid控制相似，本发明所设计的控制器是一种线性控制方法，具有成本低、易于实现的特点。并解决了执行器饱和和不确定扰动问题，提高了实际飞行中的控制性能。因此，所提出的飞行控制律在倾斜旋翼飞行器的工程应用中具有广阔的前景。
附图说明
[0096]
下面结合附图和具体实施方式对本发明进一步详细的说明：
[0097]
附图1是本发明的飞行器结构示意图；
[0098]
附图1a是本发明的飞行器第二旋翼组的旋翼朝向调整示意图；
[0099]
附图2是本发明的飞行器结构对应的参考坐标系的示意图；
[0100]
附图3是本发明基于鲁棒伺服线性二次调节器的控制示意图；
[0101]
附图4是本发明的滚转角控制示意图；
[0102]
附图5是基于拓展状态观测器(eso)的鲁棒伺服线性二次调节器(rslqr)控制示意图；
[0103]
附图6是本发明所述飞行器的工作原理示意图；
[0104]
图中：1-第一旋翼组；2-机身；3-主翼；4-尾翼；5-第二旋翼组；6-连杆机构；7-升降舵；8-方向舵；
具体实施方式
[0105]
如图所示，一种可倾转旋翼的复合结构飞行器，所述飞行器的机身包括用于空中巡航的主翼和尾翼；所述主翼设于机身中段；所述尾翼设于机身尾部；飞行器还设有用于为飞行器提供动力的旋翼；所述旋翼包括设于固定翼处的第一旋翼组，还包括设于机身后部的第二旋翼组；当飞行器起飞或降落时，所述第一旋翼组、第二旋翼组内各旋翼的朝向均为竖向以向机身提供升力，当飞行器处于空中巡航状态时，所述第二旋翼组内的各旋翼朝向调整至水平方向，为飞行器提供推力。
[0106]
所述述第一旋翼组内各旋翼的朝向固定为竖向。
[0107]
所述第一旋翼组内各旋翼固定于主翼前部；第二旋翼组内各旋翼固定于尾翼根部处。
[0108]
所述主翼、尾翼的翼面均包括可变角度的翼面部位，所述主翼以可变角度的翼面
部位形成升降舵；所述尾翼以可变角度的翼面部位形成方向舵；当飞行器处于空中巡航状态时，第一旋翼组内的各旋翼处于停机状态。
[0109]
所述机身尾部设有与第二旋翼组相连的连杆机构；所述连杆机构可同步调整第二旋翼组内各旋翼的朝向，使之在水平与竖向之间切换。
[0110]
第一旋翼组、第二旋翼组均由两个以小转子驱动的旋翼组成；所述飞行器为无人机，无人机的机身载有自动驾驶仪、传感组件和用于与地面站通讯的遥控组件；所述传感组件包括速度传感器、全球定位器、惯性测量单元和压力传感器；自动驾驶仪通过传感组件测量飞行器工况以优化对飞行器的控制。
[0111]
所述飞行器还包括基于线性模型的控制器；所述控制器基于鲁棒伺服线性二次调节器rslqr和扩展状态观测器eso相结合的飞行控制律来控制飞行器的飞行。
[0112]
所述飞行控制律中的动力学模型为非线性动力学模型，其以机身固定框架bff附加到飞行器的重心位置cog来建立坐标系，方法为将惯性固定式框架eff表示为o
g
x
g
y
g
z
g
，其原点设置于起始点；建立四个辅助框架afs的坐标系o
i
x
ti
y
ti
z
ti
(i＝1,2,3,4)，基于对倾斜角度和侧倾角的考虑,z
ti
轴沿着旋翼的螺旋桨轴；x
ti
轴平行于无人机的纵向平面,垂直于z
ti
轴并垂直纸面向外；y
ti
轴由右手定则确定；不同坐标系之间以坐标转换原理设置坐标系之间的变换矩阵为：
[0113][0114]
φ、θ、ψ代表了欧拉角，c和s分别是余弦和正弦函数的符号，η是固定的侧倾角，用于推进系统以提高其可控性，ε是转子的倾斜角度；
[0115]
所述非线性动力学模型可导出为牛顿-欧拉公式，可将惯性固定式框架表示为:
[0116]
[0117]
其中m是飞行器质量，和分别表示惯性固定式框架中的合力矢量和合力矩矢量，v
b
＝[u,v,w]
t
是速度矢量,ω
b
＝[p,q,r]
t
为姿态角速率向量，i
b
为刚体惯性矩阵，可表示如下:
[0118][0119]
机身固定框架中表示的力f和力矩m是由重力、推进系统、空气动力和转子倾斜作用引起的陀螺效应所产生的，它们可以表示为：
[0120][0121]
其中所有的分力和力矩采取下面的形式表示
[0122]
惯性固定式框架中的重力可以表示为：
[0123][0124]
所述第二旋翼组为飞行器在空中巡航时的推进系统，推进系统推进矢量的表示方法为利用辅助框架与机身固定框架bff之间的旋转矩阵，可以将推力矢量沿着机身固定框架分解，得到以下公式，
[0125][0126]
其中，t
ia
为用辅助框架表示的推力矢量，t
i
为推力值，δ
i
为马达节流，g
ti
(
·
)为实验确定的数学关系；由推进系统产生的力矩矢量可以表示为：
[0127][0128]
其中为推力矢量产生的力矩矢量，d
i
是从齿轮到各转子轴的位置矢量，τ
i
表示转子空气阻力引起的力矩，表示辅助框架afs中的力矩矢量，表示机身固定框架(bff)中的力矩矢量；
[0129]
推进系统中旋翼的转子旋转会产生陀螺旋进动力矩效应。该力矩向量的表达式如下：
[0130]
[0131]
其中j
ri
是推进组件绕其轴线的惯性矩，ω
i
代表辅助框架(afs)中转子的旋转角速度矢量；
[0132]
当在飞行模型中引入方向舵因素时，所述飞行器的空气动力和力矩如下:
[0133][0134]
其中，q是动压，α是迎角，β是侧滑角，δ
α
、δ
e
和δ
r
分别是副翼、升降舵和方向舵的偏转角；
[0135]
设ζ＝[x,y,z]
t
表示飞机在惯性固定式框架中的位置向量，则根据坐标系之间的转换关系，平移运动方程和旋转运动方程可以表示为：
[0136][0137]
基于上述内容，飞行模型系统的6自由度非线性动力学方程可以用一阶向量微分方程的形式来描述:
[0138][0139]
其中x是状态变量u,v,w,p,q,r,φ,θ,ψ,x
g
,y
g
,z
g
的向量，u是输入变量的向量，包括马达节流δ1、δ2、δ3和δ4以及操纵面偏转δ
α
、δ
e
、δ
r
，在飞行器从空中巡航转为起降作业时的过渡模式以及飞行器空中巡航时的固定翼模式下被考虑。
[0140]
所述线性控制器基于通道节流和配平计算进行控制分配，具体包括垂直通道δ
h
、俯仰通道δ
θ
、翻滚通道δ
φ
、偏航通道δ
ψ
，
[0141]
四个通道的虚拟控制输入和推进器的实际节流之间的关系建立如下:
[0142][0143]
其中δ
hi
,δ
θi
,δ
φi
,δ
ψi
(i＝1,2,3,4)分别是垂直通道δ
h
、俯仰通道δ
θ
、翻滚通道δ
φ
、偏航通道δ
ψ
的节流阀的重量；
[0144]
当飞行器处于平衡状态时，基于公式11中的非线性动力学方程，可得到下面的扰动平衡方程:
[0145][0146]
其中δ(
·
)＝(
·
)-(
·
)
op
，“op”表示操作点；
[0147]
根据以上描述，四个通道的修整条件可以表示为:
[0148][0149]
设飞行器工作于旋翼飞行器模式时，气动效应器和陀螺效应器的效率低至可忽略不计；设飞行器工作于直升机模式时，ε、θ和φ等于零；设较小的高阶项视为可忽略，则可以得到：
[0150][0151]
其中
[0152]
设第一旋翼组内有两个旋翼，分别由第一电机、第二电机驱动，且由于第一旋翼组、第二旋翼组几何参数不对称，第一和第二电机首先达到最大容量，则可以基于第一电机获得每个通道的权重系数，计算结果如下所示:
[0153][0154]
最后，通道输入和实际节流阀之间的控制分配关系可以通过将公式17代入公式13来获得。
[0155]
当飞行器工作于旋翼飞行器模式时，若需引入状态向量以进行姿态控制和高度控制，则对公式11中的非线性动力学方程进行分割，得到和输入向量此时飞行模型系统可表述为
[0156][0157]
所述飞行模型系统在平衡操作点处被线性化，通过泰勒级数展开并在一阶项中截断。因此，线性化的飞行模型系统以如下公式所示:
[0158][0159]
其中，
[0160]
飞行器模型系统的线性化系统方程可基于公式19进一步表述为
[0161][0162]
其中y
c
是输出向量，c
c
是相应的转移矩阵；
[0163]
基于鲁棒伺服线性二次调节器rslqr的控制方法是在线性二次调节器lqr控制方法的基础上，通过在系统中引入状态偏差而得，此状态偏差可以被调整到零，使得系统状态变量可以精确地跟踪输入命令；
[0164]
如果偏差假定为e＝r
c-y
c
，其中r是控制指令，则飞行器状态方程可以定义为：
[0165][0166]
其中
[0167]
鲁棒伺服线性二次调节器rslqr控制的代价函数由下式给出：
[0168][0169]
其中q和r是权重矩阵；控制器的控制系统选择矩阵r作为单位矩阵，矩阵q作为对
角矩阵；矩阵q中的值使用布赖森bryson定律进行缩放；最后，鲁棒伺服线性二次调节器rslqr控制的增益矩阵可以表示为:
[0170]
k
c
＝[k
i
,k
p
]＝r-1
b
t
p
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(公式23)
[0171]
其中k
i
、k
p
是不同的分块矩阵，它们具有相同的维度e和p(＝p
t
＞0)是下列代数黎卡提方程的解:
[0172]
pa+a
t
p-pbr-1
b
t
p+q＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(公式24)
[0173]
鲁棒伺服线性二次调节器rslqr控制的最佳控制输入如下述公式25所示，
[0174][0175]
所述rslqr控制在状态反馈控制回路中增加了积分元件以改善系统性能及提高抗干扰能力；
[0176]
基于rslqr控制的飞行控制律可以改善控制系统的动态性能和稳态性能；在设计控制器的rslqr控制时，首先提取角速度模型和垂直速度模型；然后，为角速度和速度环或内环设计rslqr控制器；
[0177]
所述控制器的姿态和高度回路控制采用了pi控制方法以提升控制精度；
[0178]
所述控制器的滚转通道中，其控制结构的pi增益和由内环及外环之间的最佳阻尼比和带宽匹配关系决定；它们可以通过matlab中的pi参数整定工具箱获得；
[0179]
所述控制器使用扩展状态观测器eso来估计状态和未知的总干扰，然后通过对rslqr的初始控制量进行补偿，得到最终的控制输入，以提高抵抗扰动和不确定因素的能力，
[0180]
通过公式18表述的扰动条件，可以得到下面的二阶非线性系统:
[0181][0182]
其中x1表示姿态或高度的状态变量，f(
·
)是包括模型不确定性和外部干扰的系统总干扰，表示控制输入，b是放大倍数；然后，控制器系统受到的总扰动被扩展成一个新的状态变量x3，并且让新系统可以表达如下:
[0183][0184]
对于控制器扩展后的系统，有以下扩展状态观测器:
[0185][0186]
其中z＝[z1,z2,z3]
t
是扩展状态向量x＝[x1,x2,x3]
t
的估计，β1,β2,β3是观测器增
益，非线性函数fal(e,α
i
,δ)可表示为：
[0187][0188]
其中α1、α2和δ是非线性函数fal(
·
)的参数，α表示非线性形状，取α1＝0.5、α2＝0.25，δ决定原点周围线性区间的宽度；观测器参数β
i
决定了状态x
i
的跟踪速度；适当增加β1和β2可以有效抑制β3过多引起的观测器振荡。因此应协调进行这三个参数的调整，通过调整参数以实时观察到扩展状态x3；
[0189]
在得到总扰动的估计值z3后，通过对rslqr控制器输出的扰动补偿,可以得到实时控制量为：
[0190][0191]
通过将公式30代入公式25，非线性控制系统变成线性积分串联系统，这被称为动态补偿线性化，表述为
[0192][0193]
实施例1：
[0194]
本例中仅使用一对可倾斜的旋翼来满足推力要求，这意味着更少的机构、更低的成本、更低的电量消耗和更长的飞行时间。如附图1所示，通过四连杆机构，推进系统旋翼3和4可以从垂直位置(ε＝0
°
)倾斜到水平位置(ε＝90
°
)或反向倾斜。当飞行器进入固定翼飞行器模式时，旋翼1和2停止工作；同时，旋翼3和4为飞行器提供动力。本发明采用比普通飞行器更小的转子，以满足巡航飞行期间的低推重比要求，从而减轻飞行器重量并提高巡航效率。
[0195]
实施例2：
[0196]
在飞行器建模工作中，本例让机身固定框架(bff)附加到飞机的重心位置(cog)。将惯性固定式框架(eff)表示为o
g
x
g
y
g
z
g
，其原点设置于起始点。不同于其他类似的工作,建立四个辅助框架(afs)的坐标系o
i
x
ti
y
ti
z
ti
(i＝1,2,3,4)时考虑了倾斜角度和侧倾角,z
ti
轴沿着螺旋桨轴。x
ti
轴平行于无人机的纵向平面,垂直于z
ti
轴并垂直纸面向外。y
ti
轴由右手定则确定。参考坐标系如附图2所示。根据坐标转换原理，给出了坐标系之间的变换矩阵：
[0197][0198]
φ、θ、ψ代表了欧拉角,c和s分别是余弦和正弦函数的符号,η是固定的侧倾角，用于推进系统以提高其可控性，ε是转子的倾斜角度。
[0199]
复合结构飞行器非线性动力学模型可以导出为牛顿-欧拉公式，可将惯性固定式框架表示为:
[0200][0201]
其中m是飞机质量，和分别表示惯性固定式框架中的合力矢量和合力矩矢量，v
b
＝[u,v,w]
t
是速度矢量,ω
b
＝[p,q,r]
t
为姿态角速率向量，i
b
为刚体惯性矩阵，可表示如下:
[0202][0203]
机身固定框架中表示的力和力矩是由重力、推进系统、空气动力和转子倾斜作用引起的陀螺效应所产生的，它们可以表示为：
[0204][0205]
其中所有的分力和力矩采取下面的形式表示。
[0206]
1、重力
[0207]
惯性固定式框架中的重力可以表示为：
[0208]
[0209]
2、推进系统
[0210]
①
推进矢量
[0211]
利用辅助框架与机身固定框架(bff)之间的旋转矩阵，可以将推力矢量沿着机身固定框架分解:
[0212][0213]
其中，t
ia
为用辅助框架表示的推力矢量，t
i
为推力值，δ
i
为马达节流，g
ti
(
·
)为实验确定的数学关系。
[0214]
②
力矩矢量
[0215]
由推进系统产生的力矩矢量可以表示为：
[0216][0217]
其中为推力矢量产生的力矩矢量，d
i
是从齿轮到各转子轴的位置矢量，τ
i
表示转子空气阻力引起的力矩，表示辅助框架afs中的力矩矢量，表示机身固定框架(bff)中的力矩矢量。
[0218]
③
陀螺力矩。
[0219]
旋转转子会产生陀螺旋进动力矩效应。该力矩向量的表达式如下：
[0220][0221]
其中j
ri
是推进组件绕其轴线的惯性矩，ω
i
代表辅助框架(afs)中转子的旋转角速度矢量。
[0222]
④
空气动力和力矩
[0223]
考虑到方向舵，可倾转旋翼的复合结构飞行器的空气动力和力矩如下:
[0224][0225]
其中，q是动压，α是迎角，β是侧滑角，δ
α
、δ
e
和δ
r
分别是副翼、升降舵和方向舵的偏转角。
[0226]
另外，假设ζ＝[x,y,z]
t
表示飞机在惯性固定式框架中的位置向量。根据坐标系之间的转换关系，平移运动方程和旋转运动方程可以表示为：
[0227][0228]
基于上述分析，系统的6自由度非线性动力学方程可以用一阶向量微分方程的形式来描述:
[0229][0230]
其中x是状态变量u,v,w,p,q,r,φ,θ,ψ,x
g
,y
g
,z
g
的向量，u是输入变量的向量，通常包括马达节流δ1、δ2、δ3和δ4以及操纵面偏转δ
α
、δ
e
、δ
r
，它们在过渡模式和固定翼模式下被考虑。
[0231]
实施例3：
[0232]
本例在设计控制器时，采用以下方法：
[0233]
①
基于通道节流和配平计算的控制分配策略
[0234]
为本发明所述的可倾转旋翼的复合结构飞行器，提出了一种基于通道节流和配平计算的控制分配方法。首先，四个通道的虚拟控制输入和推进器的实际节流之间的关系建立如下:
[0235][0236]
其中δ
hi
,δ
θi
,δ
φi
,δ
ψi
(i＝1,2,3,4)分别是垂直通道δ
h
、俯仰通道δ
θ
、翻滚通道δ
φ
、偏航通道δ
ψ
的节流阀的重量。
[0237]
当飞机处于平衡状态，即基于非线性动力学方程(11)，容易地得到下面的扰动平衡方程:
[0238][0239]
其中δ(
·
)＝(
·
)-(
·
)
op
，“op”表示操作点。
[0240]
根据以上描述，四个通道的修整条件可以表示为:
[0241][0242]
在解方程之前，需要做以下假设。(1)旋翼飞行器模式下，气动效应器和陀螺效应器的效率很低，因此可以忽略不计。(2)假设在直升机模式下，ε、θ和φ等于零。(3)忽略较小的高阶项，可以得到：
[0243][0244]
其中
[0245]
由于几何参数不对称，第一和第二电机首先达到最大容量。因此，可以基于第一电机获得每个通道的权重系数,计算结果如下所示:
[0246][0247]
最后，通道输入和实际节流阀之间的控制分配关系可以通过将式(17)代入式(13)
来获得。
[0248]
②
线性化模型
[0249]
为了在旋翼飞行器模式下设计姿态和高度控制器，考虑到状态向量，对非线性模型(11)进行分割，得到和输入向量这产生了一个新的系统模型:
[0250][0251]
由于控制器是基于线性模型设计的，系统(18)在平衡操作点附近被线性化，通过泰勒级数展开它并在一阶项中截断。因此，线性化模型如下所示:
[0252][0253]
其中，
[0254]
③
鲁棒伺服线性二次调节器(rslqr)控制。
[0255]
基于模型(19)，飞行器的线性化系统方程由下式给出:
[0256][0257]
其中y
c
是输出向量，c
c
是相应的转移矩阵。
[0258]
鲁棒伺服线性二次调节器rslqr控制方法是在线性二次调节器lqr控制方法的基础上，通过在系统中引入状态偏差作为新的变量而发展起来的。这样，偏差可以被调整到零，使得系统状态变量可以精确地跟踪输入命令。如果偏差假定为e＝r
c-y
c
，其中r是控制指令。新的状态方程可以定义为：
[0259][0260]
其中
[0261]
基于新系统的鲁棒伺服线性二次调节器rslqr控制的代价函数由下式给出：
[0262][0263]
其中q和r是权重矩阵。选择加权矩阵来表征控制设计的性能，但适用于这些已选矩阵的技术还不成熟。为了便于工程应用，根据控制系统的要求，选择矩阵r作为单位矩阵，矩阵q作为对角矩阵。矩阵q中的值使用布赖森bryson定律进行缩放。最后，鲁棒伺服线性二次调节器rslqr控制的增益矩阵可以表示为:
[0264]
k
c
＝[k
i
,k
p
]＝r-1
b
t
p
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(公式23)
[0265]
其中k
i
、k
p
是不同的分块矩阵，它们具有相同的维度e和p(＝p
t
＞0)是下列代数黎卡提方程的解:
[0266]
pa+a
t
p-pbr-1
b
t
p+q＝0
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(公式24)
[0267]
鲁棒伺服线性二次调节器rslqr控制的最佳控制输入如等式(25)所示，鲁棒伺服线性二次调节器rslqr状态反馈控制的示意图附图3所示:
＝0.25，δ决定原点周围线性区间的宽度。如果太大，就无法跟踪大幅度的扰动信号。相比之下，原点附近容易出现高频振荡。观测器参数β
i
决定了状态x
i
的跟踪速度。此外，这些参数是相互制约的。适当增加β1和β2可以有效抑制β3过多引起的观测器振荡。因此应协调进行这三个参数的调整，通过不断调整这些参数，观察者可以实时观察到状态，尤其是扩展状态x3。控制结构如附图5所示。
[0281]
在得到总扰动的估计值z3后，通过对rslqr控制器输出的扰动补偿,可以得到实时控制量为：
[0282][0283]
通过将等式(30)代入系统(25)，非线性控制系统变成线性积分串联系统，这被称为动态补偿线性化[31]:
[0284]

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除