连挂机车车钩转角的计算方法与流程

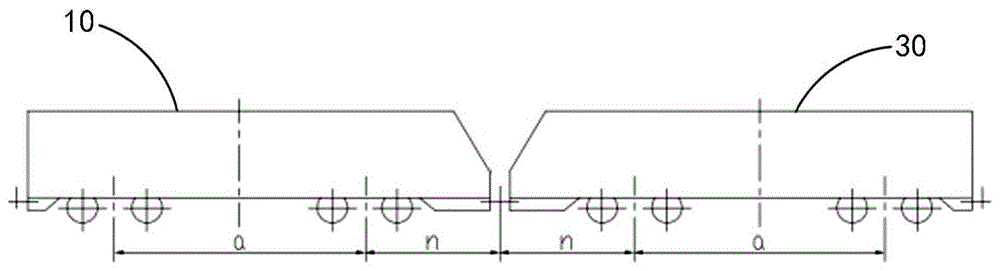
本发明总体来说涉及连挂机车技术领域，具体而言，涉及一种连挂机车车钩转角的计算方法。

背景技术：

连挂机车过曲线时，影响机车车钩转角主要是两个因素，其一是曲线线路的半径，其二是机车横动量。现有技术中存在的连挂机车车钩转角的计算方法，并不能直观地表达曲线半径、机车横动量以及车钩转角三者之间的关系。

在所述背景技术部分公开的上述信息仅用于加强对本发明的背景的理解，因此它可以包括不构成对本领域普通技术人员已知的现有技术的信息。

技术实现要素：

本发明的一个主要目的在于提供一种连挂机车车钩转角的计算方法，能够清晰且直观地表达出曲线半径、机车横动量和车钩转角三者之间的关系，为机车车钩-横动量系统的匹配提供了有力支撑。

为实现上述发明目的，本发明采用如下技术方案：

根据本发明的一个方面，提供了一种连挂机车车钩转角的计算方法，包括如下步骤：

确定机车的第一运行姿态和第二运行姿态；

基于所述第一运行姿态，获得车钩转动中心点相对于机车的第一偏移量；

基于所述第二运行姿态，获得车钩转动中心点相对于机车的第二偏移量；以及

基于所述第一偏移量和所述第二偏移量，获得车钩转角；

其中，所述第一运行姿态为在不考虑机车横动量的工况下，机车处于曲线线路上的理想位置；所述第二运行姿态为基于机车处于曲线线路上的理想位置，根据机车横动量所获得的机车的实际位置。

根据本发明的一些实施方式，所述获得车钩转动中心点相对于机车的第一偏移量，包括：

根据如下公式获得所述第一偏移量，

其中，cl代表第一偏移量，a代表机车转向架中心距，n代表车钩转动中心点与相邻机车转向架中心之间的距离，r代表曲线线路的曲线半径。

根据本发明的一些实施方式，所述获得车钩转动中心点相对于机车的第二偏移量，包括：

根据如下公式获得所述第二偏移量，

其中，ch代表第二偏移量，a代表机车转向架中心距，n代表车钩转动中心点与相邻转向架中心之间的距离，δ代表机车横动量。

根据本发明的一些实施方式，连挂机车包括第一机车和第二机车，所述第一机车的尾部设有第一车钩，所述第二机车的头部设有第二车钩；所述基于所述第一偏移量和所述第二偏移量，获得车钩转角，包括：

在所述第一机车处于所述第二运行姿态时，获得所述第一车钩的转动中心点与所述第一机车的中心点之间的第一连线，以及获得所述第一车钩的转动中心点与曲线半径圆心之间的第二连线；基于所述第一连线和所述第二连线，获得所述第一连线和所述第二连线之间的第一夹角；

获得所述第一车钩的转动中心点与所述第二车钩的转动中心点之间的第三连线，基于所述第二连线和所述第三连线，获得所述第二连线和所述第三连线之间的第二夹角；

基于所述第一夹角和所述第二夹角，获得所述第一车钩的车钩转角。

根据本发明的一些实施方式，所述获得所述第一连线和所述第二连线之间的第一夹角，包括：

在所述第一机车处于所述第一运行姿态时，获得所述第一车钩的转动中心点分别到所述第一机车的中心点的连线和曲线半径圆心的连线之间的第一子夹角；

获得所述第一机车分别处于第一运行姿态和所述第二运行姿态时的车身的第二子夹角；

基于所述第一子夹角和所述第二子夹角，获得所述第一夹角。

根据本发明的一些实施方式，所述获得所述第二连线和所述第三连线之间的第二夹角，包括：

获得所述第二连线的距离；

获得所述第三连线的距离；

获得所述第二车钩的转动中心点与曲线半径圆心之间的距离；

基于所述第二连线的距离、所述第三连线的距离以及所述第二车钩的转动中心点与曲线半径圆心之间的距离，根据余弦定理，获得所述第二夹角的余弦值。

根据本发明的一些实施方式，所述方法还包括：

在所述第二机车处于所述第二运行姿态时，获得所述第二车钩的转动中心点与所述第二机车的中心点之间的第四连线，以及所述第二车钩的转动中心点与曲线半径圆心之间的第五连线，基于所述第四连线和所述第五连线，获得所述第四连线和所述第五连线之间的第三夹角；

基于所述第三连线和所述第五连线，获得所述第三连线和所述第五连线之间的第四夹角；

基于所述第三夹角和所述第四夹角，获得所述第二车钩的车钩转角。

根据本发明的一些实施方式，所述获得所述第四连线和所述第五连线之间的第三夹角，包括：

在所述第二机车处于所述第一运行姿态时，获得所述第二车钩的转动中心点分别到所述第二机车的中心点的连线和曲线半径圆心的连线之间的第三子夹角；

获得所述第二机车分别处于所述第一运行姿态和所述第二运行姿态时的车身的第四子夹角；

基于所述第三子夹角和所述第四子夹角，获得所述第二夹角。

根据本发明的一些实施方式，所述获得所述第三连线和所述第五连线之间的第四夹角，包括：

获得所述第二连线的距离；

获得所述第三连线的距离；

获得所述第五连线的距离；

基于所述第二连线的距离、所述第三连线的距离以及所述第五连线的距离，根据余弦定理，获得所述第四夹角的余弦值。

根据本发明的一些实施方式，所述第一运行姿态为所述机车处于曲线线路上的最小曲线半径的理想位置；所述第二运行姿态为所述机车横动量为最大横动量。

上述发明中的一个实施例具有如下优点或有益效果：

本发明实施例的连挂机车车钩转角的计算方法，将车钩转动中心点的偏移量分为了两个部分，分别是机车处于第一运行姿态下的偏移量和机车处于第二运行姿态下的偏移量，通过这样的方式，可以清晰且直观地表达出曲线半径、机车横动量和车钩转角三者之间的关系，为机车车钩-横动量系统的匹配提供了有力支撑。同时，在已知车钩转角(已确定车钩类型)的情况下，能够合理配合机车横动量，并且，也可在已知机车横动量的情况下，合理安排车钩的选型。

附图说明

通过参照附图详细描述其示例实施方式，本发明的上述和其它特征及优点将变得更加明显。

图1是根据一示例性实施方式示出的一种连挂机车的示意图。

图2是根据一示例性实施方式示出的连挂机车分别处于第一运行姿态和第二运行姿态的示意图。

图3是根据一示例性实施方式示出的车钩转角示意图。

其中，附图标记说明如下：

10、第一机车

30、第二机车

50、曲线线路

具体实施方式

现在将参考附图更全面地描述示例实施方式。然而，示例实施方式能够以多种形式实施，且不应被理解为限于在此阐述的实施方式；相反，提供这些实施方式使得本发明将全面和完整，并将示例实施方式的构思全面地传达给本领域的技术人员。图中相同的附图标记表示相同或类似的结构，因而将省略它们的详细描述。

虽然本说明书中使用相对性的用语，例如“上”、“下”来描述图标的一个组件对于另一组件的相对关系，但是这些术语用于本说明书中仅出于方便，例如根据附图中所述的示例的方向。能理解的是，如果将图标的装置翻转使其上下颠倒，则所叙述在“上”的组件将会成为在“下”的组件。其他相对性的用语，例如“顶”、“底”等也作具有类似含义。用语“一个”、“一”、“该”和“所述”用以表示存在一个或多个要素/组成部分/等；用语“包括”和“具有”用以表示开放式的包括在内的意思并且是指除了列出的要素/组成部分/等之外还可存在另外的要素/组成部分/等；用语“第一”、“第二”、“第三”和“第四”等仅作为标记使用，不是对其对象的数量限制。

本发明的发明人在研究中发现，连挂机车过曲线时，影响机车车钩转角主要是两个因素，其一是曲线线路半径，其二是机车横动量。现有技术中存在的连挂机车车钩转角的计算方法，并不能直观地表达曲线半径、机车横动量以及车钩转角三者之间的关系。

基于此，本发明提出一种连挂机车车钩转角的计算方法，包括如下步骤：确定机车的第一运行姿态和第二运行姿态；基于所述第一运行姿态，获得车钩转动中心点相对于机车的第一偏移量；基于所述第二运行姿态，获得车钩转动中心点相对于机车的第二偏移量；基于所述第一偏移量和所述第二偏移量，获得车钩转角；其中，所述第一运行姿态为在不考虑机车横动量的工况下，机车处于曲线线路上的理想位置；所述第二运行姿态为基于机车处于曲线线路上的理想位置，根据机车横动量，获得机车的实际位置。

本发明实施例的连挂机车车钩转角的计算方法，将车钩转动中心点的偏移量分为了两个部分，分别是机车处于第一运行姿态下的偏移量和机车处于第二运行姿态下的偏移量，通过这样的方式，可以清晰且直观地表达出曲线半径、机车横动量和车钩转角三者之间的关系，为机车车钩-横动量系统的匹配提供了有力支撑。同时，在已知车钩转角(已确定车钩类型)的情况下，能够合理匹配机车横动量，并且，也可在已知机车横动量的情况下，合理安排车钩的选型。

下面结合附图，详细说明本发明提出的连挂机车车钩转角的计算方法的详细过程。

如图1所示，图1是根据一示例性实施方式示出的一种连挂机车的示意图。在一示例实施方式中，连挂机车包括第一机车10和第二机车30，第一机车10的尾部设有第一车钩(前车钩)，第二机车30的头部设有第二车钩(后车钩)，第一车钩与第二车钩相连接，实现第一机车10和第二机车30的重联运行。

第一机车10的转向架中心距为a，第二机车30的转向架中心距为a，第一车钩和第二车钩的转动中心距相邻转向架中心的距离为n。关于转向架中心距a以及车钩的转动中心距相邻转向架中心的距离n的具体应用将在后续图3中详细说明。

如图2所示，图2是根据一示例性实施方式示出的连挂机车分别处于第一运行姿态和第二运行姿态时的示意图。其中，图2中虚线代表机车处于第一运行姿态，图2中实线代表机车处于第二运行姿态。如图2所示，用机车的纵向中心线代表机车，具体来说，图2中虚线的长度或实线的长度代表机车沿纵向的距离。

第一运行姿态是忽略机车横动量的影响，将机车置于曲线线路50上，此时机车处于曲线线路50上的理想位置(如图2中虚线所示)。

第二运行姿态是在机车处于理想位置的情况下，进一步考虑机车横动量，基于机车横动量，确定机车的实际位置(如图2中实线所示)。

在图2中，p代表机车的中心点，a’代表机车处于第一运行姿态时与曲线线路50的交叉点，aa’代表机车横动量，eb’代表基于第一运行姿态，车钩转动中心点相对于机车的第一偏移量，bb’代表基于第二运行姿态，车钩转动中心点相对于机车的第二偏移量。

当机车处于第一运行姿态时，图2中虚线为机车理想状态下的车体位置，eb’即为仅在曲线线路50的影响下，车钩转动中心点出现的第一偏移量。

当机车处于第二运行姿态时，图2中实线为机车在机车横动量工况下的车体偏斜位置，bb’即为在机车横动量的影响下，车钩转动中心点出现的第二偏移量。

结合图1和图2可知，机车转向架中心距为a，车钩转动中心点与相邻转向架中心的距离为n，则有图2中的pa’为a/2，a’b’为n，

根据相似三角形原理，基于机车处于第一运行姿态下，曲线线路50引起的第一偏移量为：

其中，cl代表第一偏移量，a代表机车转向架中心距，n代表车钩转动中心点与相邻机车转向架中心之间的距离，r代表曲线线路50上的曲线半径。

设机车横动量为δ，根据三角形原理，基于机车处于第二运行姿态下，机车横动量引起的第二偏移量为：

其中，ch代表第二偏移量，a代表机车转向架中心距，n代表车钩转动中心点与相邻转向架中心之间的距离，δ代表机车横动量。

如图3所示，图3是根据一示例性实施方式示出的车钩转角示意图。图3示出的是如图1所示的两个机车之间转角的示意图，第一机车10的尾部设有第一车钩，第二机车30的头部设有第二车钩，第一车钩与第二车钩相连接，实现第一机车10和第二机车30的重联运行。

虚线110代表第一机车10处于第一运行姿态时的示意图，实线120代表第一机车10处于第二运行姿态时的示意图。虚线310代表第二机车30处于第一运行姿态时的示意图，实线320代表第二机车30处于第二运行姿态时的示意图。第一机车10和第二机车30具有相同的运行姿态，第一机车10处于最大机车横动量的位置，第二机车30也处于最大机车横动量的位置，故连挂机车处于曲线线路50上的极限位置，此时车钩呈z字型，且具有最大的车钩转角。

如图3所示，在确定了连挂机车在曲线线路50上的极限运行姿态之后，依据三角形几何原理，可获得第一车钩和第二车钩的转角，其中，γ1代表第一车钩的车钩转角，γ2代表第二车钩的车钩转角。连挂车钩总长度为线段bc，用l表示。根据三角形几何关系，则有如下公式：

其中，∠pbo为第一夹角，即为第一车钩的转动中心点(b)与第一机车的中心点(p)之间的第一连线(pb)以及第一车钩的转动中心点(b)与曲线半径圆心(o)之间的第二连线(bo)之间的夹角。

同理，∠obc为第二夹角，即为第一车钩的转动中心点(b)与第二车钩的转动中心点(c)之间的第三连线(bc)以及第二连线(bo)之间的夹角。

同理，∠ocq为第三夹角，即为第二车钩的转动中心点(c)与第二机车的中心点(q)之间的第四连线(cq)以及第二车钩的转动中心点(c)与曲线半径圆心(o)之间的第五连线(co)之间的夹角。

同理，∠ocb为第四夹角，即为第三连线(bc)和第五连线(co)之间的夹角。

由公式(1)可知，∠pbo＝∠pb’o-∠bpb’，∠pb’o即为第一车钩的转动中心点(b’)分别到第一机车的中心点(p)和曲线半径圆心(o)连线之间的第一子夹角。∠bpb’即为第一机车分别处于第一运行姿态和第二运行姿态时的车身的第二子夹角。

进一步由公式(1)可知，获得ob、bc和oc的距离后，根据余弦定理，即可获得∠obc的余弦值。

同理，公式(1)可知，∠ocq＝∠qc’o+∠cqc’，∠qc’o即为第二机车30处于第一运行姿态时，第二车钩的转动中心点(c’)分别到第二机车的中心点(q)和曲线半径圆心(o)连线之间的第三子夹角。∠cqc’即为第二机车30分别处于第一运行姿态和第二运行姿态时的车身的第四子夹角。

同理，进一步由公式(1)可知，获得ob、bc和oc的距离后，根据余弦定理，即可获得∠ocb的余弦值。

对于△pbo和△pb’o，由于两个三角形共用一个∠pob，则有如下公式：

基于图2中获得的第一偏移量和第二偏移量，可知：

pb’＝qc’＝a/2+n，ob’＝oc’＝r+带入公式(2)，则有：

由于aa’为机车横动量，设为δ，pa’＝a/2，带入公式(2)，则有

由公式(2)进一步可得：

∠pbo＝arccos∠pb′o-arctan∠bpb′

∠qco＝arccos∠qc′o-arctan∠cqc′

根据三角函数关系：

并根据图2中确定的第一偏移量和第二偏移量可得如下公式：

化解可得出：

至此，将获得的已知量分别带入公式(2)和公式(1)，即可获得γ1和γ2，其中γ1和γ2的结果中已通过机车横动量δ表达。

综上所述，本发明的连动机车车钩转角的计算方法的优点和有益效果在于：

本发明实施例的连挂机车车钩转角的计算方法，将车钩转动中心点的偏移量分为了两个部分，分别是机车处于第一运行姿态下的偏移量和机车处于第二运行姿态下的偏移量，通过这样的方式，可以清晰且直观地表达出曲线半径、机车横动量和车钩转角三者之间的关系，为机车车钩-横动量系统的匹配提供了有力支撑。同时，在已知车钩转角(已确定车钩类型)的情况下，能够合理配合机车横动量，并且，也可在已知机车横动量的情况下，合理安排车钩的选型。

在此应注意，附图中示出而且在本说明书中描述的连挂机车车钩转角的计算方法仅仅是采用本发明的原理的一个示例。本领域的普通技术人员应当清楚地理解，本发明的原理并非仅限于附图中示出或说明书中描述的装置的任何细节或任何部件。

应可理解的是，本发明不将其应用限制到本说明书提出的部件的详细结构和布置方式。本发明能够具有其他实施方式，并且能够以多种方式实现并且执行。前述变形形式和修改形式落在本发明的范围内。应可理解的是，本说明书公开和限定的本发明延伸到文中和/或附图中提到或明显的两个或两个以上单独特征的所有可替代组合。所有这些不同的组合构成本发明的多个可替代方面。本说明书所述的实施方式说明了已知用于实现本发明的最佳方式，并且将使本领域技术人员能够利用本发明。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除