一种在复杂交路条件下计算列车可行折返时间的方法与流程
 2021-02-05 23:02:56|
2021-02-05 23:02:56| 175|
175| 起点商标网
起点商标网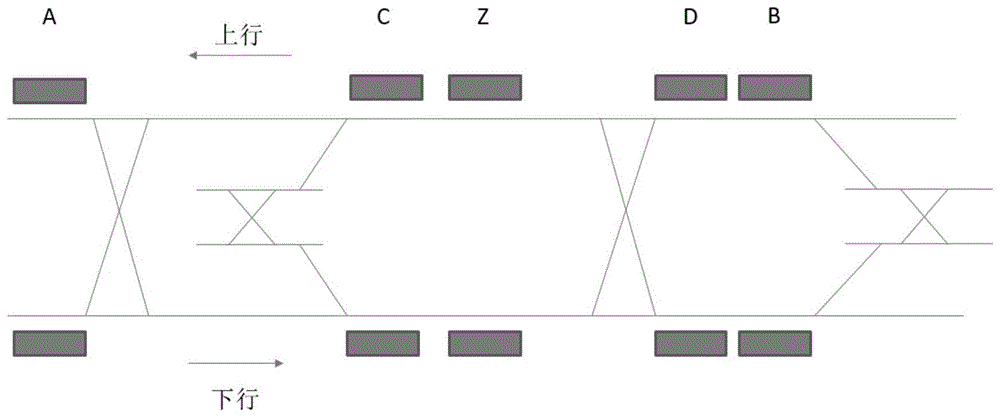
本发明涉及轨道交通技术领域,具体涉及折返时间算法。
背景技术:
现有的计算折返时间算法,主要是根据公式;
(1)全周转时间=车底数*间隔
(2)全周转时间=上行运行时间+下行运行时间+上行折返时间+下行折返时间
上述公式只能计算简单交路的折返时间,未见其他已发表的计算复杂交路折返时间的算法。
在实际运营中,线路的形态多种多样,包括x型,y型,环形,折返的形式分为站前和站后折返,折返轨的数量也有不同,一般为单折返轨或双折返轨,根据客流需要,可能使用不同的发车间隔以及大小交路,有些线路甚至使用三种不同的交路,无法直接使用上述公式计算折返时间。
技术实现要素:
本发明所要解决的技术问题就是提供一种在复杂交路条件下计算列车可行折返时间的方法,不仅能计算简单交路的折返时间,也能计算复杂交路折返时间。
为解决上述技术问题,本发明采用如下技术方案:一种在复杂交路条件下计算列车可行折返时间的方法,包括如下步骤:
s1:根据开行列车运行的线路区间及在该线路区间内对应设置的站场,确定开行的交路、开行比、追踪间隔、完整周期,并根据选取的基准站,计算所有上行列车线和下行列车线;
s2:运用铺点算法进行计算,对于每个可能的δ,计算在此条件下,是否能连接各折返点的列车线;
s3:运用连接算法进行计算,在所有的折返点,为每条到达列车线,匹配发车列车线,分为单轨折返和双轨折返分别计算;
s4:计算车底数,按是否套跑,分为非套跑交路车底数的计算和套跑交路车底数的计算;
s5:优选折返方案,根据所需车底数尽可能少且各折返点的余量尽可能小的原则确定最优折返方案。
进一步的,步骤s1中:开行的交路包括大交路r1和小交路r2,则开行比为r1∶r2,追踪间隔为i,当开行比r1∶r2=1∶2,则完整周期为3i,选取大交路和小交路的共线车站z为基准站,计算所有上行列车线和下行列车线,其中:r1为基准交路,r11u为r1上行列车线,r11d为r1下行列车线,r21u为r2第一单程上行列车线,r21d为r2第一单程下行列车线,r22u为r2第二单程上行列车线,r22d为r2第二单程下行列车线;考虑r11u与r11d的列车线配合,定义任意一对相邻的r11u与r11d在z站的发点时间差为δ∈[0,3i)。
进一步的,步骤s2包括计算从基准车站z到各折返点的时间,其中,从基准车站z到折返点a的时间如下:
如果不可达,记为0,如果方向相反,记为负数;
从基准车站z到其他各折返点的时间计算方法与折返点a相同;
对于运行时间为正以及负的折返点,为可铺点折返点,对于所有可铺点折返点进行铺画。
进一步的,如果只使用其一站台折返,则在该站台铺点即可,如果要使用两个站台交替折返,则两个站台都需考虑,先统一铺在其中某一站台,如果冲突再尝试将点换到另一站台进行尝试。
进一步的,步骤s2中,对于单轨折返,如果:
同时存在发点和到点,且发点–到点≥最小折返时间,此时本列车线可连接,记录下接续的交路代号,并继续连接后续列车线以及其他折返点的列车线;
同时存在发点和到点,且发点–到点<最小折返时间,此时本列车线无法连接,由于是单折返轨,无论后续是到点,发点还是停站通过,均无法成功连接,因此,参数δ无法形成可行的折返方案,放弃此δ,不再连接后续列车线以及其他折返点的列车线,更新δ←δ+1,重新进行铺点和连接算法;
同时存在两个发点,列车线无法连接,放弃此δ;
同时存在发点和停站通过,列车线无法连接,放弃此δ。
进一步的,步骤s2中,对于双轨折返,在折返点可能的序列有:
折返点1:同时存在发点和到点,且发点–到点≥最小折返时间,此时本列车线可连接;
折返点1:同时存在发点和到点,且发点–到点<最小折返时间,列车线在折返点1无法连接,将此发点移动到折返点2,继续向后搜索可行的发点,在此过程中遇到的到点和发点均移动到折返点2,如果此过程中遇到停站线,则此方案δ不可行,放弃;
折返点1:同时存在两个到点,列车线在折返点1无法连接,将此发点移动到折返点2,继续向后搜索可行的发点,在此过程中遇到的到点和发点均移动到折返点2,如果此过程中遇到停站线,则此方案δ不可行,放弃;
折返点1:同时存在到点和停站通过,将到点移动到折返点2,同时搜索折返点1后续的首个发点,也移动到折返点2;
根据上述算法成功连接完折返点1的列车线后,转到折返点2,从首个到点开始连接,方法同单折返轨算法,直到所有列车线连接成功。
进一步的,步骤s4中,非套跑交路车底数的计算方法如下:
开行比r1:r2=m:n
r1对应的详细交路为r11,r12,…,r1m
r2对应的详细交路为r21,r22,…,r2n
分别计算各详细交路的全周转时间t上行+t下行+t上折+t下折
r11全周转时间为t11,所需车底数为
所有交路需要的车底数为
进一步的,步骤s4中,套跑交路车底数的计算方法如下:
开行的交路为:a-b大交路,记为r1,b-c小交路,记为r3,开行比r1:r3=2:1,追踪间隔i
r11u为r1第一单程的上行列车线,r11d为r1第一单程的下行列车线
r12u为r1第二单程的上行列车线,r12d为r1第二单程的下行列车线
r31u为r3的上行列车线,r31d为r3的下行列车线
其中下标(0)、(1)表示周期数,上下行分别编号
应用列车连接算法,可以获得一个完整周期的列车线接续序列,并分别计算全周转时间,r11u的全周转时间t11u,r12u的全周转时间t12u,r31u的全周转时间t31u,
则总车底数为
进一步的,对于每个交路的每个折返点,分别计算折返余量,以车站a作为折返点,t11a折为交路r1在车站a的折返时间,t11a发到为交路r1在车站a的发到间隔,ta最小折为站台a▲的最小折返时间,ta最小发到为站台a▲的最小发到间隔,
t11a中点=(t11a折+t11a发到-ta最小折-ta最小发到)/2
t11a余量=|t11a中点-(t11a折-ta最小折)|
总余量=t11a余量+t21c余量+t22c余量+t11b余量+t21d余量+t22d余量。
本发明采用上述技术方案,首先,基于上下行列车线在基准车站的偏移铺画折返站的到发点,覆盖所有可能的列车线基本结构;其次,连接算法考虑了各种线路形态(x型,y型线路)、折返方式(站前/站后)和开行比,包括交路套跑;最后,基于余量的优选方法,可自动选出较优的折返方案。
因而,具有如下有益效果:确定各折返站的折返时间是自动编制轨道交通运行图的重要前提,因而,通过本发明可以极大的提高编图效率。
本发明的具体技术方案及其有益效果将会在下面的具体实施方式中进行详细的说明。
附图说明
下面结合附图和具体实施方式对本发明作进一步描述:
图1是站场平面图;
图2是开行比示意图;
图3是车站a、d的铺点示意图;
图4是非套跑交路车底数计算示意图;
图5是套跑交路车底数计算示意图;
图6是余量计算示意图。
具体实施方式
下面对本发明实施例的技术方案进行解释和说明,但下述实施例仅为本发明的优选实施例,并非全部。基于实施方式中的实施例,本领域技术人员在没有做出创造性劳动的前提下所获得其他实施例,都属于本发明的保护范围。
在实际运营中,线路的形态多种多样,包括x型,y型,环形,折返的形式分为站前和站后折返,折返轨的数量也有不同,一般为单折返轨或双折返轨,根据客流需要,可能使用不同的发车间隔以及大小交路,有些线路甚至使用三种不同的交路,因此,本发明提供一种在复杂交路条件下计算可行折返时间的方法,可以处理上述所有的复杂性。
一、站场概况和开行交路
列车运行的线路区间及设置的站场如图1所示,开行的交路为:a-b大交路,记为r1,c-d小交路,记为r2。
如图2所示,开行比r1:r2=1:2,追踪间隔i,完整周期为3i,即列车线以此周期重复固定模式。其中,涉及的技术术语解释如下:
共线车站:大小交路都会经过的车站。
开行比:同一时间段内,不同交路列车的开行数量通常要保持一个比例关系(如1:1,1:2,2:2)。
追踪间隔:在共线车站,前后车发车时间的间隔。
完整周期:共线车站完成一个开行比周期的时间,如开行比为1:2,则完整周期为(1+2=3)个追踪间隔。
参考图3所示,选取共线车站z为基准站,r1为基准交路,其中,
r11u为r1的上行列车线,r11d为r1的下行列车线,
r21u为r2第一单程的上行列车线,r21d为r2第一单程的下行列车线,
r22u为r2第二单程的上行列车线,r22d为r2第二单程的下行列车线,
后缀(0)表示第一周期,(1)表示第二周期。
二、铺点算法
考虑r11u与r11d的列车线配合,定义任意一对相邻的r11u与r11d在z站的发点时间差为δ∈[0,3i),对于每个可能的δ,计算在此条件下,是否能连接各折返点的列车线。
对于各交路,从基准车站z到各折返点的时间如下:
折返点a
其他折返点类似。有了上述时间和δ,就可以通过基准车站z的基准时间点计算折返点的到发时间。
特别的,车站d根据使用折返站台的不同,时间计算有所不同。如果只使用其一站台折返,则在该站台铺点即可。如果要使用两个站台交替折返,则两个站台都需考虑,可先统一铺在其中某一站台,如果冲突再尝试将点换到另一站台进行尝试。
参考图3所示,折返点a的铺点过程如下:
1、选取可到达a的交路,如r1,以及起始列车线r11u(0)。
2、记r11u(0)在z站的发点为t0,则该列车线在a站的投影点(到点)为
由于
3、计算反方向列车线在a的投影,r11d(0)在z站的发点为t0+δ,在a的投影点(发点)为
4、如果p1<p2,则从p2开始向左计算(但不铺画)发点,直到pm<p1,然后从pm开始向右计算(但不铺画)发点,直到pn>p1,从pn开始,我们向右铺画两个完整周期(6i)的发点。
5、如果p1≥p2,则从p2开始向右计算(但不铺画)发点,直到pn>p1,从pn开始,我们向右铺画两个完整周期(6i)的发点。
至此,我们在折返点a铺画了两个完整周期的到发点。
参考图3所示,折返点d的铺点过程如下:
1、选取可到达d的交路,如r1,以及起始列车线r11d(0)。
2、记r11d(0)在z站的发点为t0+δ,则该列车线在d站下行站台的投影点(停站线)为
3、计算反方向列车线在d的投影,r11u(0)在z站的发点为t0,在d站上行站台的投影点(停站线)为
4、如果q1到点<q2发点,则从q2开始向左计算(但不铺画),直到qm<q1到点,然后从qm开始向右计算(但不铺画),直到qn>q1,从qn开始,我们向右铺画两个完整周期(6i)。
5、如果q1到点≥q2发点,则从q2开始向右计算(但不铺画),直到qn>q1到点,从qn开始,我们向右铺画两个完整周期(6i)。
至此,在折返点d铺画了两个完整周期的到发点及停站线。如图3,圆圈为在a、d站实际铺画的点。
本领域技术技术人员可以理解的是,上述铺点算法列出了所有可能的情况,对于车站a的折返点a,只有一个站台,对于车站d,有两个站台,或者只使用其一站台折返,或者使用两个站台交替折返,其他的折法点按照不同的情况,参考上述铺点算法即可。
三、连接算法
在所有的折返点,需要为每条到达列车线,匹配发车列车线。
以下描述中,使用/表示到点,\表示发点,--表示停站通过。
3.1单折返轨
在折返点可能的序列有:
1.同时存在发点和到点:/\,且发点–到点>=最小折返时间。
此时本列车线可连接,记录下接续的交路代号,如r11u接r11d,折返轨道a▲,折返时间=发点–到点,与后续列车的发到间隔=下一到点–本发点可继续连接后续列车线以及其他折返点的列车线。
2.同时存在发点和到点:/\,且发点–到点<最小折返时间。
列车线无法连接,由于是单折返轨,无论后续是到点,发点还是停站通过,均无法成功连接,因此,参数δ无法形成可行的折返方案,放弃此δ,不再连接后续列车线以及其他折返点的列车线。更新δ←δ+1,重新进行铺画和连接算法。
3.同时存在两个发点://。
列车线无法连接,放弃此δ。
4.同时存在发点和停站通过:/--。
列车线无法连接,放弃此δ。
3.2双折返轨
在折返点可能的序列有:
1.折返点1,同时存在发点和到点:/\,
发点–到点>=最小折返时间
列车线可连接。
2.折返点1,同时存在发点和到点:/\,
发点–到点<最小折返时间
列车线在折返点1无法连接,可将此发点移动到折返点2,继续向后搜索可行的发点,在此过程中遇到的到点和发点均移动到折返点2,如果此过程中遇到停站线,则此方案δ不可行,放弃。
3.折返点1,同时存在两个发点://,
处理方式同2,即将此发点移动到折返点2,继续向后搜索可行的发点,在此过程中遇到的到点和发点均移动到折返点2,如果此过程中遇到停站线,则此方案δ不可行,放弃。
4.折返点1,同时存在发点和停站通过:/--,
将到点移动到折返点2,同时搜索折返点1后续的首个发点,也移动到折返点2。
根据上述算法成功连接完折返点1的列车线后,转到折返点2,从首个到点开始连接,方法同单折返轨算法,直到所有列车线连接成功。
四、计算车底数
4.1非套跑交路车底数的计算
参考图4所示,开行比r1:r2=m:n=1:2
r1对应的详细交路为r11,r12,…,r1m,具体到图上为r11
r2对应的详细交路为r21,r22,…,r2n,具体到图上为r21,r22
分别计算各详细交路的全周转时间t上行+t下行+t上折+t下折
r11全周转时间为t11,所需车底数为
所有交路需要的车底数为
4.2套跑交路车底数的计算
图5开行的交路为:a-b大交路,记为r1,b-c小交路,记为r3,开行比r1:r3=2:1,追踪间隔i
r11u为r1第一单程的上行列车线,r11d为r1第一单程的下行列车线
r12u为r1第二单程的上行列车线,r12d为r1第二单程的下行列车线
r31u为r3的上行列车线,r31d为r3的下行列车线
其中下标(0)、(1)表示周期数,上下行分别编号
应用列车连接算法,可以获得一个完整周期的列车线接续序列,如
r11u(0)→r11d(0)→r12u(1)→r12d(1)→r31u(2)→r31d(2)→r11u(4)
将该路径的所需时间记为r11u的全周转时间t11u
同理,有r12u,r31u的全周转时间t12u,t31u
总车底数为
五、优选折返方案
使用上述铺点和连接算法,可以尝试得出在各δ参数下,是否有可行的列车线连接方式,以及在可行的δ下,各列车线的接续序列以及折返时间。有可能很多δ都能成功连接,下面说明如何确定较优的δ。
以所需车底数尽可能少且各折返点的余量尽可能小的原则。
5.1所需车底数尽可能少
对各δ计算所需的车底数,只保留车底数最少的可行方案。
5.2各折返点的余量尽可能小
对于每个交路的每个折返点,定义折返余量如下
如图6所示,考虑车站a
t11a折为交路r1在车站a的折返时间
t11a发到为交路r1在车站a的发到间隔
ta最小折为站台a▲的最小折返时间
ta最小发到为站台a▲的最小发到间隔
t11a中点=(t11a折+t11a发到-ta最小折-ta最小发到)/2
t11a余量=|t11a中点-(t11a折-ta最小折)|
总余量=t11a余量+t21c余量+t22c余量+t11b余量+t21d余量+t22d余量。
选择总余量最小的方案作为最终铺画方案。
本领域技术人员可以理解的是,以上是以交路r1以车站a作为折返点举例说明,交路r1的其他折返点以及其他交路的其他折返点折返方案参考上述方法。
以上所述,仅为本发明的具体实施方式,但本发明的保护范围并不局限于此,熟悉该本领域的技术人员应该明白本发明包括但不限于上面具体实施方式中描述的内容。任何不偏离本发明的功能和结构原理的修改都将包括在权利要求书的范围中。
起点商标作为专业知识产权交易平台,可以帮助大家解决很多问题,如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】 与客服一对一沟通,为大家解决相关问题。
与客服一对一沟通,为大家解决相关问题。
此文章来源于网络,如有侵权,请联系删除
 热门咨询
热门咨询



 商标分类
商标分类  商标转让
商标转让 


