基于矩阵表征的高铁网络延误传播定量分析方法与流程

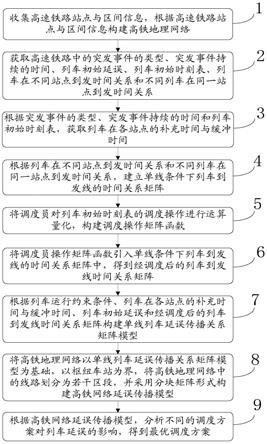
[0001]
本发明涉及延误传播分析技术领域，特别涉及一种基于矩阵表征的高铁网络延误传播定量分析方法。


背景技术：

[0002]
随着我国高铁行业的飞速发展和旅客出行需求的持续增加，随之产生的列车晚点问题也越来越受到人们的关注。研究表明，列车延误会随着列车、线路等媒介在高铁网络中进行类似多米诺效应的传播。同时，对于不同的时段、线路，延误传播的效果不尽相同。因此，探寻延误在高铁系统中的传播机制，了解延误传播特点，以及给出合理的调度策略抑制延误传播成为相关铁路部门亟需解决的问题。
[0003]
在突发事件下，高速铁路应急处置的关键在于调度员能否及时、有效地做出调度决策。现有调度员大多仅凭经验进行调度。当线路情况复杂或突发事件影响范围较大时，调度员的工作量将大量增加，决策效率将大大降低。通过本发明提出的基于调度度量的高速铁路列车延误传播分析方法，可以快速、有效地估算不同调度决策下的延误影响，辅助调度员做出最优调度决策。
[0004]
目前，国内外学者对不同初始延误分布情况下的列车延误传播进行了系统的分析，但没有考虑调度员的调度操作对列车延误传播的直接影响，且对于调度操作的量化分析鲜有研究。


技术实现要素：

[0005]
本发明提供了一种基于矩阵表征的高铁网络延误传播定量分析方法，其目的是为了解决现有研究方法不能直接有效地从调度操作角度为调度员提供建议，无法体现延误动态传播过程中，不同调度操作对延误传播的不同效果的问题。
[0006]
为了达到上述目的，本发明的实施例提供了一种基于矩阵表征的高铁网络延误传播定量分析方法，包括：
[0007]
步骤1，收集高速铁路站点与区间信息，根据高速铁路站点与区间信息构建高铁地理网络；
[0008]
步骤2，获取高速铁路中的突发事件的类型、突发事件持续的时间、列车初始延误、列车初始时刻表、列车在不同站点到发时间关系和不同列车在同一站点到发时间关系；
[0009]
步骤3，根据突发事件的类型、突发事件持续的时间和列车初始时刻表，获取列车在各站点的补充时间与缓冲时间；
[0010]
步骤4，根据列车在不同站点到发时间关系和不同列车在同一站点到发时间关系，建立单线条件下列车到发线的时间关系矩阵；
[0011]
步骤5，将调度员对列车初始时刻表的调度操作进行运算量化，构建调度操作矩阵函数；
[0012]
步骤6，将调度员操作矩阵函数引入单线条件下列车到发线的时间关系矩阵中，得
到经调度后的列车到发线时间关系矩阵；
[0013]
步骤7，根据列车运行约束条件、列车在各站点的补充时间与缓冲时间、列车初始延误和经调度后的列车到发线时间关系矩阵构建单线列车延误传播关系矩阵模型；
[0014]
步骤8，将高铁地理网络以单线列车延误传播关系矩阵模型为基础，以枢纽车站为界，将高铁地理网络中的线路划分为若干区段，并采用分块矩阵形式构建高铁网络延误传播模型；
[0015]
步骤9，根据高铁网络延误传播模型，分析不同的调度方案对列车延误的影响，得到最优调度方案。
[0016]
其中，所述步骤2具体包括：
[0017]
列车初始延误为：
[0018][0019]
其中，表示列车t
k
在站点i的初始延误，表示列车t
k
在站点i的实际发车时间，表示列车t
k
在站点i的计划发车时间,k＝1,2,
…
,n；i＝1,2,
…
,m。
[0020]
其中，所述步骤3具体包括：
[0021]
列车在各站点的补充时间表示为：
[0022][0023][0024][0025]
其中，表示列车t
k
在站点i-1和站点i间的补充时间，表示列车t
k
的区间运行补充时间，表示列车t
k
的停站补充时间，表示列车t
k
计划到达站点i-1的时间，表示列车t
k
计划到达站点i的时间；表示列车t
k
在站点i-1的计划出发时间，表示列车t
k
在站点i的最小停车时间,k＝1,2,
…
,n；i＝1,2,
…
,m；
[0026]
列车在各站点的缓冲时间表示为：
[0027][0028]
其中，表示在站点i列车t
k-1
与列车t
k
间的缓冲时间，表示列车t
k-1
在站点i的出发时间,表示列车t
k
在站点i的出发时间，表示在站点i列车t
k-1
与列车t
k
间的最小间隔时间,k＝2,3,
…
,n；i＝1,2,
…
,m。
[0029]
其中，所述步骤4具体包括：
[0030]
列车运行约束条件：
[0031]
考虑时刻表约束，在实际的列车运行中，考虑到旅客外部因素，列车的实际发车时间不能早于列车的计划发车时间：
[0032]
d(m,n)-y(m,n)≥0
ꢀꢀꢀ
(6)
[0033]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，y(m,n)表示列车在站点的计划发车时间矩阵，m表示高铁运行线路中的总站点数，n表示高铁运行线路中的总列车数；
[0034]
考虑列车运行约束，根据列车运行速度与停站时间的限制，得到列车在区间的运
行约束与列车在站点的运行约束：
[0035]
d(m,n)-w(m,n)-e(m,n)≥0
ꢀꢀꢀ
(7)
[0036]
w(m,n)-d(m-1,n)-r(m-1,n)≥0
ꢀꢀꢀ
(8)
[0037]
其中，w(m,n)表示列车到达站点的时间矩阵，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，e(m,n)表示列车在站点的最小停车时间矩阵；
[0038]
考虑列车之间的间隔约束，在列车的实际运行中，两列车之间的时间间隔应始终大于最小安全间隔：
[0039]
d(m,n)-t[d(m,n-1)]≥t[l(m,n-1)]
ꢀꢀꢀ
(9)
[0040]
其中，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵；
[0041]
考虑车站容量约束，在同一时刻，停站列车的数量不能超过站点的停车股道数量：
[0042][0043]
其中，表示列车t
k
在站点i的实际发车时间，表示列车t
z
到达站点i的时间，t表示所有列车的集合，c
i
表示站点i的停车股道数，sgn(
·
)表示符号函数
[0044]
其中，所述步骤4具体包括：
[0045][0046]
其中，τ(m,n)表示单线列车延误传播关系矩阵，表示列车t
k
在站点i的初始延误，k＝1,2,
…
,n；i＝1,2,
…
,m；
[0047][0048]
其中，u(m-1,n)表示列车在两站点间的补充时间矩阵，表示列车t
k
在站点i-1和站点i间的补充时间，k＝1,2,
…
,n；i＝2,3,
…
,m；
[0049][0050]
其中，b(m,n-1)表示两列车在同一站点的缓冲时间矩阵，表示列车t
k-1
与列车t
k
在站点i的缓冲时间，k＝2,3,
…
,n；i＝1,2,
…
,m；
[0051][0052]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，表示列车t
k
在站点i的实际发车时间，t
k
表示列车信息，i表示站点信息，k＝1,2,
…
,n；i＝1,2,
…
,m,当列车t
k
没有经过站点i时，当列车t
k
经过站点i没有停站或站点i为列车终点站时，列车t
k
在站点i的到达时间约等于列车的发车时间；
[0053][0054]
其中，ε表示负无穷，表示列车t
k
在站点i-1的实际发车时间，k＝1,2,
…
,n；i＝2,3,
…
,m；
[0055][0056]
其中，表示列车t
k-1
在站点i的实际发车时间，k＝2,3,
…
,n；i＝1,2,
…
,m；
[0057][0058]
其中，y(m,n)表示列车在站点的计划发车时间矩阵，表示列车t
k
在站点i的计划发车时间，k＝1,2,
…
,n；i＝1,2,
…
,m；
[0059][0060]
其中，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，表示列车t
k
从站点i-1到站点i的最小运行时间,k＝1,2,
…
,n；i＝2,3,
…
,m；
[0061]
[0062]
其中，e(m,n)表示列车在站点的最小停车时间矩阵，表示列车t
k
在站点i的最小停车时间,k＝1,2,
…
,n；i＝1,2,
…
,m；
[0063][0064]
其中，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵，列车t
k-1
与列车t
k
在站点i的最小发车间隔时间,k＝2,3,
…
,n；i＝1,2,
…
,m；
[0065][0066]
其中，w(m,n)表示列车到达站点的时间矩阵，表示列车t
k
到达站点i的时间；
[0067]
根据列车在不同站点到发时间关系和不同列车在同一站点到发时间关系，建立单线条件下列车到发线的时间关系矩阵：
[0068][0069]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，y(m,n)表示列车在站点的计划发车时间矩阵，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，e(m,n)表示列车在站点的最小停车时间矩阵，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵，m表示高铁运行线路中的总站点数，n表示高铁运行线路中的总列车数。
[0070]
其中，所述步骤5具体包括：
[0071]
将调度员对列车初始时刻表的调度操作进行量化后，构建的调度员操作矩阵函数为：
[0072]
o[x]＝x+t
α
x[α,β]q
1
t
β-t
α
x[α,β]t
β
+p
1
ꢀꢀꢀ
(23)
[0073]
t[x]＝x+t
α
x[α,β]q
2
t
β-t
α
x[α,β]t
β
+p
2
ꢀꢀꢀ
(24)
[0074]
其中，x[α,β]表示提取矩阵x的α行和β列构成的子矩阵，α与β表示提取的行列集合，q
1
与q
2
为初等变换矩阵，表示列车是否在站点超车的调度操作，p
1
和p
2
表示修正矩阵，p
1
、p
2
修正矩阵保证调度操作符合列车运行约束条件。
[0075]
其中，所述步骤6具体包括：
[0076]
将调度员操作矩阵函数引入单线条件下列车到发线的时间关系矩阵中，得到经调度后的列车到发线时间关系矩阵：
[0077][0078]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，y(m,n)表示列车在站点的计划发车时间矩阵，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，e(m-1,n)表示列车在站点的最小停车时间矩阵，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵，m表示高铁运行线路中的总站点数，n表示高铁运行线路中的总列车数。
[0079]
其中，所述步骤7具体包括：
[0080]
根据列车运行约束条件、列车在各站点的补充时间与缓冲时间、列车初始延误和经调度后的列车到发线时间关系矩阵构建单线列车延误传播关系矩阵模型，采用极大代数法表示单线列车延误传播关系矩阵模型：
[0081][0082][0083]
其中，a、b、a和b表示参数，x表示行，y表示列；
[0084][0085]
其中，τ(m,n)表示单线列车延误传播关系矩阵，u(m-1,n)表示列车在两站点间的补充时间矩阵，b(m,n-1)表示两列车在同一站点的缓冲时间矩阵。
[0086]
其中，所述步骤8具体包括：
[0087]
将高铁地理网络以单线列车延误传播关系矩阵模型为基础，以枢纽车站为界，将高铁地理网络中的线路划分为若干区段，并采用分块矩阵形式构建高铁网络延误传播模型：
[0088][0089]
其中，τ(m
1
,n
1
)、τ(m
2
,n
2
)、
…
、τ(m
s
,n
s
)分别表示各路段的延误矩阵，s表示路段。
[0090]
其中，所述步骤9具体包括：
[0091]
通过将调度员操作矩阵函数中的参数α、参数β、初等变换矩阵q
1
，初等变换矩阵q2，修正矩阵p
1
和修正矩阵p
2
进行不同的设定，且分析在同一突发事件下，不同的调度方案对列车延误的影响，得到最优调度方案。
[0092]
本发明的上述方案有如下的有益效果：
[0093]
本发明的上述实施例所述的基于矩阵表征的高铁网络延误传播定量分析方法，将高铁网络延误传播过程通过分块矩阵的形式进行定量分析，量化了列车延误传播过程和调度员的调度操作，有效地从调度操作角度为调度员提供建议，定量分析了延误动态传播过程中，不同调度操作对列车延误动态传播的不同效果。
附图说明
[0094]
图1为本发明的流程图；
[0095]
图2为本发明的上海铁路局管辖范围内的高铁网络图；
[0096]
图3为本发明的列车初始时刻表预留补充时间示意图；
[0097]
图4为本发明的列车初始时刻表预留缓冲时间示意图；
[0098]
图5为本发明的计划时刻表下的列车运行示意图；
[0099]
图6为本发明基于先到先发方案调度的时刻表下的列车运行示意图；
[0100]
图7为本发明基于总延误时间最小方案调度的时刻表下的列车运行示意图；
[0101]
图8为本发明的不同调度方案下各站点的延误分布图。
具体实施方式
[0102]
为使本发明要解决的技术问题、技术方案和优点更加清楚，下面将结合附图及具体实施例进行详细描述。
[0103]
本发明针对现有的研究方法不能直接有效地从调度操作角度为调度员提供建议，无法体现延误动态传播过程中，不同调度操作对延误传播的不同效果的问题，提供了一种基于矩阵表征的高铁网络延误传播定量分析方法。
[0104]
如图1至图8所示，本发明的实施例提供了一种基于矩阵表征的高铁网络延误传播定量分析方法，包括：步骤1，收集高速铁路站点与区间信息，根据高速铁路站点与区间信息构建高铁地理网络；步骤2，获取高速铁路中的突发事件的类型、突发事件持续的时间、列车初始延误、列车初始时刻表、列车在不同站点到发时间关系和不同列车在同一站点到发时间关系；步骤3，根据突发事件的类型、突发事件持续的时间和列车初始时刻表，获取列车在各站点的补充时间与缓冲时间；步骤4，根据列车在不同站点到发时间关系和不同列车在同一站点到发时间关系，建立单线条件下列车到发线的时间关系矩阵；步骤5，将调度员对列车初始时刻表的调度操作进行运算量化，构建调度操作矩阵函数；步骤6，将调度员操作矩阵函数引入单线条件下列车到发线的时间关系矩阵中，得到经调度后的列车到发线时间关系矩阵；步骤7，根据列车运行约束条件、列车在各站点的补充时间与缓冲时间、列车初始延误和经调度后的列车到发线时间关系矩阵构建单线列车延误传播关系矩阵模型；步骤8，将高铁地理网络以单线列车延误传播关系矩阵模型为基础，以枢纽车站为界，将高铁地理网络中的线路划分为若干区段，并采用分块矩阵形式构建高铁网络延误传播模型；步骤9，根据高铁网络延误传播模型，分析不同的调度方案对列车延误的影响，得到最优调度方案。
[0105]
其中，所述步骤2具体包括：列车初始延误为：
[0106][0107]
其中，表示列车t
k
在站点i的初始延误，表示列车t
k
在站点i的实际发车时间，表示列车t
k
在站点i的计划发车时间,k＝1,2,
…
,n；i＝1,2,
…
,m。
[0108]
其中，所述步骤3具体包括：列车在各站点的补充时间表示为：
[0109][0110][0111][0112]
其中，表示列车t
k
在站点i-1和站点i间的补充时间，表示列车t
k
的区间运行补充时间，表示列车t
k
的停站补充时间，表示列车t
k
计划到达站点i-1的时间，表示列车t
k
计划到达站点i的时间；表示列车t
k
在站点i-1的计划出发时间，表示列车t
k
在站点i的最小停车时间,k＝1,2,
…
,n；i＝1,2,
…
,m；
[0113]
列车在各站点的缓冲时间表示为：
[0114][0115]
其中，表示在站点i列车t
k-1
与列车t
k
间的缓冲时间，表示列车t
k-1
在站点i
的出发时间,表示列车t
k
在站点i的出发时间，表示在站点i列车t
k-1
与列车t
k
间的最小间隔时间,k＝2,3,
…
,n；i＝1,2,
…
,m。
[0116]
其中，所述步骤4具体包括：列车运行约束条件：
[0117]
考虑时刻表约束，在实际的列车运行中，考虑到旅客外部因素，列车的实际发车时间不能早于列车的计划发车时间：
[0118]
d(m,n)-y(m,n)≥0
ꢀꢀꢀ
(6)
[0119]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，y(m,n)表示列车在站点的计划发车时间矩阵，m表示高铁运行线路中的总站点数，n表示高铁运行线路中的总列车数；
[0120]
考虑列车运行约束，根据列车运行速度与停站时间的限制，得到列车在区间的运行约束与列车在站点的运行约束：
[0121]
d(m,n)-w(m,n)-e(m,n)≥0
ꢀꢀꢀ
(7)
[0122]
w(m,n)-d(m-1,n)-r(m-1,n)≥0
ꢀꢀꢀ
(8)
[0123]
其中，w(m,n)表示列车到达站点的时间矩阵，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，e(m,n)表示列车在站点的最小停车时间矩阵；
[0124]
考虑列车之间的间隔约束，在列车的实际运行中，两列车之间的时间间隔应始终大于最小安全间隔：
[0125]
d(m,n)-t[d(m,n-1)]≥t[l(m,n-1)]
ꢀꢀꢀ
(9)
[0126]
其中，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵；
[0127]
考虑车站容量约束，在同一时刻，停站列车的数量不能超过站点的停车股道数量：
[0128][0129]
其中，表示列车t
k
在站点i的实际发车时间，表示列车t
z
到达站点i的时间，t表示所有列车的集合，c
i
表示站点i的停车股道数，sgn(
·
)表示符号函数
[0130]
其中，所述步骤4具体包括：
[0131][0132]
其中，τ(m,n)表示单线列车延误传播关系矩阵，表示列车t
k
在站点i的初始延误，k＝1,2,
…
,n；i＝1,2,
…
,m；
[0133]
[0134]
其中，u(m-1,n)表示列车在两站点间的补充时间矩阵，表示列车t
k
在站点i-1和站点i间的补充时间，k＝1,2,
…
,n；i＝2,3,
…
,m；
[0135][0136]
其中，b(m,n-1)表示两列车在同一站点的缓冲时间矩阵，表示列车t
k-1
与列车t
k
在站点i的缓冲时间，k＝2,3,
…
,n；i＝1,2,
…
,m；
[0137][0138]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，表示列车t
k
在站点i的实际发车时间，t
k
表示列车信息，i表示站点信息，k＝1,2,
…
,n；i＝1,2,
…
,m,当列车t
k
没有经过站点i时，当列车t
k
经过站点i没有停站或站点i为列车终点站时，列车t
k
在站点i的到达时间约等于列车的发车时间；
[0139][0140]
其中，ε表示负无穷，表示列车t
k
在站点i-1的实际发车时间，k＝1,2,
…
,n；i＝2,3,
…
,m；
[0141][0142]
其中，表示列车t
k-1
在站点i的实际发车时间，k＝2,3,
…
,n；i＝1,2,
…
,m；
[0143][0144]
其中，y(m,n)表示列车在站点的计划发车时间矩阵，表示列车t
k
在站点i的计划发车时间，k＝1,2,
…
,n；i＝1,2,
…
,m；
[0145][0146]
其中，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，表示列车t
k
从站点i-1到站点i的最小运行时间,k＝1,2,
…
,n；i＝2,3,
…
,m；
[0147][0148]
其中，e(m,n)表示列车在站点的最小停车时间矩阵，表示列车t
k
在站点i的最小停车时间,k＝1,2,
…
,n；i＝1,2,
…
,m；
[0149][0150]
其中，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵，列车t
k-1
与列车t
k
在站点i的最小发车间隔时间,k＝2,3,
…
,n；i＝1,2,
…
,m；
[0151][0152]
其中，w(m,n)表示列车到达站点的时间矩阵，表示列车t
k
到达站点i的时间；
[0153]
根据列车在不同站点到发时间关系和不同列车在同一站点到发时间关系，建立单线条件下列车到发线的时间关系矩阵：
[0154][0155]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，y(m,n)表示列车在站点的计划发车时间矩阵，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，e(m,n)表示列车在站点的最小停车时间矩阵，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵，m表示高铁运行线路中的总站点数，n表示高铁运行线路中的总列车数。
[0156]
其中，所述步骤5具体包括：将调度员对列车初始时刻表的调度操作进行量化后，构建的调度员操作矩阵函数为：
[0157]
o[x]＝x+t
α
x[α,β]q
1
t
β-t
α
x[α,β]t
β
+p
1
ꢀꢀꢀ
(23)
[0158]
t[x]＝x+t
α
x[α,β]q
2
t
β-t
α
x[α,β]t
β
+p
2
ꢀꢀꢀ
(24)
[0159]
其中，x[α,β]表示提取矩阵x的α行和β列构成的子矩阵，α与β表示提取的行列集合，q
1
与q
2
为初等变换矩阵，表示列车是否在站点超车的调度操作，p
1
和p
2
表示修正矩阵，p
1
、
p
2
修正矩阵保证调度操作符合列车运行约束条件。
[0160]
本发明的上述实施例所述的基于矩阵表征的高铁网络延误传播定量分析方法，调度员操作矩阵函数能够量化调度员的具体调度操作，如重新调整列车到发线时间和发车次序，矩阵t
α
与t
β
的每行、每列至多只有一个元素为1，其余全为0，目的是对提取的子矩阵x[α,β]进行扩维，保证子矩阵与矩阵x在同一维度下进行运算。
[0161]
其中，所述步骤6具体包括：将调度员操作矩阵函数引入单线条件下列车到发线的时间关系矩阵中，得到经调度后的列车到发线时间关系矩阵：
[0162][0163]
其中，d(m,n)表示列车在站点的实际发车时间矩阵，y(m,n)表示列车在站点的计划发车时间矩阵，r(m-1,n)表示列车在两个站点之间的最小运行时间矩阵，e(m-1,n)表示列车在站点的最小停车时间矩阵，l(m,n-1)表示列车在站点的最小发车间隔时间矩阵，m表示高铁运行线路中的总站点数，n表示高铁运行线路中的总列车数。
[0164]
本发明的上述实施例所述的基于矩阵表征的高铁网络延误传播定量分析方法，将调度员操作矩阵函数引入单线条件下列车到发线的时间关系矩阵中，给出不同调度方案与列车延误时间和延误范围等重要参数的显式解析关系，调度员操作矩阵函数能够量化调度员的具体调度操作，可以重新调整列车的到发线时间和列车的发车次序。
[0165]
其中，所述步骤7具体包括：根据列车运行约束条件、列车在各站点的补充时间与缓冲时间、列车初始延误和经调度后的列车到发线时间关系矩阵构建单线列车延误传播关系矩阵模型，采用极大代数法表示单线列车延误传播关系矩阵模型：
[0166][0167][0168]
其中，a、b、a和b表示参数，x表示行，y表示列；
[0169][0170]
其中，τ(m,n)表示单线列车延误传播关系矩阵，u(m-1,n)表示列车在两站点间的补充时间矩阵，b(m,n-1)表示两列车在同一站点的缓冲时间矩阵。
[0171]
其中，所述步骤8具体包括：将高铁地理网络以单线列车延误传播关系矩阵模型为基础，以枢纽车站为界，将高铁地理网络中的线路划分为若干区段，并采用分块矩阵形式构建高铁网络延误传播模型：
[0172][0173]
其中，τ(m
1
,n
1
)、τ(m
2
,n
2
)、
…
、τ(m
s
,n
s
)分别表示各路段的延误矩阵，s表示路段。
[0174]
其中，所述步骤9具体包括：通过将调度员操作矩阵函数中的参数α、参数β、初等变换矩阵q
1
，初等变换矩阵q2，修正矩阵p
1
和修正矩阵p
2
进行不同的设定，且分析在同一突发事件下，不同的调度方案对列车延误的影响，得到最优调度方案。
[0175]
本发明的上述实施例所述的基于矩阵表征的高铁网络延误传播定量分析方法，通
过收集高速铁路站点与区间信息构建高铁地理网络，通过获取的高速铁路中的突发事件的类型、突发事件持续的时间、列车初始延误、列车初始时刻表、列车在不同站点到发时间关系和不同列车在同一站点到发时间关系得知列车在各站点的补充时间与缓冲时间，通过列车在不同站点到发时间关系和不同列车在同一站点到发时间关系，建立单线条件下列车到发线的时间关系矩阵；通过将调度员对列车初始时刻表的调度操作进行运算量化，构建调度操作矩阵函数，并将调度员操作矩阵函数引入单线条件下列车到发线的时间关系矩阵中，得到经调度后的列车到发线时间关系矩阵，且根据列车运行约束条件、列车在各站点的补充时间与缓冲时间、列车初始延误和经调度后的列车到发线时间关系矩阵构建单线列车延误传播关系矩阵模型，将高铁地理网络以单线列车延误传播关系矩阵模型为基础，以枢纽车站为界，将高铁地理网络中的线路划分为若干区段，并采用分块矩阵形式构建高铁网络延误传播模型，基于高铁网络延误传播模型，分析不同的调度方案对列车延误的影响，得出最优调度方案。
[0176]
本发明的上述实施例所述的基于矩阵表征的高铁网络延误传播定量分析方法，从矩阵角度考虑高铁网络中的列车延误，建立高铁网络延误传播模型，将列车延误传播过程和调度员的调度操作过程用数值矩阵表示，量化了列车延误传播过程和调度员的调度操作；所述基于矩阵表征的高铁网络延误传播定量分析方法构建的高铁网络延误传播模型，通过调整调度员操作矩阵函数，可以快速、有效地估算不同调度方案下的延误影响，辅助调度员做出最优调度方案决策，所述基于矩阵表征的高铁网络延误传播定量分析方法操作过程简单，整体时间复杂度低，适用于处理大范围的高铁网络，从调度操作角度有效地为调度员提供建议，充分体现了列车延误传播过程中，不同的调度操作对列车延误传播产生的不同的影响。
[0177]
以上所述是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明所述原理的前提下，还可以作出若干改进和润饰，这些改进和润饰也应视为本发明的保护范围。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除