一种基于纵向安全距离的车辆换道决策方法与流程

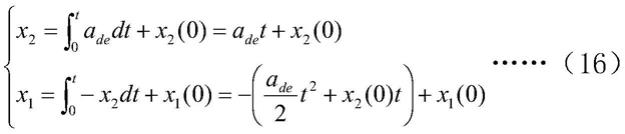
[0001]
本发明涉及汽车高级驾驶辅助系统技术领域，具体为一种基于纵向安全距离的车辆换道决策方法。


背景技术：

[0002]
随着人们对车辆行驶安全性和舒适性要求越来越高，智能车辆控制系统逐渐成为研究热点。换道辅助系统作为一种典型的主动安全系统，是智能车辆控制系统的重要组成部分。
[0003]
换道行为集智能车辆的感知，决策，规划和执行为一体，首先由传感器(激光雷达，毫米波雷达，相机等)检测车辆运动状态和行驶环境信息，经过决策层判断目标操作，之后规划出一条与周围车辆和其他障碍物均不发生碰撞的换道期望轨迹，最后执行换道操作。由换道产生的交通事故占总交通事故的比例不高，但其会严重降低运输效率，将很大程度上影响道路的流通性。


技术实现要素：

[0004]
本发明的目的在于提供一种基于纵向安全距离的车辆换道决策方法，以解决上述背景技术中提出的问题。
[0005]
为了解决上述技术问题，本发明提供如下技术方案：一种基于纵向安全距离的车辆换道决策方法，包括以下步骤：步骤一，建立模型；步骤二，调整换道；
[0006]
其中在上述步骤一中，根据换道车辆换道过程速度变化规律，建立换道车辆与本车道前车、目标车道前车不发生碰撞的最小纵向安全距离模型；
[0007]
其中在上述步骤二中，根据采集的信息结合安全距离模型判断是否满足安全换道条件，不满足时进行纵向速度调整直至满足安全换道条件再进行换道，对调整策略下的换道时刻进行求解，并进行验证。
[0008]
根据上述技术方案，所述步骤二中，信息是由毫米波雷达和激光雷达进行采集。
[0009]
根据上述技术方案，所述步骤二中，验证方式是通过matlab仿真验证纵向速度调整策略的可行性。
[0010]
与现有技术相比，本发明所达到的有益效果是：该一种基于纵向安全距离的车辆换道决策方法，本发明提出的简单纵向速度调整策略可有效应对车辆与周围环境之间不满足安全换道条件的情况，通过简单的匀加速运动或匀速运动调节车辆之间的相对距离来构造安全换道情景，在实际道路行驶中具有很强的应用意义。
附图说明
[0011]
附图用来提供对本发明的进一步理解，并且构成说明书的一部分，与本发明的实施例一起用于解释本发明，并不构成对本发明的限制。在附图中：
[0012]
图1和图2均为换道发生碰撞示意图；
[0013]
图3为本发明的换道决策流程示意图；
[0014]
图4为本发明的换道安全区域分界图；
[0015]
图5和图6均为本发明的纵向速度调整仿真图；
[0016]
图7是本发明的方法流程图。
具体实施方式
[0017]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0018]
请参阅图1-7，本发明提供一种技术方案：一种基于纵向安全距离的车辆换道决策方法，包括以下步骤：步骤一，建立模型；步骤二，调整换道；
[0019]
其中在上述步骤一中，根据换道车辆换道过程速度变化规律，建立换道车辆与本车道前车、目标车道前车不发生碰撞的最小纵向安全距离模型；以单向直线双车道换道过程为例，建立换道初始时刻换道车辆m与目标车道前车l
d
，初始车道前车l
0
之间的纵向安全距离模型，以保证换道过程中及换道完成后m与l
d
,l
0
不发生任何形式的碰撞,定义坐标系xoy表示换道过程中各车的位置坐标，ox轴正向沿车辆纵向行驶方向，oy轴正向由初始车道指向目标车道，坐标原点o为换道车辆靠近目标车道的侧边线上任一点，定义各车位置坐标即为车辆前保险杠左端点在xoy系中的坐标，x
i
(t),y
i
(t)分别为第i辆车t时刻的横坐标，纵坐标；v
i
,a
i
表示第i辆车t时刻x方向速度，x方向加速度；l
i
,w
i
为第i辆车长度，宽度，且i＝l
d
,l
0
m；
[0020]
1)换道车辆与目标车道前车l
d
最小纵向安全距离，考虑换道车辆与目标车道前车将要发生碰撞的临界情况如图1，图1中c点为换道车辆前保险杠左端点,ls与目标车道上前车靠近初始车道的侧边线相切,设m在t＝0时刻开始换道，在t＝t
c
时刻c点到达ls线，在t＝t
all
时刻完成换道，分析换道过程可知，在c点到达ls线至换道完成时间段内即t∈[t
c
,t
all
],两车可能发生碰撞，设m在换道过程中t时刻的横摆角为θ(t)，为满足换道过程中不发生碰撞，则对应有：
[0021][0022]
为简化问题，显然在t∈[t
c
,t
all
]，sin(θ(t))单减，则有：
[0023]
max(sin(θ(t)))＝sin(θ(t
c
))
……
(2)
[0024]
当t＝t
c
时，有：
[0025][0026]
在已知换道横向运动位移随时间变化规律下，由公式(3)可求得t
c
,若使公式(4)公式成立，则公式(1)必然成立,其中：
[0027][0028]
[0029]
令则：
[0030][0031]
即对公式(6)成立可保证换道中l
d
与m不发生碰撞；
[0032]
2)换道车辆与初始车道前车最小纵向安全距离，考虑换道车辆与目标车道前车将要发生碰撞的临界情况如图2，图2中c点为换道车辆后保险杠左端点,ls与目标车道前车靠近初始车道的侧边线相切,设m在t＝0时刻开始换道，在t＝t
c
时刻c点到达ls线，在t＝t
all
时刻完成换道，同上，分析换道过程可知，在c点到达ls线至换道完成时间段即t∈[t
c
,t
all
]，两车可能发生碰撞，设m在换道过程中t时刻的横摆角为θ(t)，为满足换道过程中l
0
与m不发生碰撞，则对应有：
[0033][0034]
为简化问题，显然在t∈[0,t
c
]，sin(θ(t))单增，则有：
[0035]
max(sin(θ(t)))＝sin(θ(t
c
))
……
(8)
[0036]
当t＝t
c
时，有：
[0037][0038]
在已知换道横向运动位移随时间变化规律下，由公式(9)可求得t
c
,对若使公式(10)成立，则公式(7)必然成立,则有：
[0039][0040]
根据位移计算公式，则：
[0041][0042]
令则：
[0043][0044]
即对公式(12)成立可保证换道中l
0
与m不发生碰撞；
[0045]
其中在上述步骤二中，根据采集的信息结合安全距离模型判断是否满足安全换道条件，且信息是由毫米波雷达和激光雷达进行采集，不满足时进行纵向速度调整直至满足安全换道条件再进行换道，对调整策略下的换道时刻进行求解，并进行验证，且验证方式是通过matlab仿真验证纵向速度调整策略的可行性；结合利用毫米波雷达和激光雷达探测的m与目标车道前车l
d
，初始车道前车l
0
之间的实际相对距离和相对速度，做出是否换道的决策，换道决策流程图如图3，由于在不满足最小安全距离条件下调整换道车辆的速度方法多种多样，且需要根据邻近车辆运动状态来调整，过于复杂，因此，本专利只举例说明当道路上仅有l
d
和m时，为满足最小安全距离条件，m可采取的调整纵向速度简单策略即匀加速或匀减速或匀速，假设l
d
在目标车道上匀速行驶，速度为v
ld
，m在t＝0调整纵向速度，加速度为
常量a
m
，到换道完成即t＝t
all
时使得结合公式(6)可得：
[0046][0047]
进一步分类讨论得：
[0048][0049]
假设t
all
＝5s,t
c
＝2.5s，以为横轴，以s
1
(0)为纵轴，利用matlab作得安全区域/不安全区域如图4，当l
d
与m的相对距离和相对速度落在安全区域时，可进行安全换道；落在不安全区域时，可通过简单的速度调整来达到安全换道的目的；下面通过matlab建立两种仿真工况，验证恒定加速度，恒定速度策略的有效性；
[0050]
1)当v
m
(0)＞v
ld
时，取s
1
(0)＝10m，显然未调整m车速前，l
d
与m的纵向距离不够，且m保持匀速或匀加速都不会满足最小安全纵向距离要求，考虑使m从t＝0开始匀减速至t＝t
1
，减速度为a
de
，令，令则：
[0051][0052]
故：
[0053][0054]
对(16)下式进行等价转化得：
[0055][0056]
分别取加速度a
de
＝-2m/s
2
，a
de
＝-3.2m/s
2
，a
de
＝-4m/s
2
，以x
2
为横轴，x
1
为纵轴，用matlab联立x
1-x
2
表达式方程和安全区域/不安全区域分界线方程，使用fsolve函数求解联立方程组的解，得到位于安全区域/不安全区域分界线上x
1
和x
2
的解，作匀减速速度调整策略下换道车辆由不安全区域向安全区域过渡的仿真变化图如图5，根据图5可知，当换道车辆m初始时刻速度大于目标车道前车l
d
的速度且初始时刻纵向换道距离不足时，m可采取匀减速的速度调整策略，随着时间增加，减小，相对应时刻的(x
2
,x
1
)按图中箭头方向沿x
1-x
2
曲线移动，当到达x
1-x
2
曲线与安全区域与不安全区域的分界线的交点时，满足最小
安全纵向距离要求，此时开始换道，可使l
d
与m不发生碰撞，当换道车辆m以a
de
＝-4m/s
2
进行速度调整时，可以以最短的时间调整相对距离至满足安全换道条件；
[0057]
2)当时，取s
1
(0)＝-15m，这种情况下，换道车辆m初始时刻速度小于目标车道前车l
d
的速度，且初始时刻纵向换道距离不足，可以采取两种速度调整策略；一种是换道车辆m采取匀减速的速度调整策略，另一种策略是换道车辆m保持当前行驶速度不变，这两种策略都会使换道车辆m和目标车道前车l
d
的相对纵向距离增加，考虑一种简单仿真情况，m保持车速不变直至(x
2
,x
1
)到达安全区域，同样以x
2
为横轴，x
1
为纵轴，用matlab联立x
1-x
2
表达式方程和安全区域/不安全区域分界线方程，使用fsolve函数求解联立方程组的解，得到位于安全区域/不安全区域分界线上x
1
和x
2
的解，作匀速速度调整策略下换道车辆由不安全区域向安全区域过渡的仿真变化图如图6，根据图6可知，随着时间增加，对应时刻的(x
2
,x
1
)按图中箭头方向沿x
1-x
2
曲线移动，当到达x
1-x
2
曲线与安全区域与不安全区域的分界线的交点时，满足最小安全纵向距离要求，换道车辆m此时开始换道，可使l
d
与m不发生碰撞。
[0058]
基于上述，本发明的优点在于，本发明，实际换道决策判断中，一方面，结合换道速度规划和轨迹规划可以得到最小纵向安全距离模型参数t
c
,t
all
，进而确定换道安全区域/不安全区域分界线，另一方面，毫米波雷达可实时采集前方道路一定角度范围内车辆的相对速度和相对距离，激光雷达实时采集的点云信息通过聚类或深度学习的算法可以得到一定范围内行驶车辆的车身尺寸大小，通过这两种传感器就可以获取x
1
＝x
ld-x
m-l
1
和x
2
＝v
m-v
ld
的实际数值，当检测到x
1-x
2
初始条件落在安全区域时，换道车辆m可执行换道操作；当检测到初始条件落在不安全区域时，根据实际情况确定速度调整策略即恒定加速度的大小，得到x
1-x
2
变化关系方程，作出一段时间内x
1-x
2
变化关系曲线，求x
1-x
2
变化关系曲线与换道安全区域/不安全区域分界线的交点，此交点对应的时刻即为速度调整后满足安全换道条件的时刻，求解这两条曲线交点的过程实质是求解非线性方程零点的问题，利用matlab的fslove函数可得到换道决策结果，利用该发明，在实际道路行驶中具有很强的应用意义。
[0059]
需要说明的是，在本文中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。
[0060]
最后应说明的是：以上所述仅为本发明的优选实施例而已，并不用于限制本发明，尽管参照前述实施例对本发明进行了详细的说明，对于本领域的技术人员来说，其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。

起点商标作为专业知识产权交易平台，可以帮助大家解决很多问题，如果大家想要了解更多知产交易信息请点击 【在线咨询】或添加微信 【19522093243】与客服一对一沟通，为大家解决相关问题。

此文章来源于网络,如有侵权,请联系删除